非线性系统：相平面法

非线性系统的相平面法是一种重要的分析工具，用于研究系统的动力学行为。通过相平面法，可以直观地观察系统状态变量的变化，分析系统的稳定性、周期性和其他动力学特性。本文将详细介绍相平面法的基本思想、步骤、相轨迹的绘制方法，探讨线性系统与非线性系统的相平面分析，并提供一个非线性系统的程序示例，最后讨论相平面法的优缺点。

基本思想

相平面法通过将系统的状态变量表示在一个二维平面上，并绘制出这些变量随时间变化的轨迹，以揭示系统的动力学特性。相平面法可以帮助我们理解系统的稳定性、周期性行为、极限环等特性。

相平面法步骤

相平面法的基本步骤如下：

建立系统的微分方程 ：

对于一个二阶非线性系统，其微分方程可以表示为：
x ¨ = f ( x , x ˙ ) \ddot{x} = f(x, \dot{x}) x¨=f(x,x˙)
转换为一阶微分方程组 ：

将二阶微分方程转换为两个一阶微分方程：
{ x ˙ = y y ˙ = f ( x , y ) \begin{cases} \dot{x} = y \\ \dot{y} = f(x, y) \end{cases} {x˙=yy˙=f(x,y)
数值求解微分方程 ：

使用数值方法（如 Runge-Kutta 法）求解微分方程组，得到状态变量随时间的演化。
绘制相平面和相轨迹 ：

在相平面上绘制状态变量之间的关系，形成相轨迹。

相轨迹绘制方法

Python 实现相平面和相轨迹绘制

以下是一个简单的 Python 示例，展示了如何绘制 Van der Pol 振荡器的相平面和相轨迹。

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

def van_der_pol(t, z, mu):
    x, y = z
    dxdt = y
    dydt = mu * (1 - x**2) * y - x
    return [dxdt, dydt]

# 参数
mu = 1.0
t_span = (0, 100)
y0 = [1, 0]

# 求解微分方程
sol = solve_ivp(van_der_pol, t_span, y0, args=(mu,), dense_output=True)

# 绘制相平面和相轨迹
t = np.linspace(0, 100, 4000)
z = sol.sol(t)
x, y = z

plt.plot(x, y, label='Van der Pol oscillator')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Phase Plane of Van der Pol Oscillator')
plt.legend()
plt.grid(True)
plt.show()

在上述代码中，我们定义了 Van der Pol 振荡器的微分方程，并使用 solve_ivp 函数求解该方程。然后，我们在相平面上绘制出系统的相轨迹。

线性系统的相平面分析

线性系统的相平面分析是一种经典方法，用于研究线性微分方程的动力学行为。通过分析系统的特征值，可以判断系统的稳定性。

对于一个二阶线性系统，其状态方程可以表示为：
x ˙ = A x \dot{\mathbf{x}} = A\mathbf{x} x˙=Ax

其中， x = [ x 1 , x 2 ] T \mathbf{x} = [x_1, x_2]^T x=[x1,x2]T 是状态向量， A A A 是系统矩阵。

系统矩阵 A A A 的特征值决定了系统在相平面上的行为：

如果特征值均为负实数，系统趋于稳定的平衡点。
如果特征值有正实数，系统是不稳定的。
如果特征值为复数且实部为负，系统表现出稳定的螺旋轨迹。
如果特征值为复数且实部为正，系统表现出不稳定的螺旋轨迹。

线性系统的相平面绘制示例

python 复制代码

import numpy as np
import matplotlib.pyplot as plt

# 定义线性系统
A = np.array([[0, 1], [-2, -3]])

# 求解特征值和特征向量
eigvals, eigvecs = np.linalg.eig(A)

# 绘制特征向量
origin = np.array([[0, 0], [0, 0]])
fig, ax = plt.subplots()
ax.quiver(*origin, eigvecs[0,:], eigvecs[1,:], color=['r','b'], scale=5)

# 设置坐标轴
ax.axhline(0, color='black',linewidth=0.5)
ax.axvline(0, color='black',linewidth=0.5)
ax.grid(color = 'gray', linestyle = '--', linewidth = 0.5)

plt.xlim(-2, 2)
plt.ylim(-2, 2)
plt.title('Phase Plane of Linear System')
plt.xlabel('x1')
plt.ylabel('x2')
plt.show()

非线性系统的相平面分析

非线性系统的相平面分析比线性系统复杂得多，因为非线性系统的动力学行为更加多样化。通过相平面法，可以直观地观察非线性系统的复杂行为，如极限环、混沌等。

示例：Van der Pol 振荡器

Van der Pol 振荡器是一个经典的非线性系统，其动力学方程为：
{ x ˙ = y y ˙ = μ ( 1 − x 2 ) y − x \begin{cases} \dot{x} = y \\ \dot{y} = \mu (1 - x^2) y - x \end{cases} {x˙=yy˙=μ(1−x2)y−x

通过数值求解和绘制相轨迹，可以观察其在相平面上的动力学行为。

Python 实现

python 复制代码

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

def van_der_pol(t, z, mu):
    x, y = z
    dxdt = y
    dydt = mu * (1 - x**2) * y - x
    return [dxdt, dydt]

# 参数
mu = 1.0
t_span = (0, 100)
y0 = [1, 0]

# 求解微分方程
sol = solve_ivp(van_der_pol, t_span, y0, args=(mu,), dense_output=True)

# 绘制相平面和相轨迹
t = np.linspace(0, 100, 4000)
z = sol.sol(t)
x, y = z

plt.plot(x, y, label='Van der Pol oscillator')
plt.xlabel('x')
plt.ylabel('y')
plt.title('Phase Plane of Van der Pol Oscillator')
plt.legend()
plt.grid(True)
plt.show()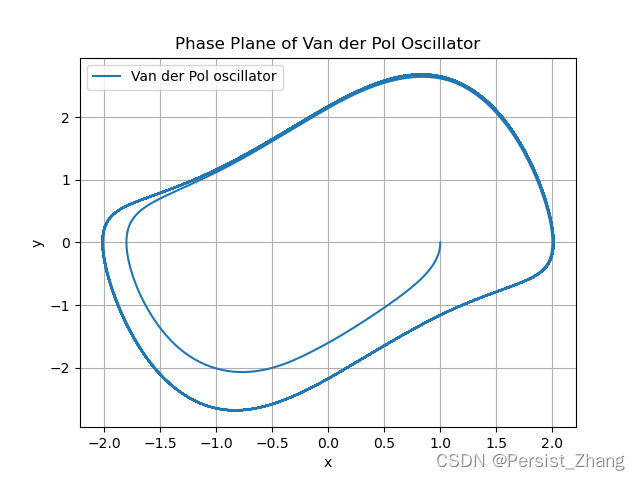

优缺点

优点

直观性：相平面法通过可视化的方式展示系统的状态变化，直观地揭示系统的动力学特性。
分析稳定性：通过分析相轨迹，可以判断系统的平衡点和稳定性。
揭示周期性行为：相平面法能够识别系统的周期性行为和极限环。

缺点

限于二维系统：相平面法只适用于二维系统，对于高维系统无法直接应用。
无法精确解析求解：相平面法主要是基于图形观察和分析，无法提供精确的定量信息。
可视化有限：对于复杂的相轨迹和相平面，仅凭人眼可能无法完全捕捉到细微的变化和行为特征。
对数值求解的依赖：相平面法通常依赖于数值计算和数值模拟，这涉及到选择适当的数值方法，并对数值误差和数值稳定性有充分的认识。

结论

相平面法是分析非线性系统的重要工具，通过绘制相轨迹，可以直观地观察和理解系统的动力学行为。虽然相平面法有其局限性，但它在揭示系统的稳定性、周期性和极限环等特性方面具有重要作用。希望本文能够帮助您更好地理解相平面法在非线性系统中的应用。如果您有任何问题或建议，欢迎在评论区留言讨论。

推荐两个可以直接绘制相轨迹的网站：

http://mathlets.org/mathlets/linear-phase-portraits-matrix-entry/

http://www.bluffton.edu/homepages/facstaff/nesterd/java/slopefields.html