【Python】【matLab】模拟退火算法求二元高次函数最小值

一、目标函数

求二元高次函数的最小值。目标函数选择：

用于测试算法的简单的目标函数：

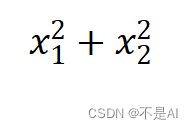
二、Python代码实现

python 复制代码

import numpy as np


# 目标函数（2变量）
def objective_function(x):
    return x[0] ** 2 + 2 * x[0] - 15 + 4 * 4 * 2 * x[1] + 4 * x[1] ** 2
    # 测试：return x[0] ** 2 + x[1] ** 2


# 模拟退火
def simulated_annealing(objective_func,  # 目标函数
                        initial_solution=np.array([0, 0]),  # 初始解
                        temperature=100,  # 初始温度
                        min_temperature=0.1,  # 最小温度值
                        cooling_rate=0.90,  # 冷却率（乘法系数）
                        iter_max=100,  # 最大迭代次数
                        seed=0  # 随机种子
                        ):
    np.random.seed(seed)
    current_solution = initial_solution
    best_solution = current_solution

    while temperature > min_temperature:
        for j in range(iter_max):
            # 生成新的解
            new_solution = current_solution + np.random.uniform(-1, 1, len(current_solution))

            # 计算新解与当前解之间的目标函数值差异
            current_cost = objective_func(current_solution)
            new_cost = objective_func(new_solution)
            cost_diff = new_cost - current_cost

            # 判断是否接受新解
            if cost_diff < 0 or np.exp(-cost_diff / temperature) > np.random.random():
                current_solution = new_solution

            # 更新最优解
            if objective_func(current_solution) < objective_func(best_solution):
                best_solution = current_solution

        # 降低温度
        temperature *= cooling_rate

    return best_solution


# 调用退火算法求解最小值
best_solution = simulated_annealing(objective_function)

print(f"函数最小值： {objective_function(best_solution)} 自变量取值：{best_solution}")

代码参考博客：利用Python 实现模拟退火算法

三、程序输出

测试函数输出：

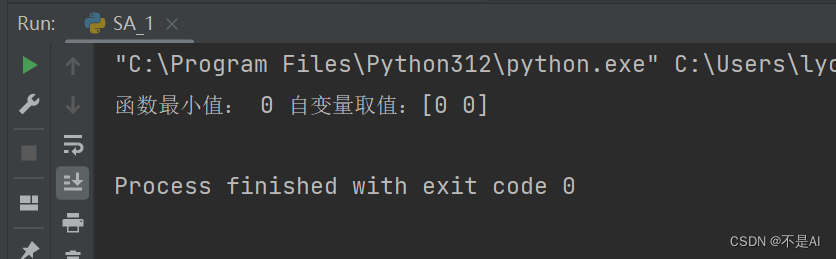
目标函数输出：

四、MatLab验证程序

参考博客：MATLAB求解二元(多元)函数极值

先定义目标函数（位于fun2_3.m中）：

matlab 复制代码

function f = fun2_3(x)
f = x(1) ^ 2 + 2 * x(1) - 15 + 32 * x(2) + 4 * x(2) ^ 2;

模拟退火算法求极值：

matlab 复制代码

clc, clear
[x, y]=meshgrid(-10:0.3:10,-10:0.3:10);
z = x.^2 + 2 * x -15 + 32 * y + 4 * y.^2;
figure(1)
surf(x,y,z)
xlabel('X');
ylabel('Y');
zlabel('Z');

figure(2)
contour(x,y,z)
xlabel('X');
ylabel('Y');
grid on;

x0=[-3,-3];
% [x,fmin]=fminsearch(@fun2_3,x0)
[x,fmin] = fminunc(@fun2_3,x0)

程序输出：

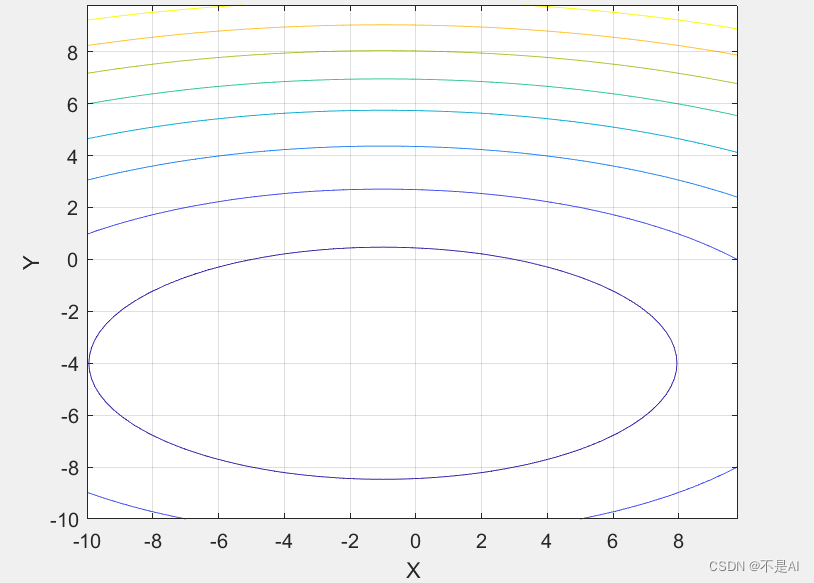
可见，两种方法的求解结果基本相同。