为啥找对象千万别找大厂男，还好我不是大厂的。。

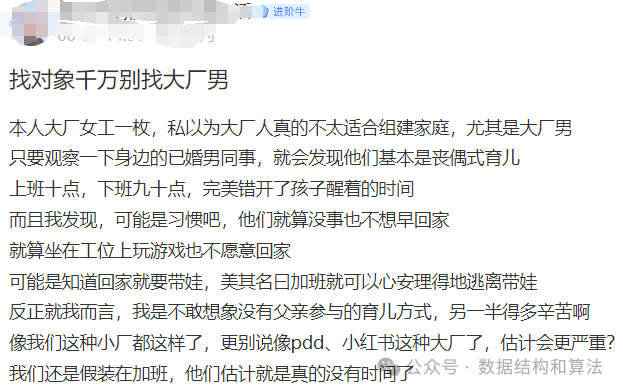
网上看到一大厂女员工发文说：找对象千万别找大厂男，理由说了一大堆，无非就是大厂男为了逃避带娃，以加班为由宁愿在工位上玩游戏也不愿回家。当然这种观点有的人赞同有的人反对。

网友精彩评论：

--------------下面是今天的算法题--------------

来看下今天的算法题，这题是LeetCode的第45题：跳跃游戏 II。

问题描述

来源：LeetCode第45题

难度：中等

给定一个长度为 n 的 0 索引整数数组 nums。初始位置为 nums[0]。每个元素 nums[i] 表示从索引 i 向前跳转的最大长度。换句话说，如果你在 nums[i] 处，你可以跳转到任意 nums[i + j] 处:

1，0 <= j <= nums[i]

2，i + j < n

返回到达 nums[n - 1] 的最小跳跃次数。生成的测试用例可以到达 nums[n - 1]。

示例1：

输入: nums = [2,3,1,1,4]

输出: 2

解释: 跳到最后一个位置的最小跳跃数是 2。
 从下标为 0 跳到下标为 1 的位置，跳 1 步，然后跳 3 步到达数组的最后一个位置。

示例2：

输入: nums = [2,3,0,1,4]

输出: 2

1 <= nums.length <= 10^4
0 <= nums[i] <= 1000
题目保证可以到达 nums[n-1]

问题分析

这题让计算的是跳到数组的最后需要跳跃的最小次数，第一次跳跃是站在下标为0的位置开始跳的。

我们可以用一个变量preRange表示上一次跳跃所能到达的范围，然后在这个范围内记录跳跃所能达到的最远距离curFarthest，计算的时候如果超过preRange这个范围就表示需要再跳一次，然后更新preRange的值为curFarthest。

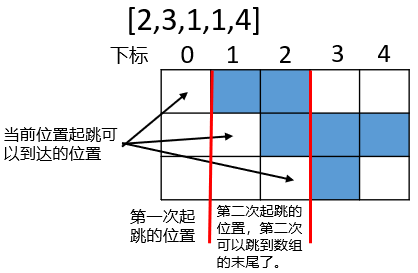
我们以示例一为例画个图来看下，第一次可以跳跃的范围是[1,2]，这里指的是下标，实际上还可以跳到下标为0的位置，如果第一次还跳到下标为0就表示没跳，我们不要记录了。

第二次可以从下标为1或下标为2的位置开始跳，从下标为1的位置可以跳到[2,3,4]，从下标为2的位置可以跳到[3]，所以第二次就可以跳到数组的末尾了，只需要两次即可。

JAVA：

public int jump(int[] nums) {
    int jumps = 0;// 最小跳跃次数
    int preRange = 0;// 上一次起跳的范围
    int curFarthest = 0;// 从上一次起跳范围内所能跳的最远距离。
    for (int i = 0; i < nums.length - 1; i++) {
        // 计算从当前位置跳跃所能到大的最远距离，并更新curFarthest。
        curFarthest = Math.max(curFarthest, i + nums[i]);
        // 如果上一个跳远范围内都计算完了，就要重新开始跳了。
        if (i == preRange) {
            jumps++;
            preRange = curFarthest;
        }
    }
    return jumps;
}

C++：

public:
    int jump(vector<int>& nums) {
        int jumps = 0;// 最小跳跃次数
        int preRange = 0;// 上一次起跳的范围
        int curFarthest = 0;// 从上一次起跳范围内所能跳的最远距离。
        for (int i = 0; i < nums.size() - 1; i++) {
            // 计算从当前位置跳跃所能到大的最远距离，并更新curFarthest。
            curFarthest = max(curFarthest, i + nums[i]);
            // 如果上一个跳远范围内都计算完了，就要重新开始跳了。
            if (i == preRange) {
                jumps++;
                preRange = curFarthest;
            }
        }
        return jumps;
    }

C：

int jump(int *nums, int numsSize) {
    int jumps = 0;// 最小跳跃次数
    int preRange = 0;// 上一次起跳的范围
    int curFarthest = 0;// 从上一次起跳范围内所能跳的最远距离。
    for (int i = 0; i < numsSize - 1; i++) {
        // 计算从当前位置跳跃所能到大的最远距离，并更新curFarthest。
        curFarthest = fmax(curFarthest, i + nums[i]);
        // 如果上一个跳远范围内都计算完了，就要重新开始跳了。
        if (i == preRange) {
            jumps++;
            preRange = curFarthest;
        }
    }
    return jumps;
}

Python：

def jump(self, nums: List[int]) -> int:
    # 最小跳跃次数
    # 上一次起跳的范围
    # 从上一次起跳范围内所能跳的最远距离。
    jumps, preRange, curFarthest = 0, 0, 0
    for i in range(len(nums) - 1):
        # 计算从当前位置跳跃所能到大的最远距离，并更新curFarthest。
        curFarthest = max(curFarthest, i + nums[i])
        # 如果上一个跳远范围内都计算完了，就要重新开始跳了。
        if i == preRange:
            jumps += 1
            preRange = curFarthest
    return jumps