Python数据分析-二手车价格预测分析

一、研究背景

随着我国的机动车数量不断增长，人均保有量也随之增加，机动车以"二手车"形式在流通环节，包括二手车收车、二手车拍卖、二手车零售、二手车置换等环节的流通需求越来越大。二手车作为一种特殊的"电商商品"，因为其"一车一况"的特性比一般电商商品的交易要复杂得多，究其原因是二手车价格难于准确估计和设定，不但受到车本身基础配置，如品牌、车系、动力等的影响，还受到车况如行驶里程、车身受损和维修情况等的影响，甚至新车价格的变化也会对二手车价格带来作用。。。。。

二、实证分析

本文数据共包含3个子数据，分别为估价训练数据，估价验证数据，门店历史交易数据。本文数据都是以txt格式展示，故在后续处理中要注意数据格式。

基于给定的二手车交易样本数据（附件 1：估价训练数据），选用合适的估价方法，构建模型，预测二手车的零售交易价格，数据中会对 id 类，主要特征类等信息进行脱敏。主要数据包括车辆基础信息、交易时间信息、价格信息等，包含 36 列变量信息，其中15 列为匿名变量。字段如下：

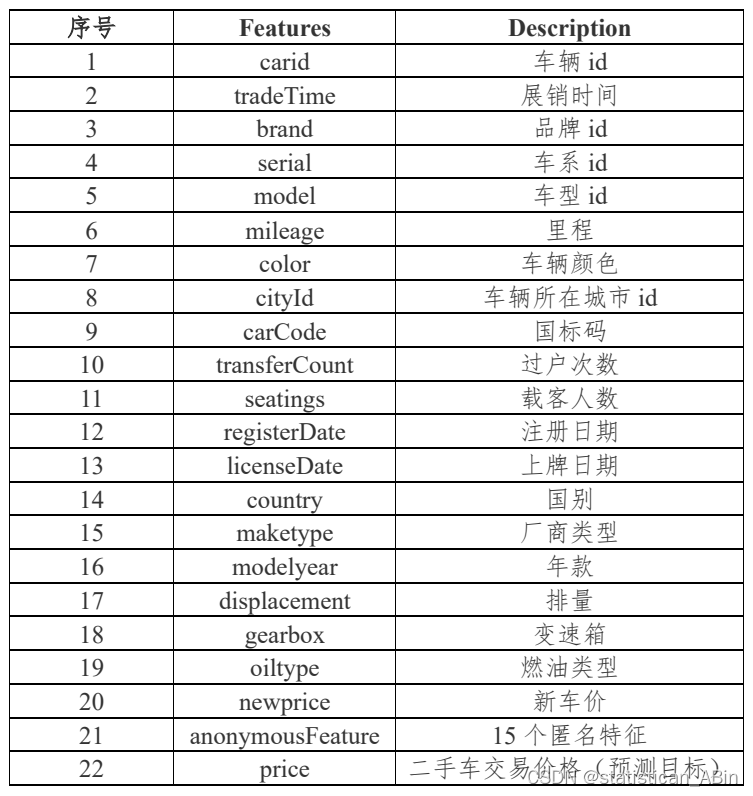
元素数据如下图，由于元素数据为txt格式且没有特征名称，故利用上表所给的特征名称表进行补充并且进行读取和展示数据，同时测试集也如此，展示如下图：

数据和代码

报告代码和数据

python 复制代码

train_data=pd.read_csv('附件1：估价训练数据.txt',sep='\t',header=None,names=columns)

随后对数据的特征变量进行描述性统计（此处只展示训练集的数据），展示结果如下：

从上图中可以看出，对于训练集的描述性统计，对各个特征变量的计数、均值、标准差、最大最小值，以及分位数均进行了展示。随后推断数据类型，让数据更规范以及查看数据的基础信息，结果如下（仍是以训练数据集为例），这一步是为了对数据做预处理做准备。

python 复制代码

train_data.infer_objects()
test_data.infer_objects()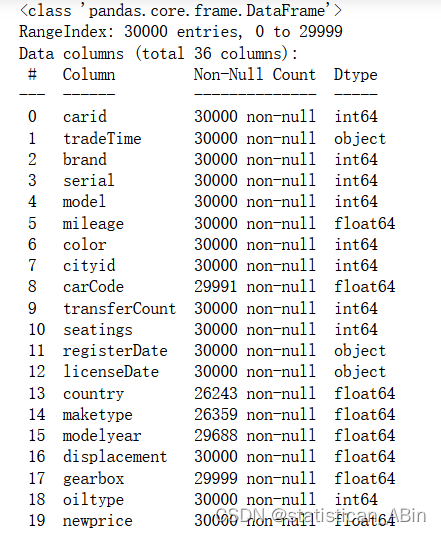

接下来对数据进行预处理，首先导入缺失值可视化missingno包，该包可以很直观的看出每个特征的缺失程度，故可以很好的对特征进行筛选，可视化结果如下，在每个特征中白色越多就表明数据越缺失。

python 复制代码

import missingno as msno
msno.matrix(train_data)

随后，对于缺失程度太大的特征就剔除，特征缺失程度一般的话就填充，填充方法一般由先前填充和向后填充、均值和中位数填充，在本文中是运用的中位数向前填充并且针对数值型特征和非数值型特征数据进行处理，例如进行独热编码等等。

python 复制代码

#缺失到一定比例就删除
miss_ratio=0.15
for col in train_data.columns:
    if  train_data[col].isnull().sum()>train_data.shape[0]*miss_ratio:
        print(col)
        train_data.drop(col,axis=1,inplace=True)

python 复制代码

train_data.fillna(train_data.median(),inplace=True)   #mode,mean
train_data.fillna(method='ffill',inplace=True)   #pad,bfill/backfill
 
test_data.fillna(test_data.median(),inplace=True)   
test_data.fillna(method='ffill',inplace=True)

python 复制代码

#剩下的变量独热处理
train_data=pd.get_dummies(train_data)
test_data=pd.get_dummies(test_data)

python 复制代码

dis_cols = 7                   #一行几个
dis_rows = len(columns)
plt.figure(figsize=(4 * dis_cols, 4 * dis_rows))
 
for i in range(len(columns)):
    plt.subplot(dis_rows,dis_cols,i+1)
    sns.boxplot(data=train_data[columns[i]], orient="v",width=0.5)
    plt.xlabel(columns[i],fontsize = 20)
plt.tight_layout()
#plt.savefig('特征变量箱线图',formate='png',dpi=500)
plt.show()

从图中可以看出仍然存在一些特征存在离群点，在后续进行处理，在图中没有出现箱线图的特征是因为我们对该特征进行了one-hot编码。

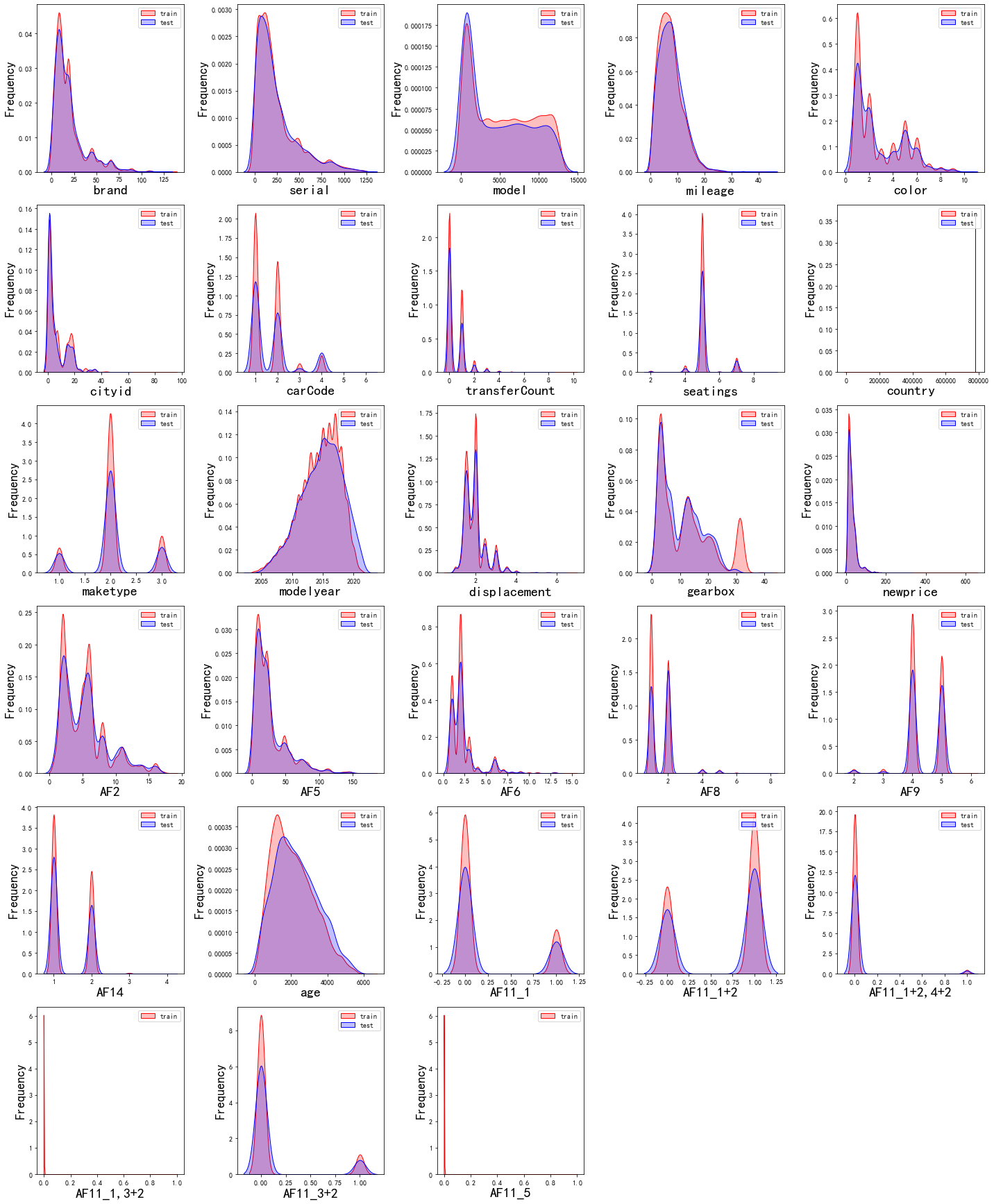
在处理完特征变量之后，对响应变量的分布也要考察，若存在异常值的情况也会对模型的泛化能力有影响，在此画出响应变量的箱线图、直方图和和核密度图，如下图：

python 复制代码

plt.figure(figsize=(6,2),dpi=128)
plt.subplot(1,3,1)
y.plot.box(title='响应变量箱线图')
plt.subplot(1,3,2)
y.plot.hist(title='响应变量直方图')
plt.subplot(1,3,3)
y.plot.kde(title='响应变量核密度图')
#sns.kdeplot(y, color='Red', shade=True)
#plt.savefig('响应变量.png')
plt.tight_layout()
plt.show()

可以从箱线图中看到，该响应变量存在异常值，故我们要对异常值做处理，在本文中，结合数据，我们将响应变量的阈值设为小于200，处理之后的响应变量如下图：

python 复制代码

y=y[y <= 200]
plt.figure(figsize=(6,2),dpi=128)
plt.subplot(1,3,1)
y.plot.box(title='响应变量箱线图')
plt.subplot(1,3,2)
y.plot.hist(title='响应变量直方图')
plt.subplot(1,3,3)
y.plot.kde(title='响应变量核密度图')
#sns.kdeplot(y, color='Red', shade=True)
#plt.savefig('响应变量.png')
plt.tight_layout()
plt.show()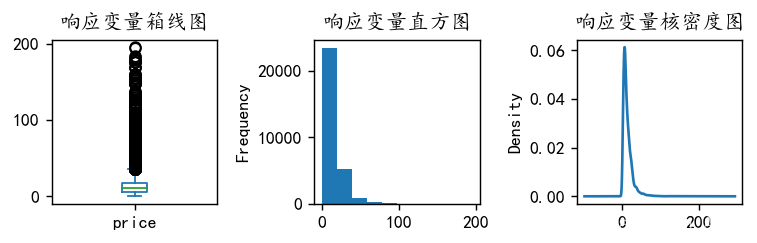

python 复制代码

plt.figure(figsize=(20,8))
plt.boxplot(x=X_s,labels=train_data.columns)
#plt.hlines([-10,10],0,len(columns))
plt.show()

随后对特征变量进行相关系数的计算以及热力图的展示，如下图：

python 复制代码

corr = plt.subplots(figsize = (20,16),dpi=128)
corr= sns.heatmap(train_data.assign(Y=y).corr(method='spearman'),annot=True,square=True)

从图中可以看出每个特征变量之间的相关性。但是我们最关心的是看二手车价格和那个特征变量的相关性更高，从图中可以看出，newprice，也就是新车的价格相关性最高。

在特征工程完成之后，便可进行机器学习：

首先对数据集进行划分，划分为训练集和验证集。本文的划分比例为0.8，随后将数据标准化，训练集、验证集和测试集均如此。。。。

python 复制代码

from sklearn.linear_model import LinearRegression
from sklearn.linear_model import ElasticNet
from sklearn.neighbors import KNeighborsRegressor
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from sklearn.ensemble import GradientBoostingRegressor
from xgboost.sklearn import XGBRegressor
from lightgbm import LGBMRegressor
from sklearn.svm import SVR
from sklearn.neural_network import MLPRegressor

python 复制代码

#线性回归
model1 = LinearRegression()
 
#弹性网回归
model2 = ElasticNet(alpha=0.05, l1_ratio=0.5)
 
#K近邻
model3 = KNeighborsRegressor(n_neighbors=10)
 
#决策树
model4 = DecisionTreeRegressor(random_state=77)
 
#随机森林
model5= RandomForestRegressor(n_estimators=500,  max_features=int(X_train.shape[1]/3) , random_state=0)
 
#梯度提升
model6 = GradientBoostingRegressor(n_estimators=500,random_state=123)
 
#极端梯度提升
model7 =  XGBRegressor(objective='reg:squarederror', n_estimators=1000, random_state=0)
 
#轻量梯度提升
model8 = LGBMRegressor(n_estimators=1000,objective='regression', # 默认是二分类
                      random_state=0)
 
#支持向量机
model9 = SVR(kernel="rbf")
 
#神经网络
model10 = MLPRegressor(hidden_layer_sizes=(16,8), random_state=77, max_iter=10000)
 
model_list=[model1,model2,model3,model4,model5,model6,model7,model8,model9,model10]
model_name=['线性回归','惩罚回归','K近邻','决策树','随机森林','梯度提升','极端梯度提升','轻量梯度提升','支持向量机','神经网络']

线性回归方法在验证集的准确率为：0.7584680526870519

随机森林方法在验证集的准确率为：0.9641697798108289

梯度提升方法在验证集的准确率为：0.9618323536976034

轻量梯度提升方法在验证集的准确率为：0.9705572612616453

支持向量机方法在验证集的准确率为：0.7259004919925829

神经网络方法在验证集的准确率为：0.9318712490163676

交叉验证和对比

python 复制代码

plt.subplots(1,4,figsize=(16,3))
for i,col in enumerate(lgb_crosseval.columns):
    n=int(str('14')+str(i+1))
    plt.subplot(n)
    plt.plot(lgb_crosseval[col], 'k', label='LGB')
    plt.plot(xgb_crosseval[col], 'b-.', label='XGB')
    plt.plot(rf_crosseval[col], 'r-^', label='RF')
    plt.title(f'不同模型的{col}对比')
    plt.xlabel('重复交叉验证次数')
    plt.ylabel(col,fontsize=16)
    plt.legend()
plt.tight_layout()
plt.show()

在对模型进行预测之后，还可以画出其特征变量对二手车价格影响的重要性排序，如下图：

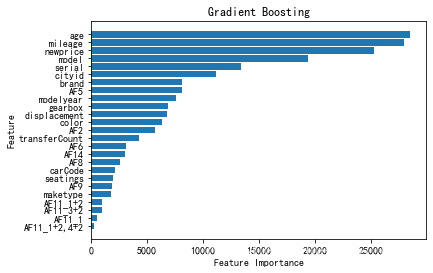
可以看到对二手车价格影响最大的变量是车龄age，车跑的里程数mileage，还有同款新车的价格newprice。

三、结论

轻量梯度提升方法在验证集上表现最佳，可作为预测二手车价格的首选模型。车龄、里程数和同款新车价格是影响二手车价格的最重要因素。进一步提升模型预测能力可通过交叉验证和网格搜索等方法优化模型参数。。。。。

创作不易，希望大家多点赞关注评论！！！（类似代码或报告定制可以私信）