目录
[1. 如何开始数学建模](#1. 如何开始数学建模)
[1.1 选择和描述问题](#1.1 选择和描述问题)
[1.2 提出基本假设](#1.2 提出基本假设)
[1.3 确定模型类型](#1.3 确定模型类型)
[2. 建模的数学基础](#2. 建模的数学基础)
[2.1 线性代数基础](#2.1 线性代数基础)
[2.2 微分方程基础](#2.2 微分方程基础)
[2.3 统计与概率基础](#2.3 统计与概率基础)
[3. 模型的求解方法](#3. 模型的求解方法)
[3.1 解析法](#3.1 解析法)
[3.2 数值法](#3.2 数值法)
[3.3 近似法](#3.3 近似法)
[4. 案例分析与实战演练](#4. 案例分析与实战演练)
[4.1 问题识别和界定](#4.1 问题识别和界定)
[4.2 提出基本假设](#4.2 提出基本假设)
[4.3 模型的建立](#4.3 模型的建立)
[4.4 模型的求解与实现](#4.4 模型的求解与实现)
[4.5 结果验证与分析](#4.5 结果验证与分析)
[4.6 模型优化与改进](#4.6 模型优化与改进)
引言
在上一篇文章中,我们概述了数学建模的基本概念和重要性。本篇文章将详细讲解从零开始进行数学建模的过程,涵盖问题选择、假设提出、模型建立和求解的各个环节。通过具体的案例分析和代码示例,帮助读者掌握基础的建模技巧,迈出数学建模的第一步。
1. 如何开始数学建模
1.1 选择和描述问题
选择一个适合建模的问题至关重要。对于初学者,选择一个相对简单、明确且易于理解的问题有助于更快入门。例如,可以选择研究城市交通流量、环境污染扩散或股票价格波动等问题。
示例问题:研究城市某路口的交通流量,并优化信号灯的设置以减少等待时间。
1.2 提出基本假设
为了简化实际问题并使之可以数学化,需要提出一些合理的假设。这些假设应基于对问题基本特性的了解。
示例假设:
- 假设车辆按照一定速度匀速行驶。
- 车流量在观察期间恒定。
- 车辆遵守交通信号,不发生交通事故。
1.3 确定模型类型
选择合适的模型类型是建模的重要环节。常见的模型类型包括线性模型、非线性模型、动态模型和静态模型等。每种模型类型都有其适用范围和特点。
示例模型:
- 使用排队理论模型来描述车辆在路口的等待时间。
- 使用微分方程模型来描述车流密度和速度的变化。
2. 建模的数学基础
2.1 线性代数基础
矩阵运算
矩阵是描述线性系统的基本工具。常见的矩阵运算包括加法、乘法、转置和求逆等。
示例:矩阵乘法
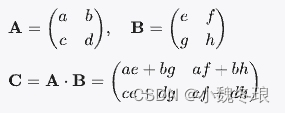
线性方程组的解法
线性方程组是最常见的建模工具之一,常用的求解方法包括高斯消元法和LU分解法等。
示例:求解线性方程组
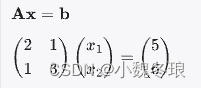
使用Matlab代码求解:
Matlab
A = [2, 1; 1, 3];
b = [5; 6];
x = A \ b;2.2 微分方程基础
常微分方程
常微分方程用于描述动态系统的变化,如人口增长、传染病传播等。
示例:人口增长模型

偏微分方程
偏微分方程用于描述空间和时间上变化的系统,如热传导、流体流动等。
示例:热传导方程

2.3 统计与概率基础
描述性统计
描述性统计用于总结和描述数据的特征,包括均值、中位数、方差和标准差等。
示例:计算均值和方差

概率基础
概率用于描述随机事件发生的可能性,包括常见的概率分布如正态分布、泊松分布等。
示例:正态分布

3. 模型的求解方法
3.1 解析法
解析法是指通过数学推导直接得到模型的解。常见的解析方法包括分离变量法、积分法等。
示例:分离变量法求解微分方程

3.2 数值法
数值法用于求解解析法无法解决的复杂模型。常见的数值方法包括欧拉法、龙格-库塔法、有限差分法等。
示例:欧拉法求解微分方程

3.3 近似法
近似法用于简化复杂问题,使其更易于求解。常见的近似方法包括泰勒级数展开、渐近展开等。
示例:一阶泰勒展开
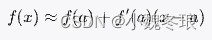
4. 案例分析与实战演练
案例:交通流模型
4.1 问题识别和界定
研究城市某交通路口的车流情况,目标是优化交通信号灯设置以减少车辆的等待时间。
4.2 提出基本假设
- 车辆按照一定速度匀速行驶。
- 车流量在观察期间恒定。
- 车辆遵守交通信号,不发生交通事故。
4.3 模型的建立
使用排队理论模型描述车辆在路口的等待时间:

4.4 模型的求解与实现
Matlab求解示例
Matlab
% Matlab代码示例
lambda = 10; % 车流量
T = 30; % 信号灯时长
L = (lambda^2 * T) / (2 * (1 - lambda * T));
disp(['平均等待时间:', num2str(L), '秒']);4.5 结果验证与分析
将模型得到的结果与实际观测数据进行比对。如果误差较大,可能需要调整模型的参数或假设。例如,可以通过实地数据测量校正车流量参数。
4.6 模型优化与改进
通过调整信号灯的时长,提高车辆的通行效率。可以进行多个不同方案的数值模拟,比较其效果,选择最佳方案。
Matlab
% 优化信号灯时长
best_T = 0;
min_waiting_time = inf;
for T = 10:1:60
L = (lambda^2 * T) / (2 * (1 - lambda * T));
if L < min_waiting_time
min_waiting_time = L;
best_T = T;
end
end
disp(['优化后的最佳信号灯时长:', num2str(best_T), '秒']);结语
通过本篇文章的详细讲解,读者应该了解了从零开始进行数学建模的基本步骤和方法。从问题选择、假设提出到模型建立和求解,这些内容为初学者打下了坚实的基础。
