1-AI带你认识TOPSIS
📘 一、TOPSIS 方法简介
1. 基本定义:
TOPSIS(Technique for Order Preference by Similarity to an Ideal Solution),中文通常称为:
• 优劣解距离法
• 逼近理想解排序法
• 理想点法
它是一种经典的多指标综合评价方法 ,由 C.L. Hwang 和 K. Yoon 于 1981 年提出 ,主要用于解决多方案、多指标的综合排序与优选问题。
2. 核心思想:
TOPSIS 的核心思想是:通过计算每个评价对象与"理想解"(最优方案)和"负理想解"(最劣方案)之间的距离,来对各个方案进行优劣排序;距离"理想解"越近、距离"负理想解"越远的方案,其综合评价结果越好。
简单来说就是:
• 先找出所有对象中每个指标的最好值(正理想解) 和 最差值(负理想解)
• 然后计算每个方案到这两个理想点的距离
• 最后根据接近最优、远离最劣的程度 进行排序,距离最优最近、最劣最远的方案最优
🧩 二、TOPSIS 方法的基本步骤
下面是 TOPSIS 方法的标准操作流程(非常规范、清晰,适合建模与论文使用):
步骤 1:构建原始决策矩阵
假设有 m 个评价对象(如方案、城市、企业等) ,n 个评价指标,构建初始数据矩阵:
X=x11x21⋮xm1x12x22⋮xm2⋯⋯⋱⋯x1nx2n⋮xmn其中 xij表示第 i个对象在第 j个指标上的原始取值。
步骤 2:数据标准化处理
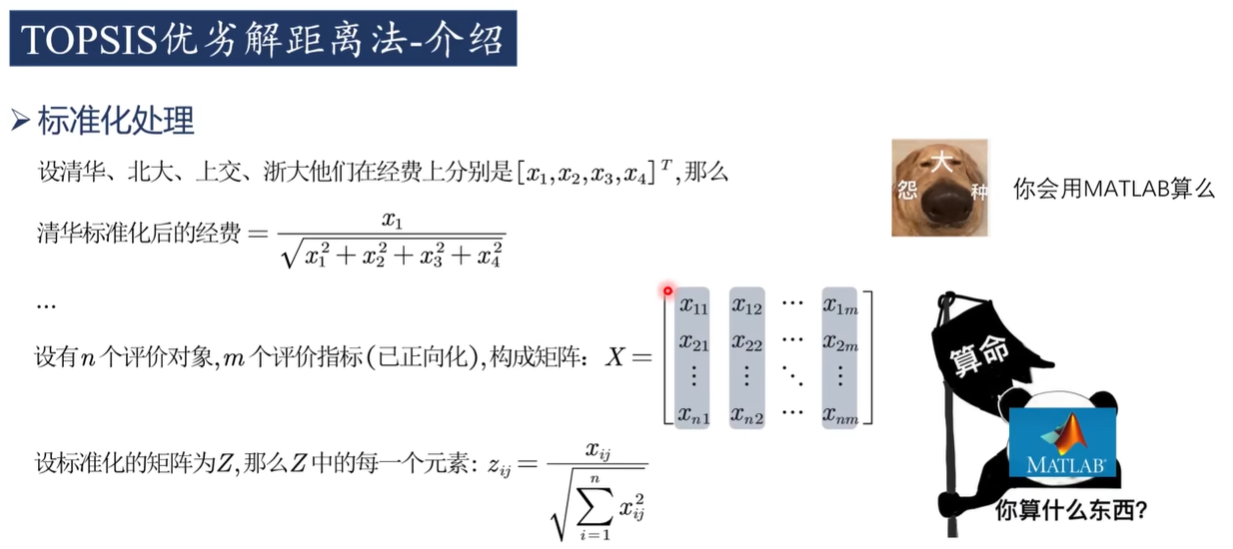
由于不同指标可能具有不同的量纲(单位)、数量级,需要对原始数据进行标准化(归一化)处理,消除量纲影响,常用方法为:
(1)向量归一化(常用):
yij=∑i=1mxij2xij或者(2)极差标准化(区分正向/负向指标):
• 正向指标(越大越好):
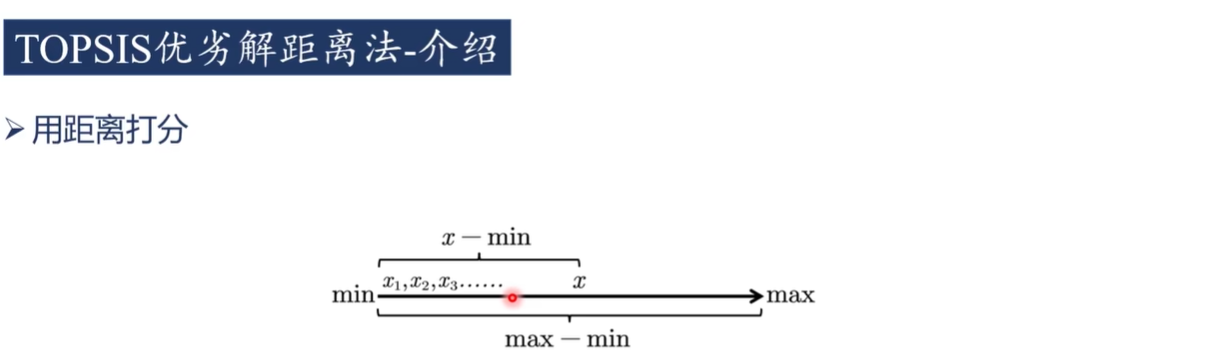
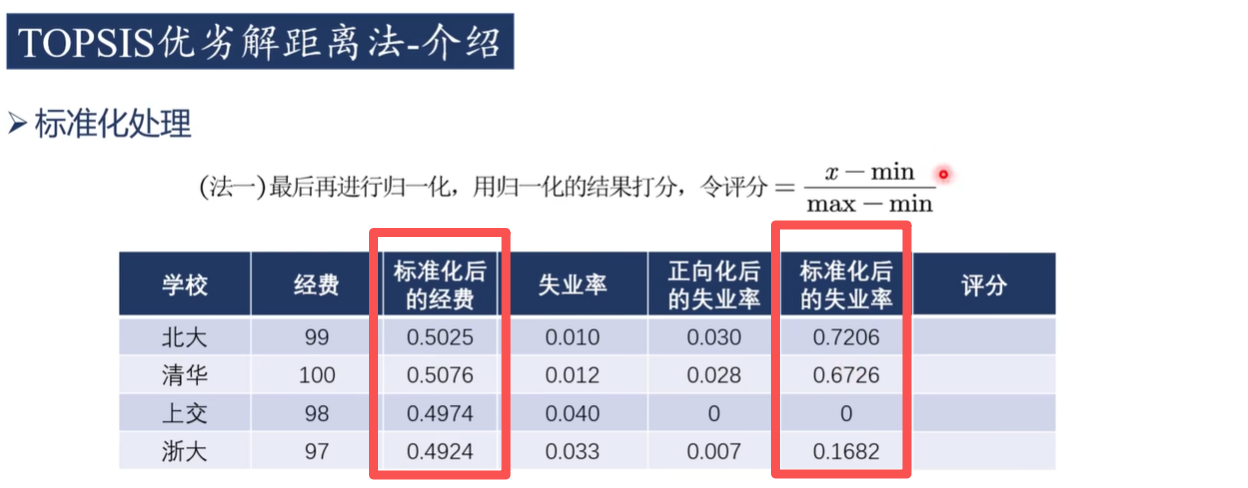
yij=max(xj)−min(xj)xij−min(xj)
• 负向指标(越小越好):
yij=max(xj)−min(xj)max(xj)−xij标准化后得到矩阵 Y=(yij)m×n,其中各元素 yij∈[0,1]
步骤 3:确定加权标准化矩阵(可选)
如果各指标的重要性不同,可以引入权重 wj(如通过 AHP、熵权法等方法获得),构造加权标准化决策矩阵:
V=(vij)m×n,vij=wj⋅yij其中 wj是第 j 个指标的权重,且满足 ∑j=1nwj=1
✅ 在实际应用中,TOPSIS 往往会结合主观或客观权重方法使用,使评价更加科学合理。
步骤 4:确定正理想解和负理想解
• 正理想解(最优解) V+:每个指标取最优值
• 对于 正向指标:取最大值
• 对于 负向指标:取最小值
• 负理想解(最劣解) V−:每个指标取最劣值
• 对于 正向指标:取最小值
• 对于 负向指标:取最大值
具体为:
vj+=max(v1j,v2j,...,vmj)或min(v1j,...,vmj)(根据指标类型)
vj−=min(v1j,v2j,...,vmj)或max(v1j,...,vmj)(根据指标类型)
步骤 5:计算各方案到正、负理想解的距离
• 到正理想解的距离(欧氏距离):
Di+=j=1∑n(vij−vj+)2
• 到负理想解的距离(欧氏距离):
Di−=j=1∑n(vij−vj−)2其中 Di+越小越好,Di−越大越好。
步骤 6:计算相对贴近度(综合得分)
Ci=Di++Di−Di−,0≤Ci≤1
• Ci越接近 1 ,说明该方案越接近最优解、远离最劣解,评价结果越好
• Ci越接近 0,说明该方案越差
步骤 7:排序与决策
• 按照 Ci值从大到小排序
• Ci最大的方案即为最优方案
✅ 三、TOPSIS 方法的优点与缺点
✅ 优点:
- 直观易懂:基于"距离理想解"的思想,逻辑清晰,易于理解与解释
- 适用性广:适用于多指标、多方案的综合评价与排序问题
- 综合正负两方面信息:同时考虑最优和最劣情况,评价更全面
- 结果明确:能给出清晰的方案优劣排序,便于决策
- 可结合权重:常与 AHP、熵权法等结合,使用主观或客观权重,提高科学性
❌ 缺点:
- 对数据标准化方法敏感:不同的标准化方式可能影响结果
- 依赖权重设置:权重的合理性直接影响排序结果
- 仅基于距离度量:未考虑指标之间的相关性等更复杂信息
📚 四、TOPSIS 的应用场景举例
• 方案优选类问题:如选择最优投资方案、供应商、旅游地、城市规划方案等
• 绩效评价类问题:如企业绩效、政府绩效、学校排名、医院服务评价等
• 综合评价类问题:如城市竞争力、环境质量、能源效率、技术创新能力等
• 多指标决策问题:几乎所有涉及多个指标、多个对象优选排序的问题
🧠 五、总结一句话:
TOPSIS(优劣解距离法)是一种基于"距离理想解"思想的多指标综合评价方法,通过计算各评价对象与最优解和最劣解的距离,得到相对贴近度,从而进行排序与优选,是一种直观、科学、应用广泛的决策分析工具。
2-理论知识
介绍

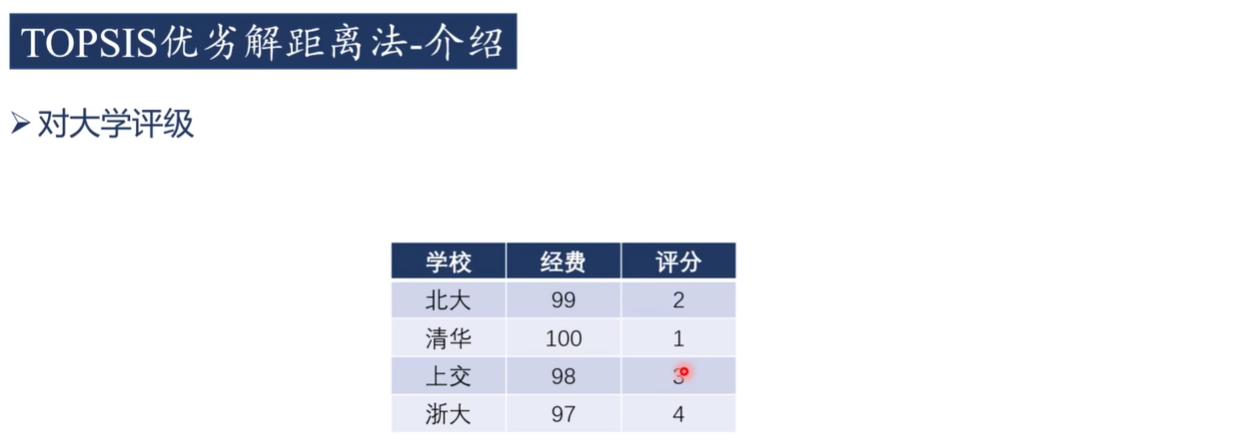
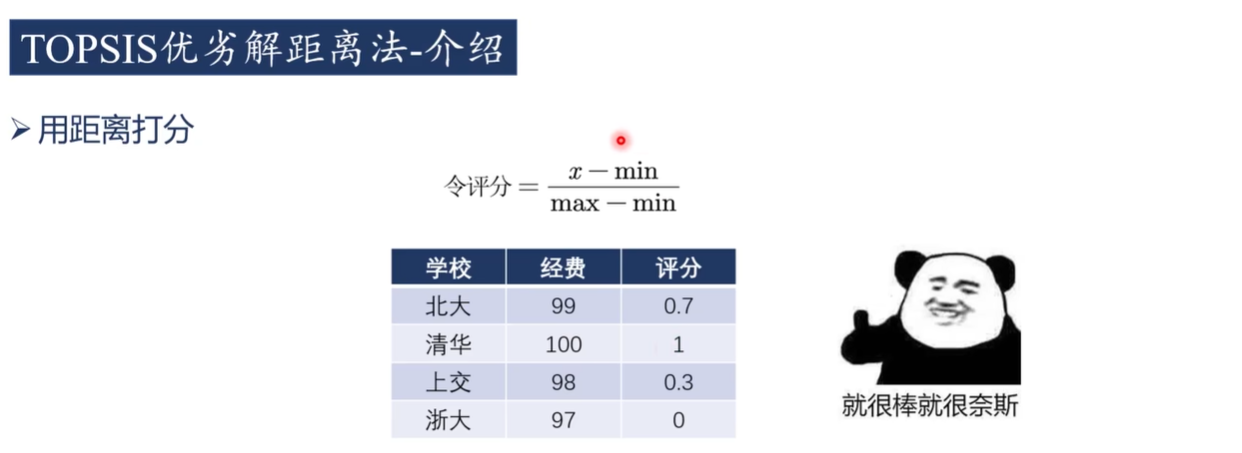

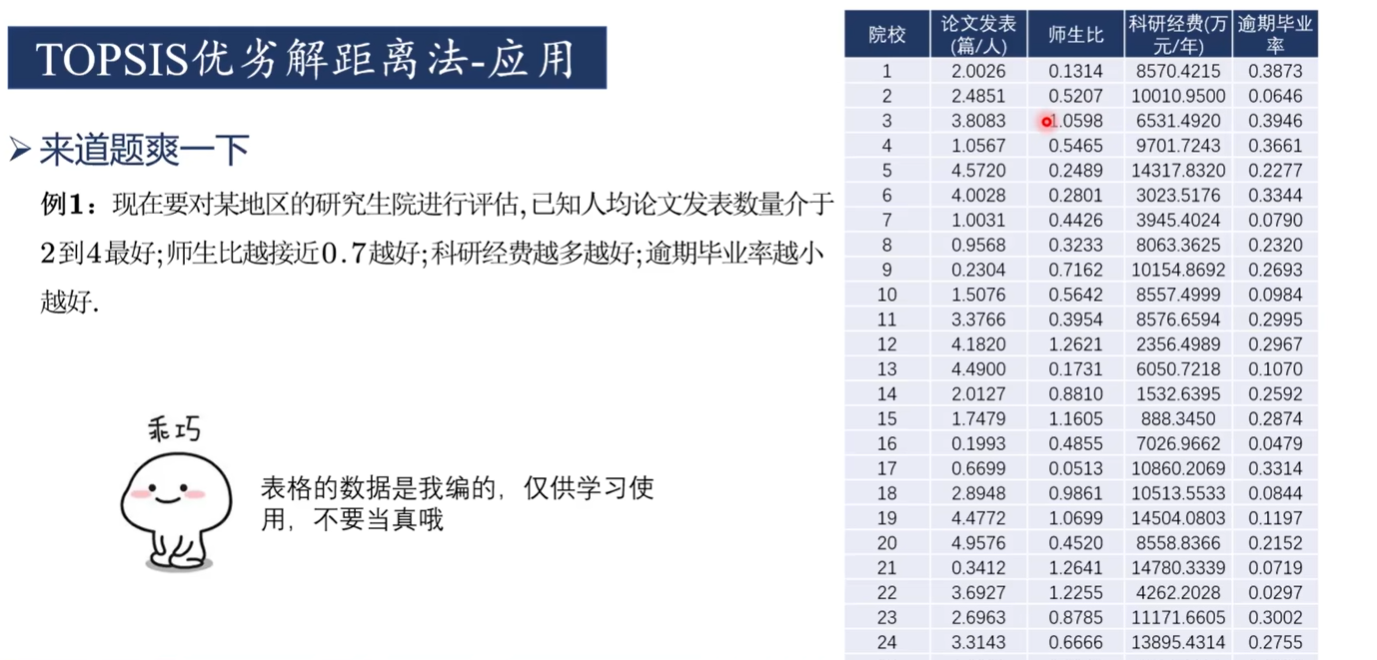
答案:不是

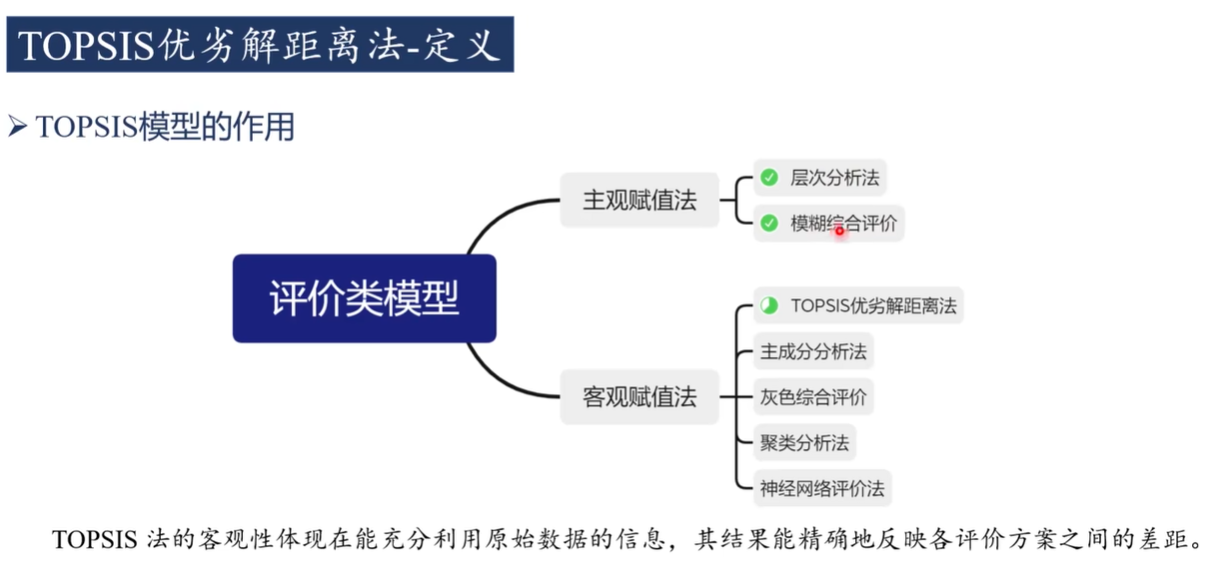
定义

步骤
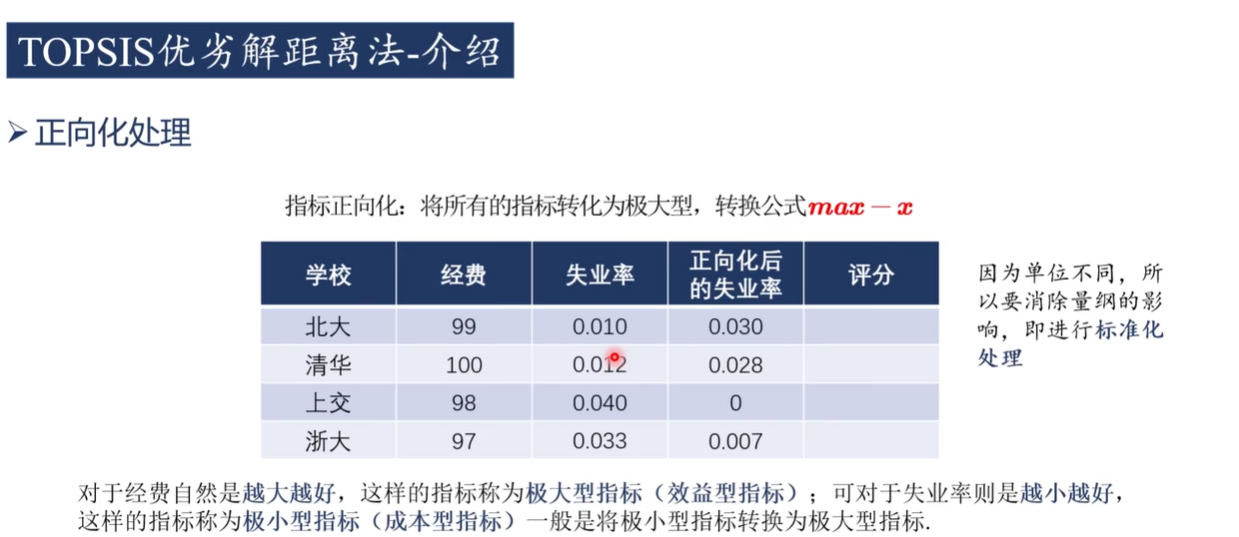
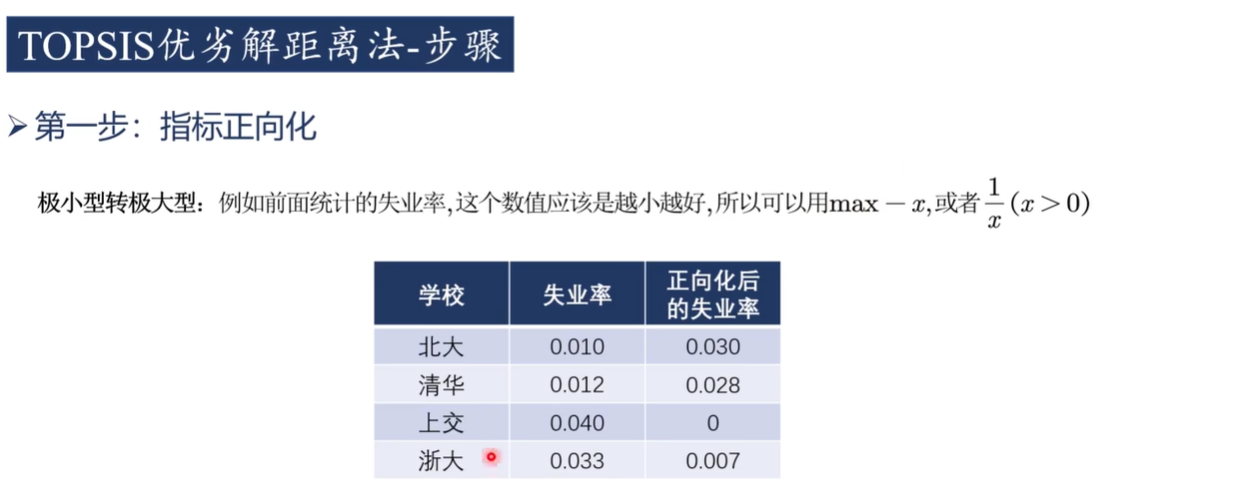
1)正向化
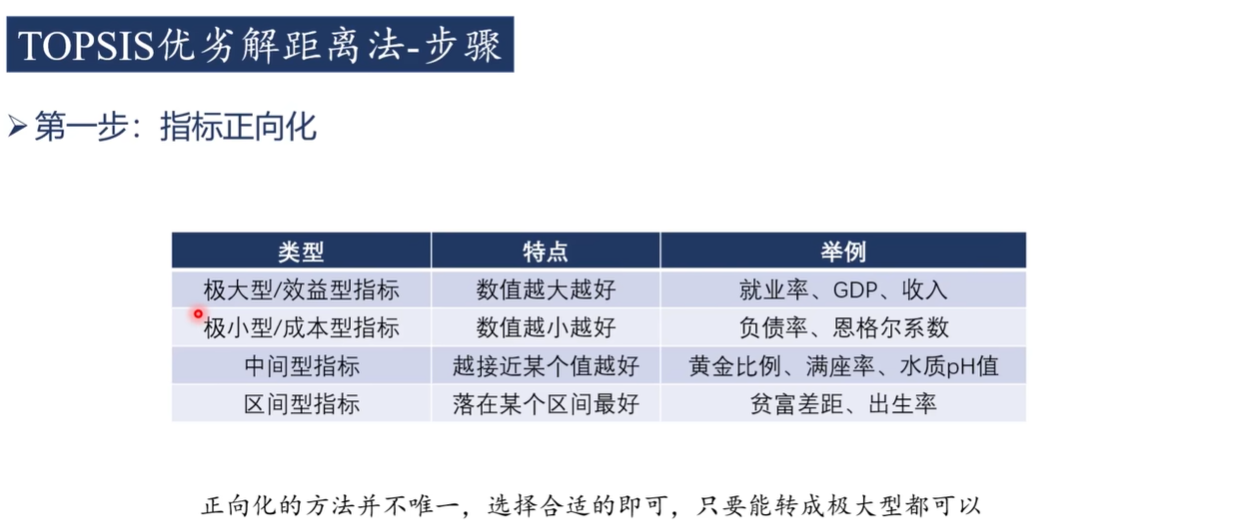
极小型转极大型
中间型转极大型

区间型转极大型

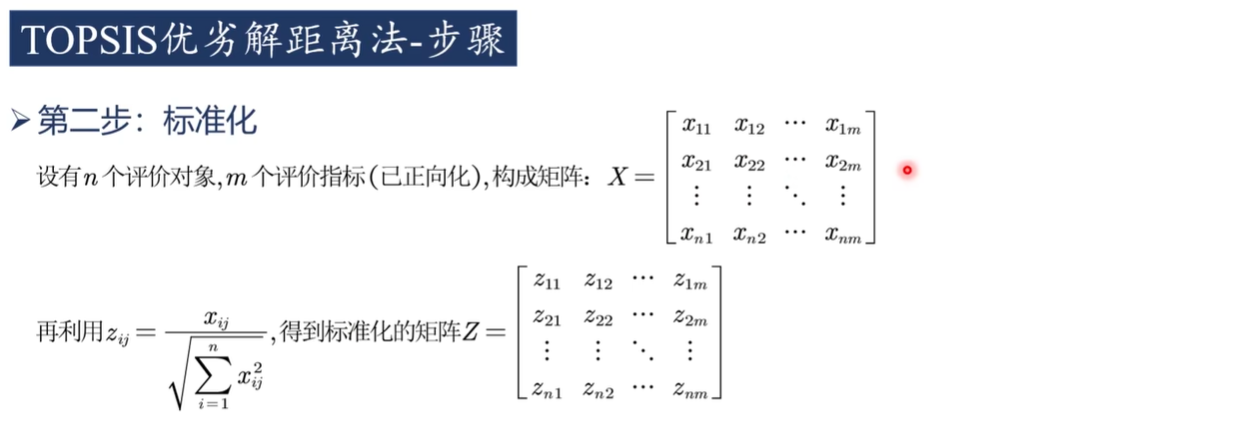
2)标准化
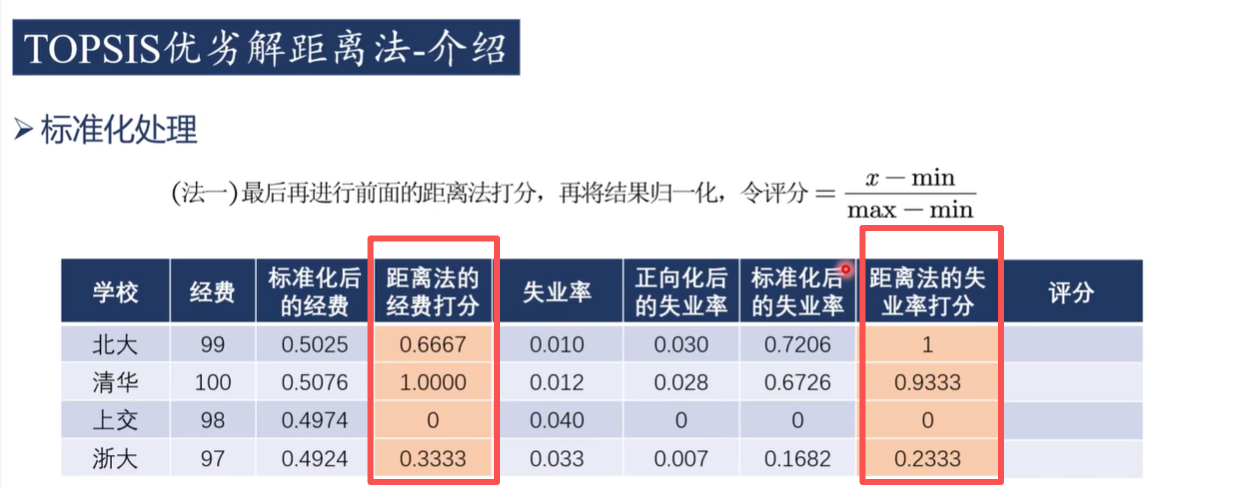
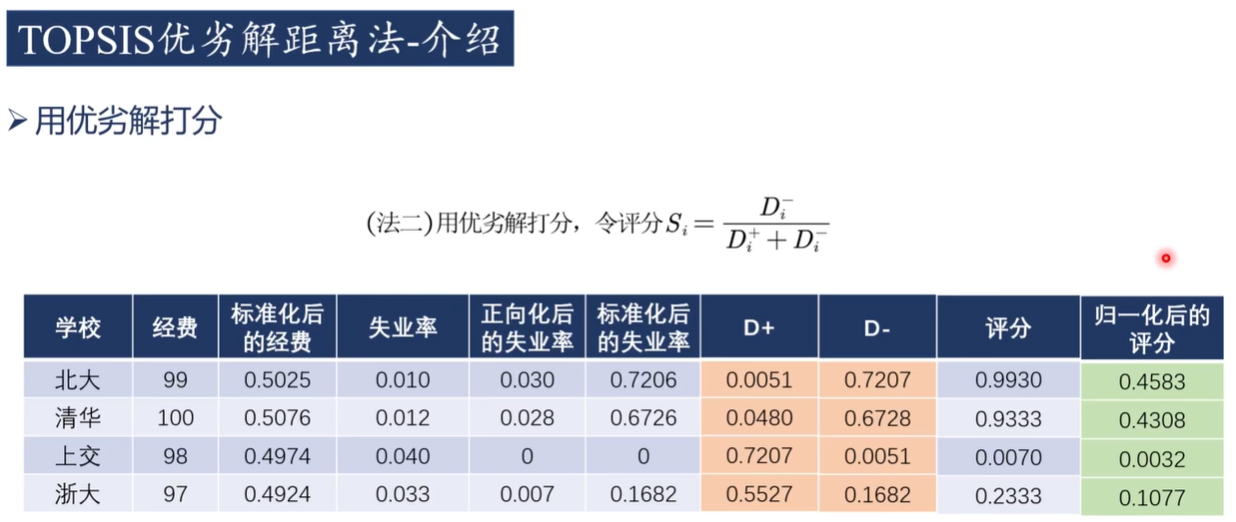
3)优劣解距离法打分



优秀论文



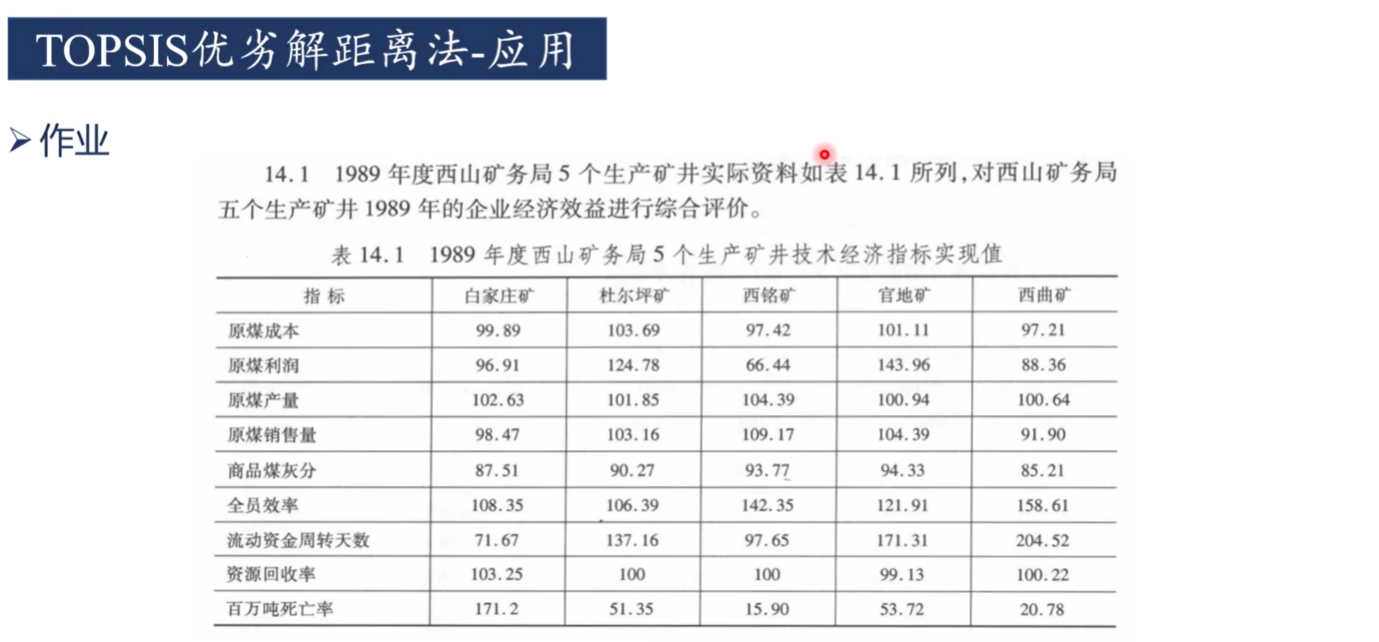
课后习题