前面描述 卷积,本文由卷积引入拉普拉斯变换。
拉普拉斯变换就是给傅里叶变换的 iωt 加了个实部,也可以反着理解,原函数乘以 e − β t e^{-\beta t} e−βt 再做傅里叶变换,本质上都是傅里叶变换的扩展。
加入实部的拉普拉斯变换在复平面展开,因此拉普拉斯变换除了有虚部的频率特性,还有实部的衰减特性。但不管怎么说,和傅里叶变换一样,它们均将时域分析转换为频域分析,这就是我经常采用的策略,横竖一颠倒,晴空万里。
看一个频域的运算特性,为什么时域的卷积运算可以转换为频域的乘法运算?看下图:
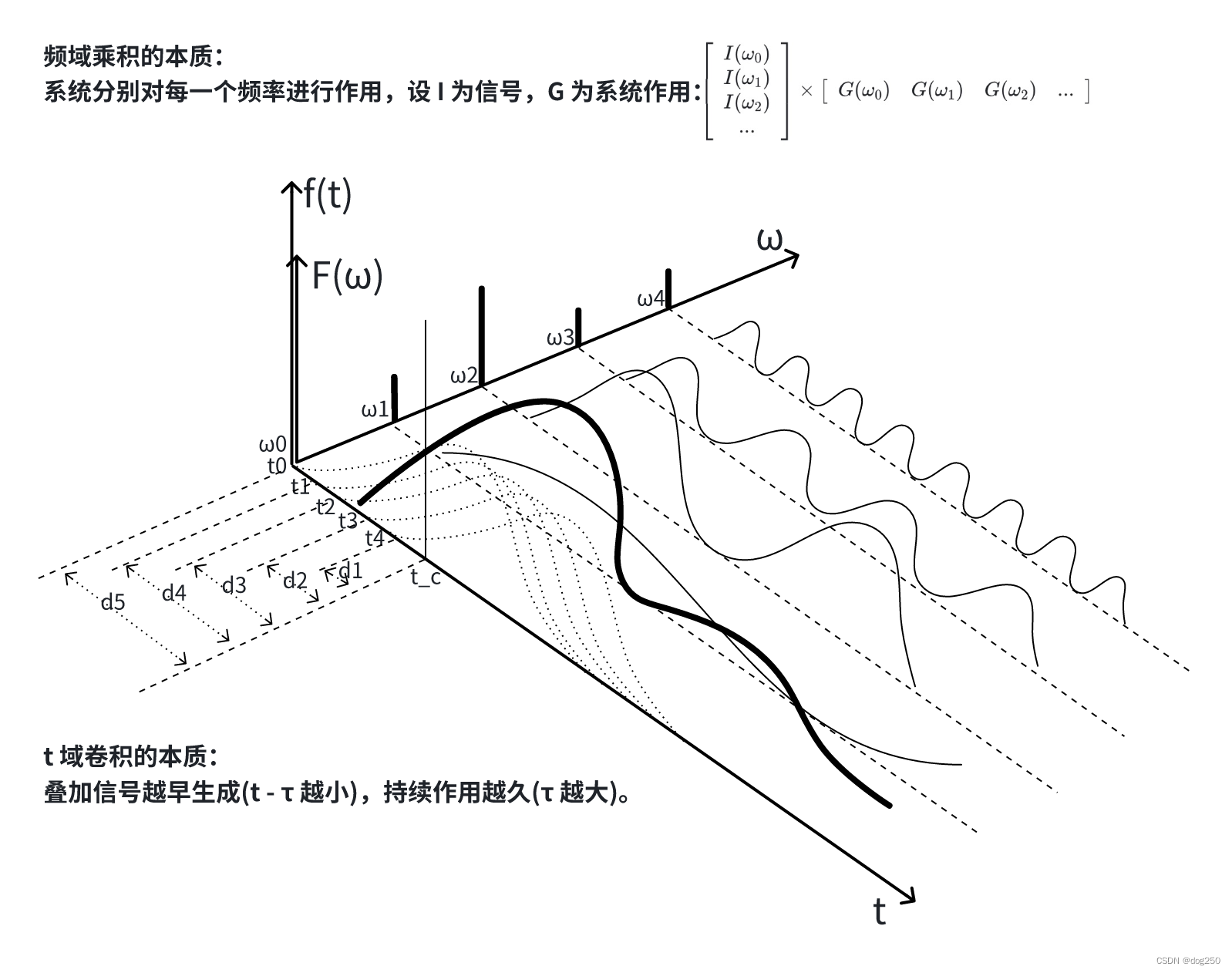
时域中,信号持续时间和信号生成时间是相对的,必须卷起来运算,而频域是个对称的空间维度,不同频率信号以及针对每个频率信号的处理全都 "摆在那里",因此可通过精巧阵法一下子算出来(如上图矩阵只是一个说明,本质上还是复数的乘法)。
展示一张实操图:

以 g/G 往 f/F 涂颜料为例,上图的卷积操作需要一边卷紧纸一边在 f 曲线上色,这也体现了时间域的特征,而下图的乘积操作则是一个空间域并行操作,颜料涂在 G 半边的曲线,对折一次就能将 F 半边染色。
再看拉普拉斯变换对运算的实际简化效果。
设 u 为输入,g 为系统作用函数,时域上 u * g 的卷积获得输出 x,由上面的时域,频域转换分析获知,拉普拉斯变换将卷积化为了乘法,即 F*G,再经拉普拉斯逆变换就能获得 x(t) 的以下形式:
- 若特征根没有虚部,要么是 x ( t ) = e a t ± e b t ± e c t . . . x(t)=e^{at}\pm e^{bt}\pm e^{ct}... x(t)=eat±ebt±ect...,要么收敛,要么发散,无震荡;
-
- 若有虚部,欧拉公式,要么是 x ( t ) = e a t ( sin ( b t ) . . . ) x(t)=e^{at}(\sin(bt)...) x(t)=eat(sin(bt)...),a > 0,震荡发散,a < 0,震荡收敛,a = 0,持续震荡。
发散的都不稳定,收敛的都稳定,区别在于是否震荡。
无需太过于关注极点的物理意义,拉普拉斯变换作为工具就只当它为工具,至于物理意义,一百个物理场景就能有一百个物理意义。
将极点看作逆变换后 x(t) 收敛,发散,震荡特征的总结是高尚的,而不是反过来。从 x(t) 的表达式可明确归纳出 a,b,c 等系数和函数收敛,发散,震荡的关系,而 a,b,c 等系数恰恰就是逆变换前 G(s) 分母为 0 的特征方程解的组成,将这些解在复平面的位置称作 "极点"。
因此根据 x(t) 的收敛,发散,震荡特性与极点实部虚部一一对应关系,通过分析 G(s) 的极点位置就能直接获得系统特性,无需再进行逆变换:
- 有极点实部 > 0,发散不稳定,因为 e 的正次方总趋向无穷大;
- 所有极点实部 < 0,收敛稳定,收敛速度取决于绝对值;
- 极点虚部 ≠ 0,系统震荡,因为 x(t) 包含一个 sin/cos。
这就是拉普拉斯变换 G(s) 作为工具的意义,称 G 为传递函数。
浙江温州皮鞋湿,下雨进水不会胖。