目录
3.4数组和特殊矩阵
3.4.2数组的存储结构
【二维数组按行优先存储的下标对应关系(2021)】
对于多维数组,有两种映射方法:按行优先和按列优先。
以二维数组为例,按行优先存储的基本思想是:先行后列,先存储行号较小的元素,行号相等先存储列号较小的元素。
设二维数组的行下标与列下标的范围分别为[0,h1]与[0,h2],则存储结构关系式为:
例如,对于数组 A[2][3],它按行优先方式在内存中的存储形式如图 3.18所示。

当以列优先方式存储时,得出存储结构关系式为:
例如,对于数组 A[2][3],它按列优先方式在内存中的存储形式如图 3.19所示。


3.4.3特殊矩阵的压缩存储
【对称矩阵压缩存储的下标对应关系(2018、2020)】
若对一个 n阶矩阵 A 中的任意一个元素 a ᵢ,ⱼ都有 a ᵢ,ⱼ = a ⱼ,ᵢ (1<=i,j<=n),则称其为对称矩阵。其中的元素可以划分为3个部分,即上三角区、主对角线和下三角区。

对于n阶对称矩阵,上三角区的所有元素和下三角区的对应元素相同,若仍采用二维数组存放,则会浪费几乎一半的空间,为此将n阶对称矩阵A存放在一维数组B[n(n+1)/2]中,即元素aᵢ,ⱼ,存放在bₖ以中。比如只存放下三角部分(含主对角)的元素。
在数组B中,位于元素aᵢ,ⱼ (i=>j)前面的元素个数为
第1行:1个元素(a₁,₁)。
第2行:2个元素(a₂,₁,a₂,₂)。
. . . . . .
第i-1行:i-1个元素(aᵢ-₁,₁, aᵢ-₁,₂,...,aᵢ-₁ ,ᵢ-₁ )。
第i行:j-1个元素(aᵢ,₁,aᵢ,₂,...,aᵢ,ⱼ-₁)。
因此,元素aᵢ,ⱼ 在数组B中的下标k=1+2+...+(i-1)+j-1=i(i-1)/2+j-1(数组下标从 0开始)。
因此,元素下标之间的对应关系如下:


注意:
二维数组 A[n] [n](行列都是n个元素)和 A[0..n-1] [0..n-1](行列都是n个元素)的写法是等价的。若数组写为 A[1..n][1..n],则说明指定了从下标 1开始存储元素。二维数组元素写为 a[i][j],注意数组元素下标i和j通常是从0开始的 。矩阵元素 通常写为 ai,j或 a(i)(j),注意行号i和列号j是从1开始的
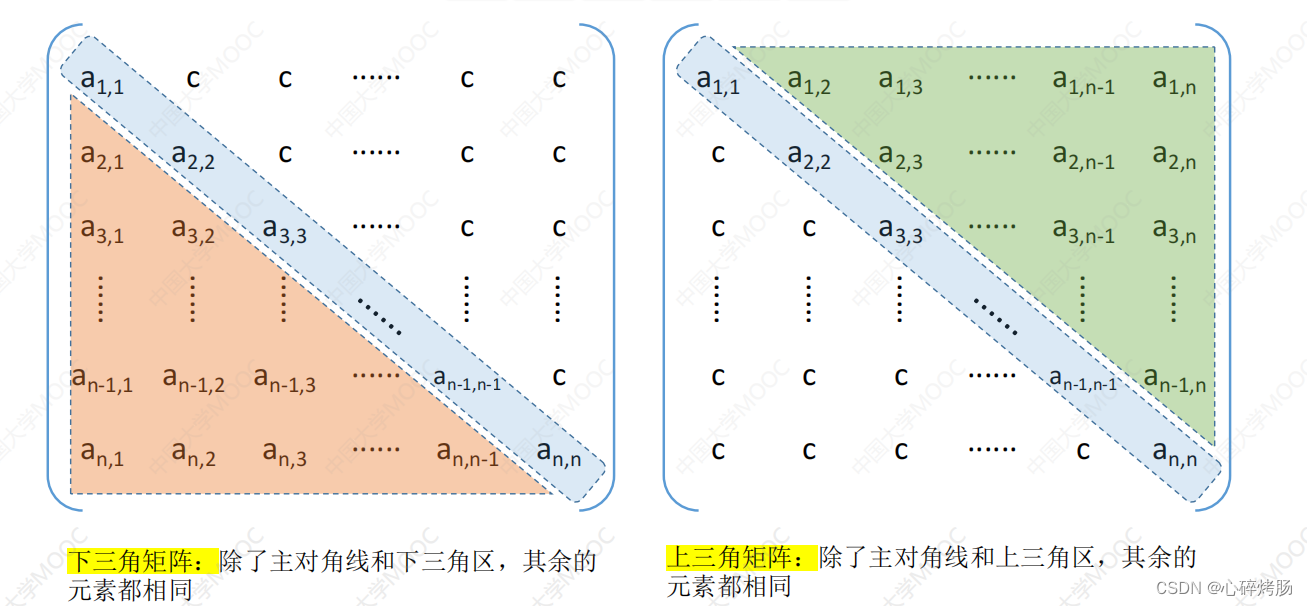
【上三角矩阵采用行优先存储的应用(2011)】
上三角矩阵[见图 3.22(b)]中,下三角区的所有元素均为同一常量。只需存储主对角线、上三角区上的元素和下三角区的常量一次,可将其压缩存储在B[n(n+1)/2+1]中。
在数组B中,位于元素aᵢ,ⱼ (i<=j)前面的元素个数为:
第1行:n个元素
第2行:n-1个元素
. . . . . .
第i-1行:n-i+2个元素
第i行:j-i个元素
因此,元素 aᵢ,ⱼ 在数组B中的下标
k=n+( n-1 )+...+( n-i+2 )+( j-i+1 )-1=( i-1 )( 2n-i +2 )/2+( j-i )
因此,元素下标之间的对应关系如下:

上三角矩阵在内存中的压缩存储形式如图所示。

以上推导均假设数组的下标从0开始,若题设有具体要求,则应该灵活应对。

【三对角矩阵压缩存储的下标对应关系(2016)】
由此可以计算矩阵A中3条对角线上的元素aᵢ,ⱼ(1≤i,j≤n,|i-j|≤1)在一维数组B中存放的下标为k=2i+j-3。
反之,若已知三对角矩阵中的某个元素aᵢ,ⱼ存放在一维数组B的第k个位置,则有i=[(k+ 1)/3+1],j=k-2i+3。
例如:
当k=0时,i=[(0+1)/3+1]=1,j=0-2x1+3=1,存放的是a₁,₁;
当k=2时,i=[(2+1)/3+1]=2,j=2-2x2+3=1,存放的是a₂,₁ ;
当k=4时,i=[(4+1)/3+1]=2,j=4-2x2+3=3,存放的是a₂,₃。
3.4.4稀疏矩阵
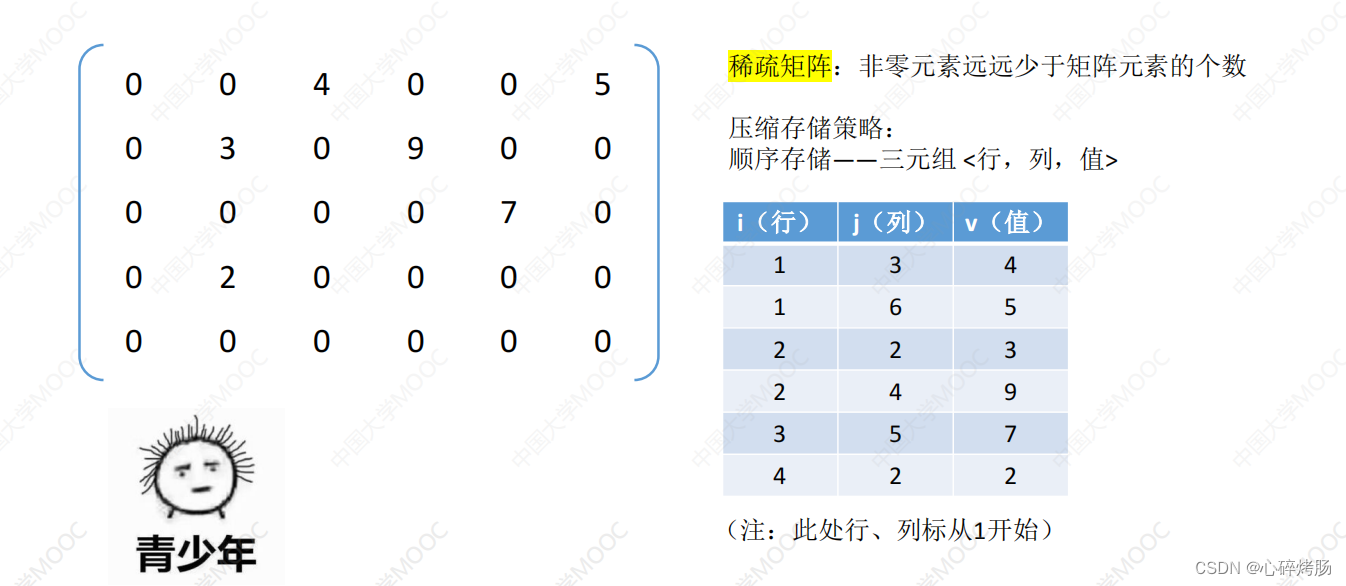
【存储稀疏矩阵需要保存的信息(2023)】
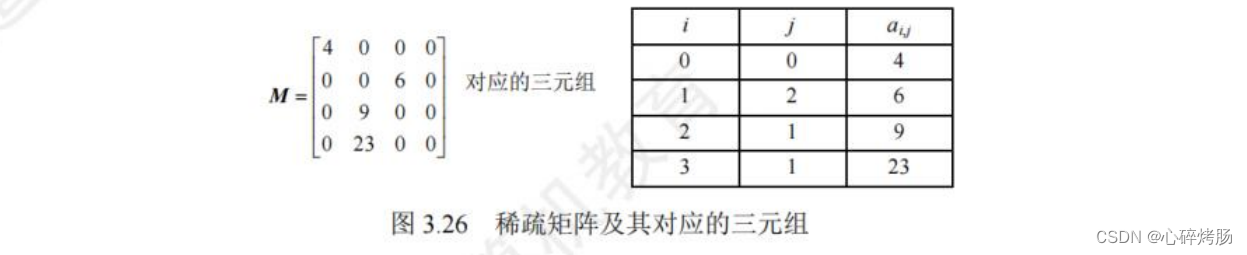
若采用常规的方法存储稀疏矩阵,则相当浪费存储空间,因此仅存储非零元素。但通常非零元素的分布没有规律,所以仅存储非零元素的值是不够的,还要存储它所在的行和列。因此,将非零元素及其相应的行和列构成一个三元组(行标i,列标j,值aᵢ,ⱼ ),如图 3.26 所示。然后按照某种规律存储这些三元组线性表。稀疏矩阵压缩存储后便失去了随机存取特性。
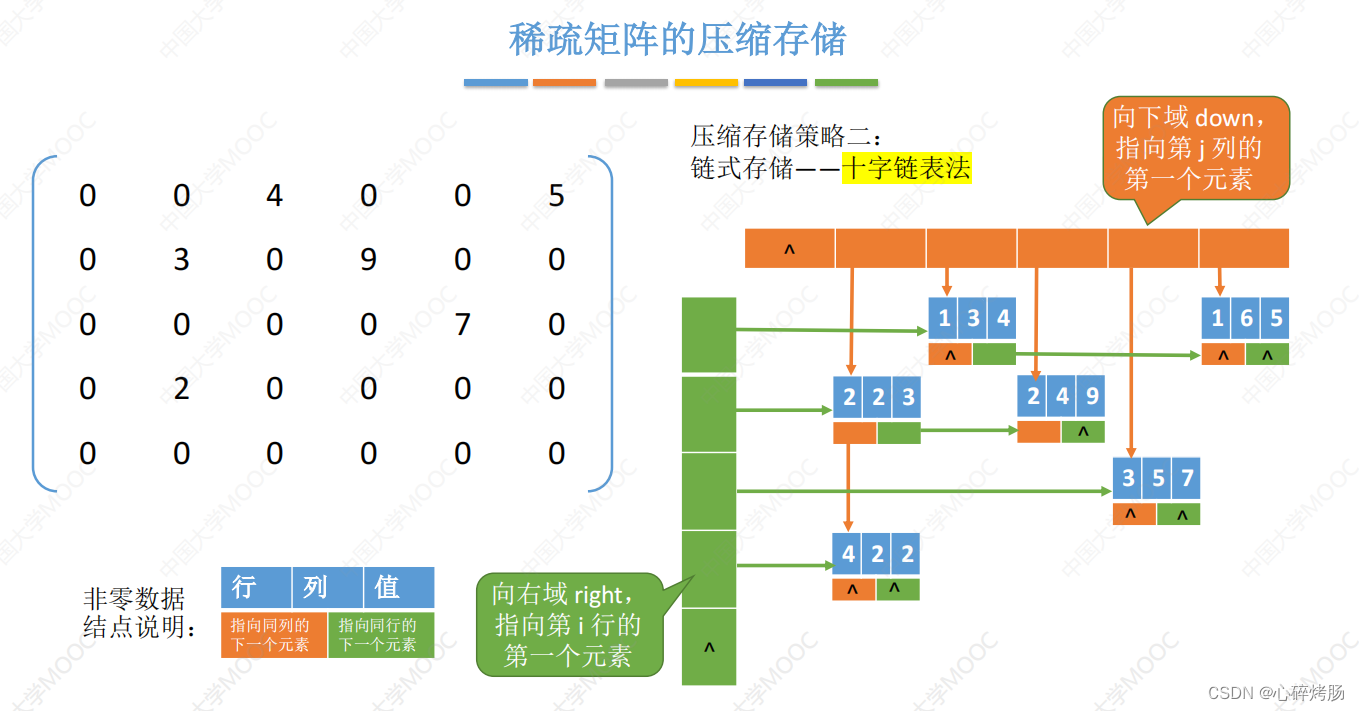
【适合稀疏矩阵压缩存储的存储结构(2017)】
稀疏矩阵的三元组表既可以采用数组存储,又可以采用十字链表存储(见6.2节后续讲解)。当存储稀疏矩阵时,不仅要保存三元组表,而且要保存稀疏矩阵的行数、列数和非零元素的个数。