by 木一
标签:#相机畸变 #畸变纠正 #鱼眼相机 #折射定律 #托勒密地图
引言
前文[1][2]我们介绍了针孔相机模型,以及针孔相机模型的相机标定过程,但针孔相机模型是对相机成像最简单的描述,实际的相机成像过程要远复杂很多。
首先相机成像原理虽然可以简化为小孔成像,但实际的相机并非针孔相机,按照小孔成像原理,小孔直径越小成像越清晰,事实上并非如此,因为光线还具有波动性,针孔越小,光的波动性就会越明显,衍射效应影响越大,导致成像变得模糊。另外小孔成像的亮度和成像范围也远远达不到相机成像要求。所以实际的相机采用的是凸透镜或镜头组来达到类似小孔成像的效果。
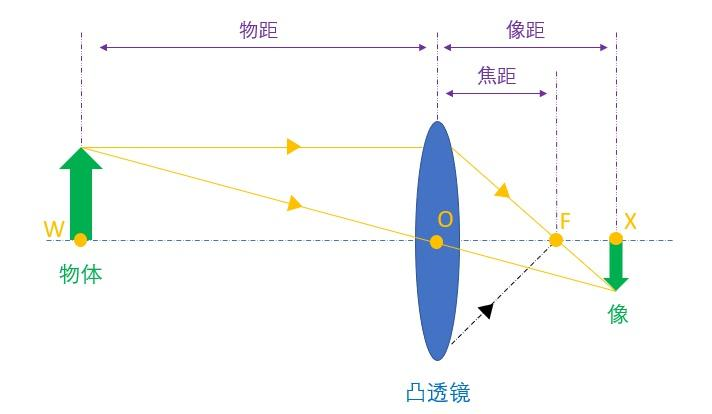
凸透镜成像 图源:https://zhuanlan.zhihu.com/p/469422543
相机畸变分类及成因
凸透镜出色的光线汇聚能力,能够将物体的像缩小到很小的范围,同时兼顾了成像的亮度和清晰度,这些特性使凸透镜非常适合作为相机镜头。而为了提高成像质量,相机镜头通常采用凹凸透镜组合实现成像。
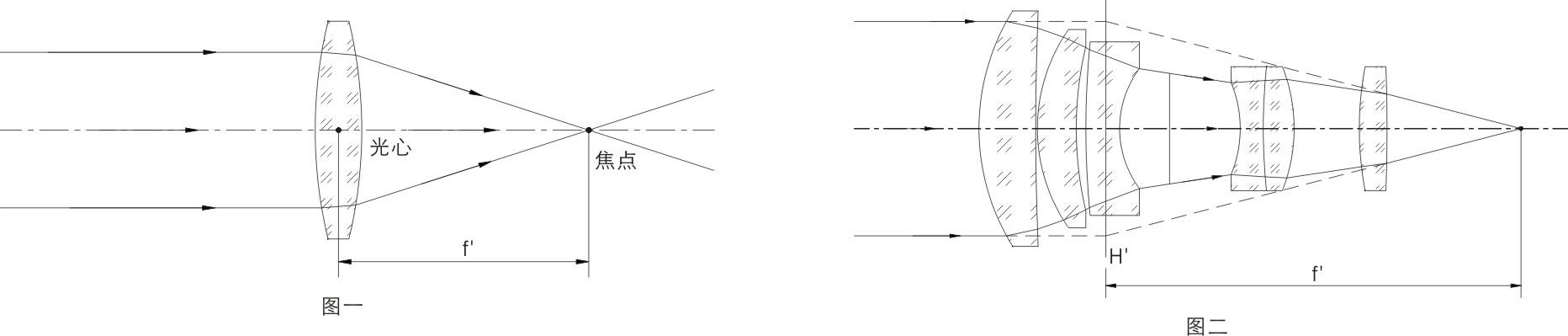
透镜组合 图源:广东奥普特科技股份有限公司,奥普特,OPT,奥普特官网,广东奥普特科技
用凸透镜(透镜组)做镜头,尽管形式改了,但是成像投影的方式并没有变化,同样可以用针孔相机模型来进行描述。在针孔成像过程中,像与物保持着很多不变的性质,比如直线经过变换仍然是直线,圆锥曲线(比如椭圆)经过变换仍然是圆锥曲线,正因为这些不变的几何性质,使得照片与原场景存在着某种相似性,所以我们看照片才具备真实感。
而在实际应用中,相机的凸透镜成像会偏离相似性,也就是我们所说的产生了畸变,畸变一般是由于相机镜头的制造工艺、安装误差等原因造成的。通常相机畸变可以分类两类:径向畸变和切向畸变。
径向畸变
径向畸变是指是由镜头透镜物理性质或镜片组结构引起的成像画面向外膨胀或向内收缩的现象,简单来说就是直线经过成像后变成了曲线,这并不会影响像的清晰度,而只影响像与物的相似性,径向畸变分为桶形畸变和枕形畸变:

径向畸变1 图源:关于镜头畸变问题的总结_镜头畸变计算公式-CSDN博客
形成这种现象的主要原因是透镜在不同位置的放大倍率不同。如下图所示,将靠近镜头中心部分所成的像记作y1,远离镜头中心部分所成的像记作y2,当y1/h1 > y2/h2时,所成的像是从中心往外放大的,也就是桶形畸变。反之则是枕形畸变。
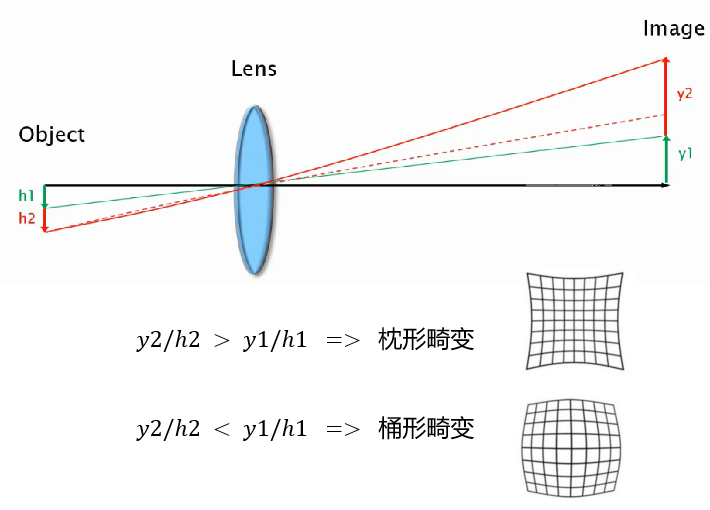
径向畸变2 图源:https://blog.csdn.net/qq_35247586/article/details/130047063
通常情况下,广角镜头容易产生桶形畸变,长焦镜头容易产生枕形畸变。
切向畸变
切向畸变是由于透镜本身与相机传感器平面(成像平面)或图像平面不平行而产生的,这种情况多是由于透镜被粘贴到镜头模组上的安装偏差导致。通常情况下只考虑径向畸变即可。
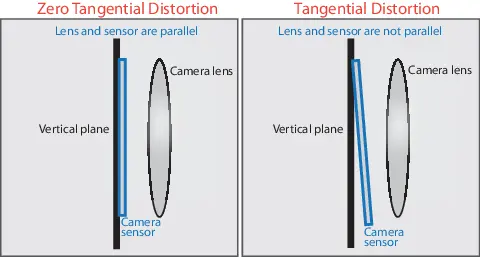
切向畸变 图源:镜头畸变的那些事 | 清新的日子
畸变纠正
相机镜头由于要兼顾不同应用场景,畸变不可避免,因此需要对产生了畸变的图像进行畸变纠正。前文我们介绍的针孔相机模型和相机标定方法是基于无畸变的成像过程的,所标定的相机内参也是假定相片不存在畸变。因此畸变纠正需要在相机标定之前完成。基于特定的畸变模型,求解畸变系数,对相片进行畸变纠正,产生无畸变相片,再基于无畸变相片进行相机标定。

畸变纠正 图源:透镜畸变及校正模型_径向畸变-CSDN博客
常用于描述相机畸变的有多项式模型和除法模型,目前比较常用的机器视觉库中基本上也都集成了畸变纠正算法,比如OpenCV中集成张正友标定法,且只考虑了畸变模型中影响较大的径向畸变,具体算法介绍也比较普遍了,不再赘述。具体可参考:https://www.cnblogs.com/Jack-Elvis/p/16078743.html
拓展:鱼眼相机
大多时候,我们并不希望镜头有畸变,但在一些特殊应用场景中,也需要牺牲物像的相似性,以获取其他方面的优势,比如为了获取更大的视角范围所设计的超广角相机、鱼眼相机等。
上文我们介绍了焦距和视角的关系,容易得知,焦距越短视角越大,但实际情况是普通超广角相机即便拥有很短的焦距,也很难覆盖180°的视角范围,因此人们又发明了鱼眼镜头。鱼眼镜头的灵感顾名思义是来自水下的鱼。如下图所示,由于水的折射率比空气大,从水下向上看时,水面上的空间会被压缩到一个半球形空间,而球形外部,则是是来自水面下景色的反射。这样所有水面上的景色便被压缩在一个圈内,这个圈也被叫做斯涅耳窗口 。关于鱼眼镜头的介绍,这边文章中介绍的很全面,本文不再过多阐述:https://zhuanlan.zhihu.com/p/29273352。
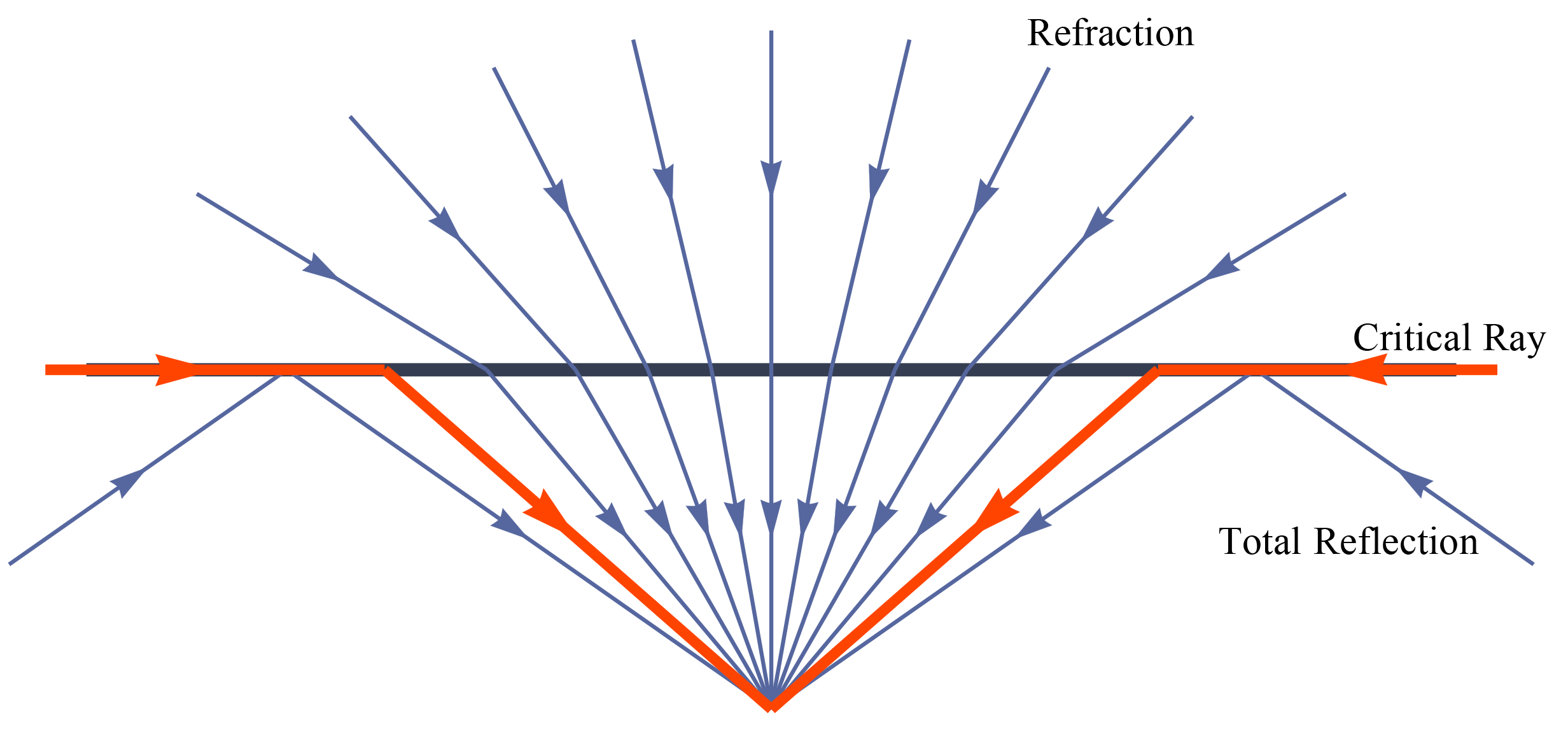
空气-水界面处的光线折射与全反射 图源:https://zhuanlan.zhihu.com/p/29273352

斯涅耳窗口现象 图源:https://zhuanlan.zhihu.com/p/29273352

鱼眼相机 图源:百度百科
拓展:折射定律
前面提到一个有趣的现象:斯涅耳窗口 ,关于这个现象在查阅资料时又关联到另外一个知识点:斯涅尔定律 ,出于好奇检索了一下,发现这便是从小便学过的折射定律,并且折射定律的发现历程,也是经历了很多曲折:
最早的研究起源于公元二世纪,古希腊科学家托勒密做了一个关于光的折射实验。他在一个圆盘上装两把能绕盘心旋转的尺子,将圆盘的一半浸入水中。让光线由空气射入水中,就得到它在水中的折射光线,转动两把尺子,使它们分别与入射光线和折射光线重合。然后取出圆盘,按尺子的位置刻下人射角和折射角。尽管托勒密的实验方法是正确的,实验结果相当精确,与现代值几乎没有多大的差别。但是,由于他测量得不够精确,得出了一个错误的结论,他认为折射角与入射角成正比。托勒密因此错过了一次发现折射定律的机会。
之后伊朗学者伊本·沙尔在984年的专著《论点火镜子与透镜》里最先正确地描述折射定律。可惜的是其它学者并没有注意到他的研究结果。之后很多年,人们都是从托勒密的错误理论开始研究折射。
伊本·沙尔的手稿 图源:维基百科
之后,阿拉伯的科学家阿勒·哈增重复了托勒密的测量,证明入射角和折射角之比是常数的说法是错误的。
17世纪初,开普勒对光的折射现象进行了深入的研究,虽然没有找到正确的折射定律表达式,但通过这些实验发现了全反射,并把他的发现写进了《折射光学》一书。
正确的折射定律是两个人建立的------荷兰数学家威里布里德•斯涅耳 和法国数学家笛卡儿。
1621年,在开普勒的研究结果的启示下,斯涅耳做了进一步的实验,并发现了入射角与折射角的余割之比为一常数的规律。斯涅耳的这一折射定律是从实验中得到的,没有做任何的理论推导,虽然正确,但却从未正式公布过。
1637年,法国数学家笛卡儿进一步完善了斯涅耳光的折射定律,第一次给出了折射定律的现代表述形式,并在《屈光学》一书中论述了这个问题。
最后还有一个法国数学家费马,由于笛卡尔是从光的微粒观念中推导出折射定律的,这引起了费马的怀疑,费马没有根据光折射的实验现象对光作任何假设,只是利用光是以有限速度传播的这一十七世纪最伟大的发现,用数学方法给出了折射定律的证明。
再发散一下,把大家带跑偏的托勒密,也是将地心说理论体系构建完善的那个人,托勒密通过整理之前六百年的天文学文献,加上自己长期观测的结果,建立了完整的地心体系理论,基本上圆满地解释了当时人们所能观察到的所有天文学现象。甚至在他死后的整整15个世纪中,天文学的教科书都在教授他的理论。

托勒密体系的宇宙图 图源:维基百科
此外,托勒密所著《地理学指南》对地图学的发展做出了巨大的贡献,影响贯穿至今。他综合前人的研究成果,提出在地图上绘制经纬线网的概念,为此,托勒密测量了地中海一带重要城市和据点的经纬度,还提出了投影问题,给出了圆锥投影和球面投影两种方法。《地理学指南》第8卷由几十幅地图组成。他用普通圆锥投影,也就是把经纬线绘成简单的扇形,绘制了世界地图,即著名的"托勒密地图"。
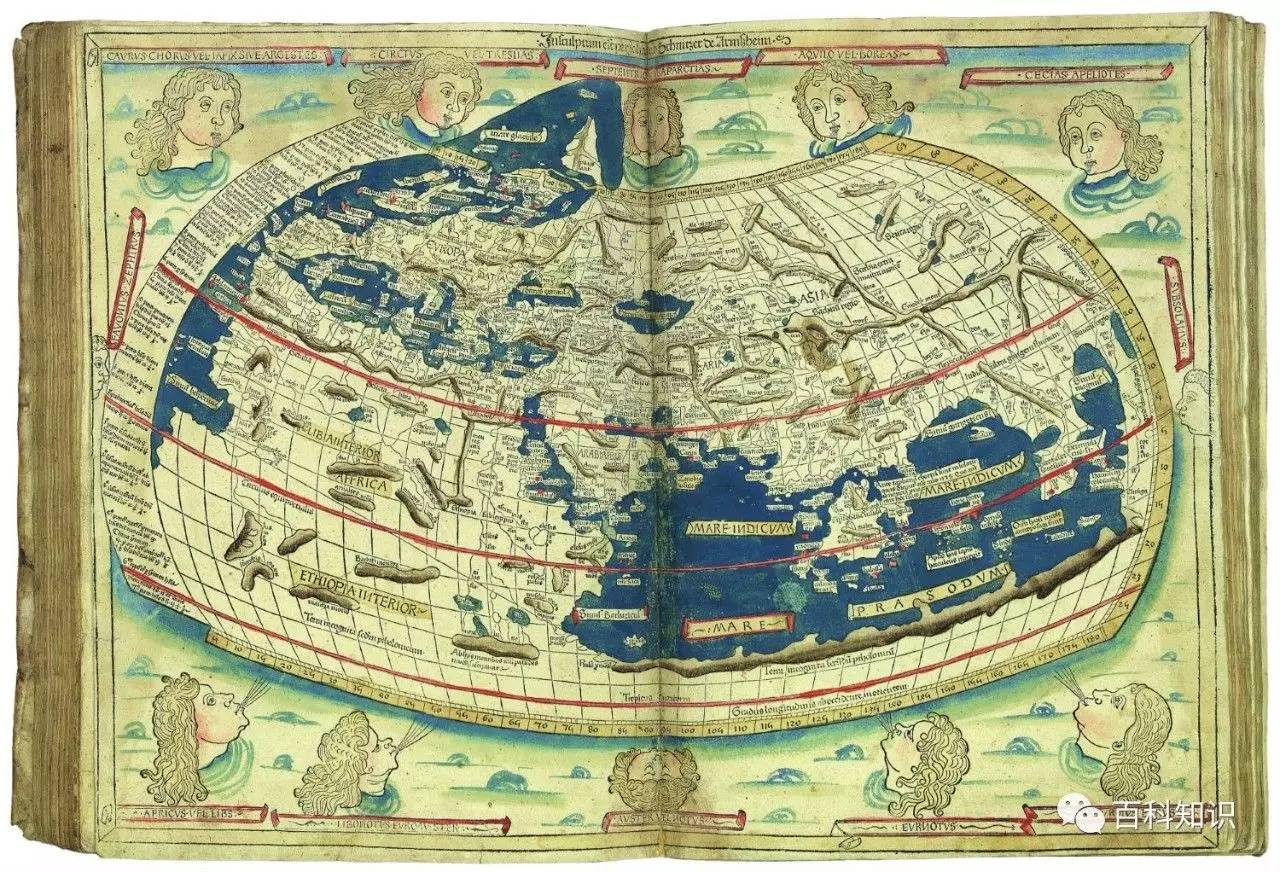
托勒密世界地图图源:影响世界制图史的九张地图
怎么就聊到了地图呢?因为小编是一名GISer,也就是专业为"地图学与地理信息系统",地图投影几乎是地图学第一节课便要学习的内容。所以这位托勒密也算祖师爷级别的人物了。并且前面提到的鱼眼相机,在成像过程也存在一个投影模型,当然此投影非彼投影,但总觉得,万事万物皆有联系,好了,再说就唯心了,有兴趣的同学可以挖掘看看。
这些故事现在看起来似乎觉得有趣,但是回过头来想想,如今我们以为的常识,其实是先驱们对真理不懈的探索追求才得到的。摘抄一句博客中的话"虽然托勒密的错误延续了一千三百余年,而这也是他的价值所在。科学发现的轨迹就是在错误和正确之间来回震荡的一条曲线;人们总是会犯错误,而这些错误,不过是正确的前奏罢了。"
参考:
https://zhuanlan.zhihu.com/p/29273352
https://zhuanlan.zhihu.com/p/469422543
https://www.cnblogs.com/Jack-Elvis/p/16078743.html
广东奥普特科技股份有限公司,奥普特,OPT,奥普特官网,广东奥普特科技
https://zh.wikipedia.org/wiki/斯涅尔定律
折射定律的发现及证明过程 开源地理空间基金会中文分会 开放地理空间实验室
科学网---托勒密为什么没有归纳出折射定律? - 王国强的博文
https://www.youtube.com/watch?v=i__IGU1Zm64
荣耀舰队托勒密_上.html
科学网---从裴秀和托勒密,话地图学的发展 - 高关中的博文
关注Mapmost,持续更新GIS、三维美术、计算机技术干货
Mapmost是一套以三维地图和时空计算为特色的数字孪生底座平台,包含了空间数据管理工具(Studio)、应用开发工具(SDK)、应用创作工具(Alpha)。平台能力已覆盖城市时空数据的集成、多源数据资源的发布管理,以及数字孪生应用开发工具链,满足企业开发者用户快速搭建数字孪生场景的切实需求,助力实现行业领先。