前言
最近看这两个滤波器设计嘛,就试着来写一下
主要从双线性变换,z变换,然后举一个例子来进行一下滤波器的设计。
例子
我们考虑传递函数如下的low pass filter
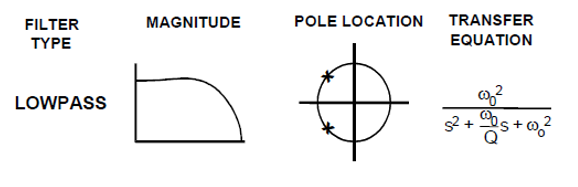
IIR滤波器
脉冲响应不变法
考虑这个传递函数 H ( s ) = w 0 2 s 2 + w 0 Q s + w 0 2 H(s)=\frac{w_0^2}{s^2+\frac{w_0}{Q}s+w_0^2} H(s)=s2+Qw0s+w02w02
为了更好地将H(s)拆分开来,我们考虑分母的因式分解
假设 H ( s ) H(s) H(s)存在两个根,解一元二次方程,有:
p 1 , 2 = − w 0 2 Q ± 1 − 1 4 Q 2 p_{1,2}=-\frac{w_0}{2Q} \pm \sqrt{1-\frac{1}{4Q^2}} p1,2=−2Qw0±1−4Q21
为了方便计算,我们记
α = − w 0 2 Q \alpha =-\frac{w_0}{2Q} α=−2Qw0
β = w 0 1 − 1 4 Q 2 \beta = w_0\sqrt{1-\frac{1}{4Q^2}} β=w01−4Q21
因此我们知道
p 1 = α + j β p_1=\alpha + j\beta p1=α+jβ
p 2 = α − j β p_2=\alpha-j\beta p2=α−jβ
那我们的H(s)此时变成了:
H ( s ) = w 0 2 ( s − p 1 ) ( s − p 2 ) H(s)=\frac{w_0^2}{(s-p_1)(s-p_2)} H(s)=(s−p1)(s−p2)w02
我们假设这个式子可以展开,那么我们可以得到H(s)如下:
H ( s ) = A s − p 1 + B s − p 2 H(s)=\frac{A}{s-p1} + \frac{B}{s-p_2} H(s)=s−p1A+s−p2B
这里A和B是待定的,我们有
w 0 2 ( s − p 1 ) ( s − p 2 ) = A s − p 1 + B s − p 2 \frac{w_0^2}{(s-p_1)(s-p_2)}=\frac{A}{s-p_1}+\frac{B}{s-p_2} (s−p1)(s−p2)w02=s−p1A+s−p2B
这里我们其实可以计算出来,两边同时乘以分母,就有
A ( s − p 2 ) + B ( s − p 1 ) = w 0 2 A(s-p_2)+B(s-p_1)=w_0^2 A(s−p2)+B(s−p1)=w02
求得A和B如下:
A = w 0 2 p 1 − p 2 B = w 0 2 p 2 − p 1 A = \frac{w_0^2}{p_1-p_2} \\ B=\frac{w_0^2}{p_2-p_1} A=p1−p2w02B=p2−p1w02
然后我们将H(s)转换到时域上考量,使用你拉布拉斯变换
L − 1 { A s − p 1 } = A e p 1 t L − 1 { A s − p 2 } = B e p 2 t \mathcal{L}^{-1}\{ \frac{A}{s-p_1}\}=Ae^{p_1t}\\\mathcal{L}^{-1}\{ \frac{A}{s-p_2}\}=Be^{p_2t} L−1{s−p1A}=Aep1tL−1{s−p2A}=Bep2t
综上,得到
h ( t ) = A e p 1 t + B e p 2 t h(t)=Ae^{p_1t}+Be^{p_2t} h(t)=Aep1t+Bep2t
带入
p 1 = α + j β p 2 = α − j β p_1=\alpha+\mathcal{j}\beta\\p_2=\alpha-\mathcal{j}\beta p1=α+jβp2=α−jβ
有 h ( t ) = e α t ( A 1 e j β t + A 2 e − j β t ) h(t)=e^{\alpha t}(A_1e^{\mathcal{j}\beta t}+A_2e^{-\mathcal{j}\beta t}) h(t)=eαt(A1ejβt+A2e−jβt)
其实到这里就已经可以算作阶数了,但是这个可以继续化简减少工作量,我们利用欧拉公式
e j β t = cos ( β t ) + j sin ( β t ) e − j β t = cos ( β t ) − j sin ( β t ) e^{\mathcal{j}\beta t}=\cos(\beta t) + \mathcal{j}\sin(\beta t) \\ e^{\mathcal{-j}\beta t}=\cos(\beta t) - \mathcal{j}\sin(\beta t) ejβt=cos(βt)+jsin(βt)e−jβt=cos(βt)−jsin(βt)
假定我们在实数域上讨论和考虑,那么最终化简得到
h ( t ) = 2 A e α t c o s ( β t ) h(t)=2Ae^{\alpha t}cos(\beta t) h(t)=2Aeαtcos(βt)
这里是直接计算得到脉冲响应函数。
双线性变换法
还是考虑这个s域上的传递函数
H ( s ) = ω 0 2 s 2 + ω 0 Q s + ω 0 2 H(s) = \frac{\omega_0^2}{s^2 + \frac{\omega_0}{Q}s + \omega_0^2} H(s)=s2+Qω0s+ω02ω02
使用双线性变换法呢,则是直接将H(s)进行z变换,得我们令
s = 2 T 1 − z − 1 1 + z − 1 s=\frac{2}{T} \frac{1-z^{-1}}{1+z^{-1}} s=T21+z−11−z−1
求解极点,求解特征方程的根,即传递函数分母的零点:
s 2 + ω 0 Q s + ω 0 2 = 0 s^2 + \frac{\omega_0}{Q}s + \omega_0^2 = 0 s2+Qω0s+ω02=0
根为:
p 1 , 2 = − ω 0 2 Q ± j ω 0 1 − 1 4 Q 2 p_{1,2} = -\frac{\omega_0}{2Q} \pm j \omega_0 \sqrt{1 - \frac{1}{4Q^2}} p1,2=−2Qω0±jω01−4Q21
设:
α = − ω 0 2 Q \alpha = -\frac{\omega_0}{2Q} α=−2Qω0
β = ω 0 1 − 1 4 Q 2 \beta = \omega_0 \sqrt{1 - \frac{1}{4Q^2}} β=ω01−4Q21
将 s s s 替换为双线性变换的表达式:
s = 2 T 1 − z − 1 1 + z − 1 s = \frac{2}{T} \frac{1 - z^{-1}}{1 + z^{-1}} s=T21+z−11−z−1
代入 H ( s ) H(s) H(s) 中:
H ( 2 T 1 − z − 1 1 + z − 1 ) = ω 0 2 ( 2 T 1 − z − 1 1 + z − 1 ) 2 + ω 0 Q ( 2 T 1 − z − 1 1 + z − 1 ) + ω 0 2 H\left( \frac{2}{T} \frac{1 - z^{-1}}{1 + z^{-1}} \right) = \frac{\omega_0^2}{\left( \frac{2}{T} \frac{1 - z^{-1}}{1 + z^{-1}} \right)^2 + \frac{\omega_0}{Q} \left( \frac{2}{T} \frac{1 - z^{-1}}{1 + z^{-1}} \right) + \omega_0^2} H(T21+z−11−z−1)=(T21+z−11−z−1)2+Qω0(T21+z−11−z−1)+ω02ω02
将分子分母进行通分并展开,可以得到:
H ( z ) = ω 0 2 ( 1 + z − 1 ) 2 ( 2 T ) 2 ( 1 − z − 1 ) 2 + 2 ω 0 Q T ( 1 − z − 1 ) ( 1 + z − 1 ) + ω 0 2 ( 1 + z − 1 ) 2 H(z) = \frac{\omega_0^2 \left( 1 + z^{-1} \right)^2}{\left( \frac{2}{T} \right)^2 \left( 1 - z^{-1} \right)^2 + \frac{2 \omega_0}{QT} \left( 1 - z^{-1} \right) \left( 1 + z^{-1} \right) + \omega_0^2 \left( 1 + z^{-1} \right)^2} H(z)=(T2)2(1−z−1)2+QT2ω0(1−z−1)(1+z−1)+ω02(1+z−1)2ω02(1+z−1)2
最终得到的离散时间传递函数 H ( z ) H(z) H(z) 形式为:
H ( z ) = b 0 + b 1 z − 1 + b 2 z − 2 1 + a 1 z − 1 + a 2 z − 2 H(z) = \frac{b_0 + b_1 z^{-1} + b_2 z^{-2}}{1 + a_1 z^{-1} + a_2 z^{-2}} H(z)=1+a1z−1+a2z−2b0+b1z−1+b2z−2
上下一比对,我们最终可以推导出 b 0 , b 1 , b 2 , a 1 , a 2 b_0,b_1,b_2,a_1,a_2 b0,b1,b2,a1,a2的参数计算公式
b 0 = ω 0 2 T 2 4 + 2 ω 0 T Q + ω 0 2 T 2 b_0 = \frac{\omega_0^2 T^2}{4 + \frac{2\omega_0 T}{Q} + \omega_0^2 T^2} b0=4+Q2ω0T+ω02T2ω02T2
b 1 = 2 b 0 b_1 = 2b_0 b1=2b0
b 2 = b 0 b_2 = b_0 b2=b0
a 1 = 2 ( ω 0 2 T 2 − 4 ) 4 + 2 ω 0 T Q + ω 0 2 T 2 a_1 = \frac{2(\omega_0^2 T^2 - 4)}{4 + \frac{2\omega_0 T}{Q} + \omega_0^2 T^2} a1=4+Q2ω0T+ω02T22(ω02T2−4)
a 2 = 4 − 2 ω 0 T Q + ω 0 2 T 2 4 + 2 ω 0 T Q + ω 0 2 T 2 a_2 = \frac{4 - \frac{2\omega_0 T}{Q} + \omega_0^2 T^2}{4 + \frac{2\omega_0 T}{Q} + \omega_0^2 T^2} a2=4+Q2ω0T+ω02T24−Q2ω0T+ω02T2
FIR滤波器
窗函数法
还是考虑这个传递函数
H ( s ) = ω 0 2 s 2 + ω 0 Q s + ω 0 2 H(s) = \frac{\omega_0^2}{s^2 + \frac{\omega_0}{Q}s + \omega_0^2} H(s)=s2+Qω0s+ω02ω02
为了找到其时域冲激响应 h ( t ) h(t) h(t),我们需要对 H ( s ) H(s) H(s) 进行拉普拉斯逆变换。首先,重写传递函数:
H ( s ) = w 0 2 ( s + α 1 ) ( s + α 2 ) H(s) = \frac{w_0^2}{(s + \alpha_1)(s + \alpha_2)} H(s)=(s+α1)(s+α2)w02
其中, α 1 \alpha_1 α1 和 α 2 \alpha_2 α2 是特征根,可以通过解方程 s 2 + w 0 Q s + w 0 2 = 0 s^2 + \frac{w_0}{Q}s + w_0^2 = 0 s2+Qw0s+w02=0 得到:
α 1 , α 2 = − w 0 2 Q ± w 0 ( 1 4 Q 2 − 1 ) \alpha_1, \alpha_2 = \frac{-w_0}{2Q} \pm w_0 \sqrt{\left(\frac{1}{4Q^2} - 1\right)} α1,α2=2Q−w0±w0(4Q21−1)
然后,采用部分分式分解:
H ( s ) = A s + α 1 + B s + α 2 H(s) = \frac{A}{s + \alpha_1} + \frac{B}{s + \alpha_2} H(s)=s+α1A+s+α2B
我们可以通过匹配系数法找到 A A A 和 B B B。
对于每个分式:
L − 1 { A s + α 1 } = A e − α 1 t \mathcal{L}^{-1}\left\{\frac{A}{s + \alpha_1}\right\} = A e^{-\alpha_1 t} L−1{s+α1A}=Ae−α1t
L − 1 { B s + α 2 } = B e − α 2 t \mathcal{L}^{-1}\left\{\frac{B}{s + \alpha_2}\right\} = B e^{-\alpha_2 t} L−1{s+α2B}=Be−α2t
因此,时域冲激响应 h ( t ) h(t) h(t) 为:
h ( t ) = A e − α 1 t + B e − α 2 t h(t) = A e^{-\alpha_1 t} + B e^{-\alpha_2 t} h(t)=Ae−α1t+Be−α2t
假设采样率为 f s f_s fs,我们将时域冲激响应 h ( t ) h(t) h(t) 离散化得到 h d [ n ] h_d[n] hd[n]:
h d [ n ] = h ( n T ) = A e − α 1 n T + B e − α 2 n T h_d[n] = h(nT) = A e^{-\alpha_1 nT} + B e^{-\alpha_2 nT} hd[n]=h(nT)=Ae−α1nT+Be−α2nT
其中 T = 1 f s T = \frac{1}{f_s} T=fs1。
选择一个适当的窗函数(如Hamming窗、Hann窗等) w [ n ] w[n] w[n],并将其应用到采样后的冲激响应上,以得到最终的FIR滤波器系数。
假设我们使用Hamming窗 w [ n ] w[n] w[n]:
h w [ n ] = h d [ n ] ⋅ w [ n ] h_w[n] = h_d[n] \cdot w[n] hw[n]=hd[n]⋅w[n]
其中,Hamming窗的定义为:
w [ n ] = 0.54 − 0.46 cos ( 2 π n N − 1 ) w[n] = 0.54 - 0.46 \cos\left(\frac{2 \pi n}{N-1}\right) w[n]=0.54−0.46cos(N−12πn)
最终的FIR滤波器系数为:
h [ n ] = h w [ n ] h[n] = h_w[n] h[n]=hw[n]