第15届蓝桥杯Python青少组选拔赛(STEMA)2023年8月真题
题目总数: 11 总分数: 400
一、单选题
第 1 题 单选题
以下不符合 Python 语言变量命名规则的是( )。
A. k
B. 2_k
C. _k
D. ok
答案 B
第 2 题 单选题
已知: s = python ,执行 print( s[-1] ) 语句后,输出的结果是( )。
A. python
B. p
C. nohtyp
D. n
答案 D
第 3 题 单选题
运行 print(type(str(3.14))) 语句后,输出的是( )。
A. class 'int'
B. class 'complex'
C. class 'float'
D. class 'str'
答案 D
第 4 题 单选题
在 Python 中,以下哪个选项可以用来遍历一个字典的键和值?( )
A.for key, value in dict.items()
B.for key, value in dict.keys_values()
C.for key, value in dict.iter()
D.for key, value in dict.loop()
答案 A
第 5 题 单选题
在 Python 中,以下哪个选项用于获取一个文件的大小?( )
A. os.path.size()
B. os.path.getsize()
C. os.path.length()
D. os.path.filesize()
答案 B
二、编程题
第 6 题 问答题
编程实现:
给定一个字符,连续输出 3 个该字符。
例如:字符为 A ,连续 3 个字符为 AAA 。
输入描述:
输入一个字符
输出描述:
输出连续 3 个该字符(字符之间没有空格)
样例输入:
A
样例输出:
AAA
答案:
python
letter = input()
res = letter *3
print(res)第 7 题 问答题
编程实现:
给定一个字符串 S ( 3≤S 长度 ≤1000 ),输出字符串 S 的最后两个字符。
例如: S ="abcd" , abcd 最后两个字符为 "cd" ,则输出 cd 。
输入描述:
输入一个字符串 S ( 3≤S 长度 ≤1000 )
输出描述:
输出一个字符串,表示字符串 S 的最后两个字符
样例输入:
abcd
样例输出:
cd
答案:
python
s = input()
res = s[-2:] #从倒数第2个字符到最后
print(res)第 8 题 问答题
编程实现:
给定一个正整数 N ( 100≤N≤1000000 ),分别将 N 中奇数位上的数字相加,偶数位上的数字相加,最后将两个相加的和相乘,并输出相乘的结果(奇数位包含个位、百位、万位、百万位,偶数位包含十位、千位、十万位)。
例如: N=1234 ,奇数位上的数字为 4 、 2 ,相加的和为 6 ;偶数位上的数字为 3 、 1 ,相加的和为 4;最后相乘的结果为 24 ( 24=64 )。
输入描述:
输入一个正整数 N ( 100≤N≤1000000 )
输出描述:
输出一个整数,表示奇数位和与偶数位和相乘的结果
样例输入:
1234
样例输出:
24
答案:
python
n = input()
n = n[::-1]
odds,evens = 0,0 #奇数和,偶数和
for i in range(len(n)):
#0--1
j = i+1
if j%2==1:
odds += int(n[i])
else:
evens += int(n[i])
print(odds*evens)第 9 题 问答题
编程实现:
有 1 个细胞,从第二天开始,它每天早上会分裂出 1 个新的细胞(分裂这天算新细胞的第一天)。每个新分
裂的细胞从它出生的第 3 天开始,每天早上也会分裂出 1 个细胞。
请计算出到第 N ( 2≤N≤30 )天晚上共有多少个细胞(假设细胞不会死亡)。
例如: N = 5 ,第 5 天晚上共有 8 个细胞。

输入描述:
输入一个正整数 N ( 2≤N≤30 )
输出描述:
输出一个整数,表示到第 N 天晚上细胞的总个数
样例输入:
5
样例输出:
8
答案:
python
n = int(input())
if n==1:
res = 1
elif n==2:
res = 2
else:
a = 1
b = 2
for x in range(3,n+1):
c = a + b
a = b
b = c
res = c
print(res)第 10 题 问答题
编程实现:
在一个 M 行 N 列的网格中放有若干个坚果(一个小格子里最多放一个坚果),第 X 行 Y 列的小格子是小松鼠的家。
小松鼠可以向上下左右的格子移动寻找坚果,但它每次从家出发后,最多可以移动 K 个小格子,发现格子中有坚果,就会将其运回家储藏起来(运回家所移动的格子不做计算),然后再从家出发寻找其他坚果。小松鼠最多可以储藏几个坚果。
例如: M=7 , N=6 , X=3 , Y=4 , K=3 ,在 7 行 6 列的网格中有若干个坚果(如下图),小松鼠的家在第3 行,第 4 列的位置,最多可以移动 3 个小格。 
小松鼠最多可以储藏 7 个坚果(小格子底色为绿色的坚果)。
输入描述:
第一行输入两个正整数 M 和 N ( 2≤M≤30 , 1≤N≤30 ),表示 M 行 N 列的网格,两个正整数之间以一个英文逗号隔开;
第二行输入两个正整数 X 和 Y ( 1≤X≤M , 1≤Y≤N ),表示小松鼠家的位置在第 X 行第 Y 列,两个正整数之间以一个英文逗号隔开;
第三行输入一个正整数 K ( 1≤K≤max(M, N)-1),表示小松鼠从家出发后,最多可以移动的小格子数第四行开始,输入 M 行,每行 N 个整数,除了第 X 行 Y 列的小格子用 2 表示小松鼠的家,其他小格子的整数只能是0 或者 1 。 0 表示小格子中没有坚果, 1 表示小格子中有 1 个坚果,整数之间以一个英文逗号隔开。
输出描述:
输出一个整数,表示小松鼠最多可以储藏的坚果数量。
样例输入:
7,6
3,4
3
0,0,1,0,1,0
0,0,0,0,1,0
0,1,0,2,0,0
1,0,0,1,0,1
0,0,1,0,0,0
0,0,0,0,0,1
1,0,0,1,0,0
样例输出:
7
答案:
python
m,n = list(map(int,input().split(',')))
sx,sy = list(map(int,input().split(','))) #松鼠的位置 sx所在行,sy列
sx,sy = sx-1,sy-1
max_steps = int(input())
lst =[]
for row in range(m):
new_line = list(map(int,input().split(',')))
lst.append(new_line)
res = 0
#遍历二维列表:从上到下,从左到右
for x in range(m):
for y in range(n):
dxy= abs(sx-x) + abs(sy-y)
if dxy <= max_steps and lst[x][y]==1:
res +=1
print(res)第 11 题 问答题
编程实现:
蚂蚁王国住着 N 只蚂蚁,每只蚂蚁都有自己的领地,领地之间可以直接到达或经过其他领地间接到达,可以 直接到达的领地之间的道路距离都为 1 ,但所有领地都有一条唯一的最短路径可以相互到达。
现要在 N 块领地(依次编号为 1~N)中,选出一块领地建立游乐场,使得所有蚂蚁到游乐场的最小距离总和 是 N 种情况中最小的。
例如: N = 8 , 1~8 号领地之间的连接关系为: 1 和 5 、 2 和 6 、 3 和 6 、 4 和 5 、 5 和 6 、 4 和 7 、 5 和 8 。
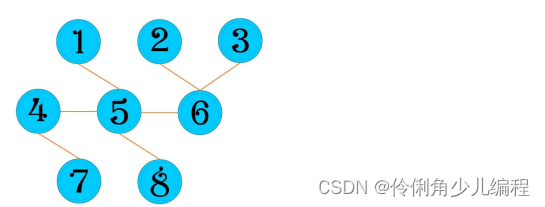
如果将游乐场创建在 5 号领地,最小距离总和为 10 。
1 号到 5 号距离为 1 ; 2 号到 5 号距离为 2 ; 3 号到 5 号距离为 2 ; 4 号到 5 号距离为 1 ; 6 号到 5 号距离为 1 ;
7 号到 5 号距离为 2 ; 8 号到 5 号距离为 1 。
如果将游乐场创建在 6 号领地,最小距离总和为 12 。
1 号到 6 号距离为 2 ; 2 号到 6 号距离为 1 ; 3 号到 6 号距离为 1 ; 4 号到 6 号距离为 2 ; 5 号到 6 号距离
为 1 ;
7 号到 6 号距离为 3 ; 8 号到 6 号距离为 2 。
......
可以发现,将游乐场创建在 5 号领地,最小距离总和 10 是最小的,故输出 10 。
输入描述:
第一行输入一个正整数 N ( 2≤N≤20 ),表示领地数量
接下来输入 N-1 行,每行包含两个正整数( 1≤ 正整数 ≤N ,两个正整数不相同),表示两块领地相互之间可以
直接到达,正整数之间以一个英文逗号隔开(数据保证 N 块领地相互之间可以到达)
输出描述:
输出一个整数,表示 N 种情况中最小距离总和的最小值
样例输入:
8
1,5
2,6
3,6
4,5
5,6
4,7
5,8
样例输出:
10
答案:
python
n = int(input())
ws = []
for x in range(n-1):
path = list(map(int,input().split(',')))
ws.append(path)
def findConnect(p):
lst = []
for i in range(n-1):
if p in ws[i]:
#p, a+b-p :left
np = sum(ws[i])-p
if visited[np]==False:
lst.append(np)
return lst #返回这个节点的下一层节点,放在列表中
def cost(p,cnt): #计算从节点p到它所有的子节点成本和
nodes = findConnect(p)
if len(nodes)==0:
return 0
visited[p] = True
res = 0
for node in nodes:
res = res + cost(node,cnt+1) +cnt
return res
ans=[]
for x in range(1,n+1):
visited = [False]*(n+1)
res = cost(x,1)
ans.append(res)
print(min(ans))