最近公共祖先

wlwhonest2024-07-08 14:26

最近公共祖先

方法：

  1. 向上标记法 O ( n ) O(n) O(n)
  2. 倍增
  • f a [ i , j ] fa[i,j] fa[i,j]表示从i开始，向上走 2 j 2^j 2j步所能走到的节点。 0 < = j < = l o g ( n ) 0<=j<=log(n) 0<=j<=log(n), d e p t h [ i ] depth[i] depth[i]表示深度
    • [1]先将两个点跳到同一层
    • [2]让两个点同时往上跳，一直跳到它们的最近公共祖先的下一层。
  • 预处理时间复杂度: O ( n l o g ( n ) ) O(nlog(n)) O(nlog(n))
  • 查询复杂度: O ( l o g ( n ) ) O(log(n)) O(log(n))
  1. tarjan------离线求LCA( O ( n + m ) O(n+m) O(n+m))

马上要caip省赛，应该还来得及

题单

1.祖孙询问

公共祖先要考虑深度，所以需要depth[N]

纯裸的一道lca题目

c 复制代码 
#include<bits/stdc++.h>

using namespace std;
int n,m;
const int N=4e4+10,M=2*N;
int h[N],e[M],ne[M],idx;
int depth[N],fa[N][16],q[N];

void add(int a,int b){
  e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void bfs(int root){
  memset(depth,0x3f,sizeof depth);
  depth[0]=0,depth[root]=1;
  int hh=0,tt=1;
  q[0]=root;
  while(hh<tt){
    int t=q[hh++];
    //if(hh==N) hh=0;
    
    for(int i=h[t];i!=-1;i=ne[i]){
      int j=e[i];
      if(depth[j]>depth[t]+1){
        depth[j]=depth[t]+1;
        fa[j][0]=t;
        
        q[tt++]=j;
        //if(tt==N) tt=0;
				
        for(int k=1;k<=15;k++){
          fa[j][k]=fa[fa[j][k-1]][k-1];
        }
      }
    }
  }
}

int lca(int a,int b){
  
  if(depth[a]<depth[b]) swap(a,b);
  for(int i=15;i>=0;i--){
    if(depth[fa[a][i]]>=depth[b]){
       a=fa[a][i];
    }
  }
  if(a==b) return a;
  for(int i=15;i>=0;i--){
    if(fa[a][i]!=fa[b][i]){
      a=fa[a][i];
      b=fa[b][i];
    }
  }
  return fa[a][0];
}

signed main(){
  cin>>n;
  int root=0;
  memset(h,-1,sizeof h);
  for(int i=0;i<n;i++){
    int a,b;
    cin>>a>>b;
    if(b==-1) root=a;
    else{
      add(a,b);
      add(b,a);
    }
  }
  bfs(root);
  cin>>m;
  for(int i=0;i<m;i++){
    int a,b;
    cin>>a>>b;
    int res=lca(a,b);
    if(res==a) puts("1");
    else if(res==b) puts("2");
    else puts("0");
  }
  return 0;
}
2.距离

大模拟一遍这道题就能把tarjan算法搞清楚了

c 复制代码 
#include<bits/stdc++.h>

using namespace std;
int n,m;
typedef pair<int,int> PII;
const int N=1e4+10,M=2*N+10;
int h[N],e[M],ne[M],w[M],idx;
int p[N],st[N],dist[N];
int res[M];
vector<PII> query[N];

int find(int x){
  if(x!=p[x]) p[x]=find(p[x]);
  return p[x];
}

void add(int a,int b,int c){
  e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

//深搜，预处理根节点到其他节点的距离
void dfs(int u,int fa){
  
  for(int i=h[u];i!=-1;i=ne[i]){
    int j=e[i];
    if(j!=fa){
      dist[j]=dist[u]+w[i];
    	dfs(j,u);
    }
  }
}

//深搜在每个点做targan，然后更新已经回溯的节点并且被询问到的节点到当前节点的距离；
void tarjan(int u){
  st[u]=1;
  for(int i=h[u];i!=-1;i=ne[i]){
    int j=e[i];
    if(!st[j]){
      st[u]=1;
      tarjan(j);
      p[j]=u;
    }
  }
  
  for(auto item : query[u]){
    int y=item.first,id=item.second;
    if(st[y]==2){
      int anc=find(y);
      res[id]=dist[u]+dist[y]-2*dist[anc];
    }
  }
  st[u]=2;
}

			
signed main(){
  cin>>n>>m;
  memset(h,-1,sizeof h);
  for(int i=1;i<=n;i++) p[i]=i;
  for(int i=0;i<n-1;i++){
    int a,b,c;
    cin>>a>>b>>c;
    add(a,b,c);
    add(b,a,c);
  }
  for(int i=0;i<m;i++){
   	int a,b;
    cin>>a>>b;
    query[a].push_back({b,i});
    query[b].push_back({a,i});
  }
  
  dfs(1,-1);
  tarjan(1);
  
  for(int i=0;i<m;i++) cout<<res[i]<<endl;
  return 0;
}
3.次小生成树

思考：

  1. 为什么会和最近公共祖先有关

步骤：

  • 先kruskal算法求出最小生成树权值之和
  • 预处理一遍在最小生成树里的边的depth[i]和 f a [ i ] [ j ] fa[i][j] fa[i][j]
  • lca处理枚举最小生成树外的一条边加进最小生成树中产生的环，算出该环的最大边和次大边，进而判断该附加边是否的加入以及最大边(次大边)的移除是否会产生次小生成树，枚举最小生成树外的一条边就可以找到严格的次小生成树
c 复制代码 
#include<bits/stdc++.h>

using namespace std;
typedef long long LL;
int n,m;
const int N=1e5+10,M=3e5+10,INF=0x3f3f3f3f;
int h[N],e[M],ne[M],w[M],idx;
int p[N],dist[N],st[N],q[N];
int depth[N],fa[N][17];
int	d1[N][17],d2[N][17];

int find(int x){
  if(x!=p[x]) p[x]=find(p[x]);
  return p[x];
}
  
struct edge{
  int a,b,c;
  bool used;
  bool operator<(const edge& M)const{
    return c<M.c;
  }
}es[M];

void add(int a,int b,int c){
  e[idx]=b,w[idx]=c,ne[idx]=h[a],h[a]=idx++;
}

LL kruskul(){
  LL sum=0;
  sort(es,es+m);
  for(int i=0;i<m;i++){
    int a,b,c;
    a=es[i].a,b=es[i].b,c=es[i].c;
    int x=find(a),y=find(b);
    if(x!=y){
      p[x]=y;
      sum+=c;
      es[i].used=1;
    } 
  }
  return sum;
}

void build(){
 	memset(h,-1,sizeof h);
  for(int i=0;i<m;i++){
    if(es[i].used){
      int a=es[i].a,b=es[i].b,c=es[i].c;
      add(a,b,c);
      add(b,a,c);
    }
  }
}

void bfs(){
  
  memset(depth,0x3f,sizeof depth);
  depth[0]=0,depth[1]=1;
  q[0]=1;
  int hh=0,tt=1;
  while(hh<tt){
    int t=q[hh++];
    
    for(int i=h[t];i!=-1;i=ne[i]){
      int j=e[i];
      if(depth[j]>depth[t]+1){
        depth[j]=depth[t]+1;
        q[tt++]=j;
        fa[j][0]=t;
        
        d1[j][0]=w[i],d2[j][0]=-INF;
        
        for(int k=1;k<=16;k++){
          int anc=fa[j][k-1];
          fa[j][k]=fa[anc][k-1];
          int distance[4]={d1[j][k-1],d2[j][k-1],d1[anc][k-1],d2[anc][k-1]};
          d1[j][k]=d2[j][k]=-INF;
          for(int u=0;u<4;u++){
            int d=distance[u];
            if(d>d1[j][k]){
              d2[j][k]=d1[j][k];
              d1[j][k]=d;
              
            }
            else if(d!=d1[j][k]){
              if(d>d2[j][k]){
                d2[j][k]=d;
              }
            }
          }
        }
      }
    }
  }
}

int lca(int a,int b,int c){
  int distance[N*2];
  int cnt=0;
  if(depth[a]<depth[b]) swap(a,b);
  for(int i=16;i>=0;i--){
    //这里注意判断的是a的第2^i跳到的点的深度和b深度
    if(depth[fa[a][i]]>=depth[b]){
      distance[cnt++]=d1[a][i];
      distance[cnt++]=d2[a][i];
      a=fa[a][i];
    }
  }
  
  if(a!=b){
    for(int i=16;i>=0;i--){
      if(fa[a][i]!=fa[b][i]){
        distance[cnt++]=d1[a][i];
        distance[cnt++]=d2[a][i];
        distance[cnt++]=d1[b][i];
        distance[cnt++]=d2[b][i];
        a=fa[a][i];
        b=fa[b][i];
      }
    }
    distance[cnt++]=d1[a][0];
    distance[cnt++]=d1[b][0];
  }
  
  int dist1=-INF,dist2=-INF;
  for(int i=0;i<cnt;i++){
    if(dist1<distance[i]){
      dist2=dist1;
      dist1=distance[i];
    }
    else if(dist1!=distance[i]&&distance[i]>dist2){
      dist2=distance[i];
    }
  }
  if(c>dist1) return c-dist1;
  if(c>dist2) return c-dist2;
  return INF;
}

signed main(){
  cin>>n>>m;
  for(int i=1;i<=n;i++) p[i]=i;
  for(int i=0;i<m;i++){
    int a,b,c;
    cin>>a>>b>>c;
    es[i]={a,b,c};
  }
  LL sum = kruskul();
  build();
  bfs();
  LL res=1e18;
  for(int i=0;i<m;i++){
    if(!es[i].used){
      int a=es[i].a,b=es[i].b,c=es[i].c;
      res=min(res,sum+lca(a,b,c));
    }
  }
  //cout<<sum<<endl;
  cout<<res<<endl;
  return 0;
}
4.闇の連鎖
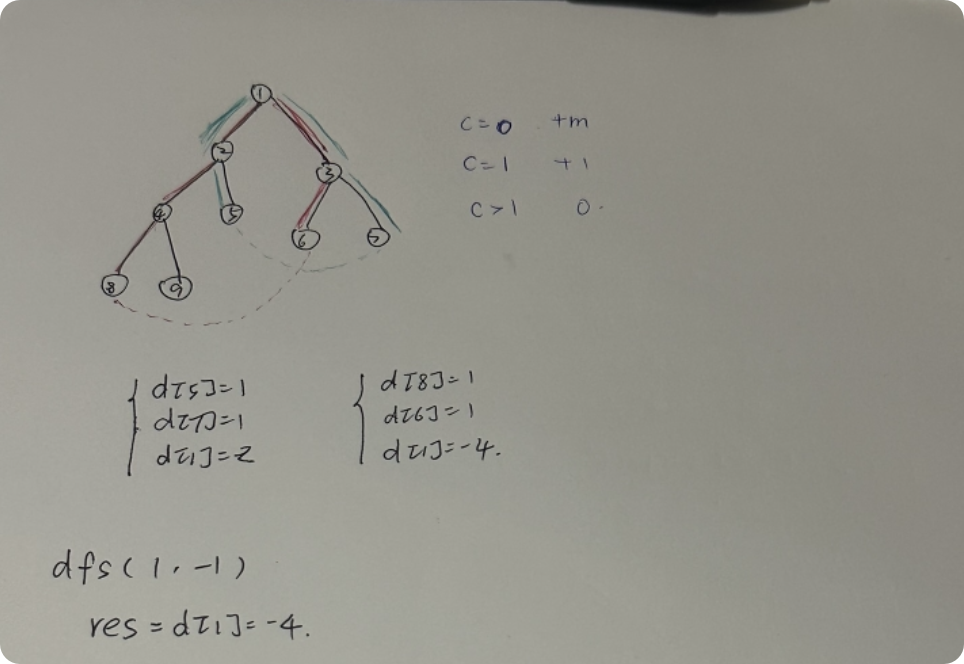
c 复制代码 
#include<bits/stdc++.h>

using namespace std;
int n,m;
const int N=1e5+10,M=2e5+10;
int h[N],e[M],ne[M],w[M],idx;
int d[N],depth[N],fa[N][17],q[N];
int ans;

void add(int a,int b){
  e[idx]=b,ne[idx]=h[a],h[a]=idx++;
}

void bfs(){
  memset(depth,0x3f,sizeof depth);
  depth[0]=0,depth[1]=1;
  int hh=0,tt=1;
  q[0]=1;
  
  while(hh<tt){
    int t=q[hh++];
    
    for(int i=h[t];i!=-1;i=ne[i]){
      int j=e[i];
      if(depth[j]>depth[t]+1){
        depth[j]=depth[t]+1;
        q[tt++]=j;
        fa[j][0]=t;
        
        for(int k=1;k<=16;k++){
          int anc=fa[j][k-1];
          fa[j][k]=fa[anc][k-1];
        }
      }
    }
  }
}

int lca(int a,int b){
  if(depth[a]<depth[b]) swap(a,b);
  for(int k=16;k>=0;k--){
    if(depth[fa[a][k]]>=depth[b]){
      a=fa[a][k];
    }
  }
  if(a==b) return a;
  if(a!=b){
    for(int k=16;k>=0;k--){
      if(fa[a][k]!=fa[b][k]){
        a=fa[a][k];
        b=fa[b][k];
      }
    }
  }
  return fa[a][0];
}

int dfs(int u,int father){
  int res=d[u];
  
  for(int i=h[u];i!=-1;i=ne[i]){
    int j=e[i];
    if(j!=father){
      int s=dfs(j,u);
      if(s==0) ans+=m;
      if(s==1) ans+=1;
      res+=s;
    }
  }
  return res;
}

signed main(){
  memset(h,-1,sizeof h);
  cin>>n>>m;;
  for(int i=0;i<n-1;i++){
    int a,b;
    cin>>a>>b;
    add(a,b);
    add(b,a);
  }
  bfs();//先预处理出每一条，才能求lca啊老铁
  for(int i=0;i<m;i++){
    int a,b;
    cin>>a>>b;
    int p=lca(a,b);
    d[a]++,d[b]++,d[p]-=2;
  }
  
  
  dfs(1,-1);
  cout<<ans<<endl;
  return 0;
}
相关推荐
无限大.2 分钟前
c语言实例
c语言·数据结构·算法
六点半8887 分钟前
【C++】速通涉及 “vector” 的经典OJ编程题
开发语言·c++·算法·青少年编程·推荐算法
@haihi15 分钟前
冒泡排序，插入排序，快速排序，选择排序
数据结构·算法·排序算法
quaer18 分钟前
Open-Sora全面开源?
开发语言·算法·机器学习·matlab·矩阵
Hello.Reader30 分钟前
TopK算法在大数据重复数据分析中的应用与挑战
大数据·算法·数据分析
coduck_S12004zbj33 分钟前
csp-j模拟五补题报告
c++·算法·图论
洛临_39 分钟前
【C语言】基础篇
c语言·算法
_.Switch1 小时前
Python机器学习模型的部署与维护：版本管理、监控与更新策略
开发语言·人工智能·python·算法·机器学习
自由的dream2 小时前
0-1背包问题
算法
2401_857297912 小时前
招联金融2025校招内推
java·前端·算法·金融·求职招聘
热门推荐
01组基轨迹建模 GBTM的介绍与实现（Stata 或 R）02【经验分享】Ubuntu22.04安装微信(linux官方版)032024年高教社杯数学建模国赛C题超详细解题思路分析04分享几个惊艳的 Three.js 个人站点05安卓系列机型永久去除data分区加密 详细步骤解析06【2024数模国赛赛题思路公开】国赛B题思路丨附可运行代码丨无偿自提07CTF网络安全大赛简单的web抓包题目：HEADache08Ubuntu24.04安装中文输入法09【2024高教社杯全国大学生数学建模竞赛】B题 生产过程中的决策问题——解题思路 代码 论文10springer 在线投稿编译踩坑