目录
[1 栈](#1 栈)
[2 队列](#2 队列)
[3 deque 介绍](#3 deque 介绍)
[4 优先级队列](#4 优先级队列)
[5 反向迭代器](#5 反向迭代器)
栈也是我们在C语言就模拟实现过的一种数据结构,在C++中,栈其实和我们前面模拟实现过的string、vector等容器有一点区别,站起是不是容器,而是一种容器适配器,我们可以打开C++官方文档找到stack的介绍来看一下
同时我们打开队列的文档就会发现,队列也是一种容器适配器,

那么适配器到底是什么东西呢?适配器其实是一种设计模式,是一套被反复使用、多数人知晓的、经过分类编目的、代码设计经验的总结。使用设计模式是为了可重用代码、让代码更容易被他人理解、保证代码可靠性、程序的重用性。
在前面的容器的模拟实现中,困扰我们颇多的迭代器也是一种设计模式。而适配器是设计模式中结构模式中的一种。 适配器本质上是进行转换的,使用现有的东西封装转换成你想要的东西。
1 栈
我们说栈是一种容器适配器,而适配器的本质是进行转换。
我们发现栈的结构很少,因为他的结构限制了他的接口,而在之前C语言我们实现栈使用一个动态顺序表来实现的,因为栈的接口其实就相当于顺序表的尾插尾删,使用数组完成效率很高,这其实就是一种转换,我们将顺序表通过封装接口转换出我们想要的栈。而在C++中,我们也能够使用前面模拟实现过的 vector 和 list 来作为栈的适配容器,具体使用哪个其实都行,在栈的实现上,它们各有千秋,而我们看到的库里面的栈的默认适配容器则是一个双端队列 deque
这个容器我们还没学过,在栈和队列后面会讲一下。
目前我们实现栈就使用vector来作默认容器,因为其实 vector 实现栈的效率其实跟deuqe差不多的。栈的基本的结构如下,就是一个vector,然后封装vector的接口来实现栈的接口


栈的构造函数只有一个,而这个构造函数我们直接理解为无参的构造就行了,这里的缺省值的意思其实就是可以使用我们的适配器容器的对象来初始化,但是我们一般实现栈是不需要这样初始化的。
既然是一个无参构造,那么我们需要自己写吗?不需要,因为编译器自动生成的就够用了,栈对象中只有一个我们实现过的vector的对象,而我们实现过的vector是有默认构造的,那么编译器自动生成构造函数就会去调用vector的默认构造去对st进行初始化。那么析构也是一样的,我们也不需要自己去实现。
那么剩下的几个接口 size 、empty 、top 、 push 、pop就很简单了。
bool empty()const
{
return st.empty();
}
size_t size()const
{
return st.size();
}
T& top()
{
assert(!empty());
return st.back();
}
const T& top()const
{
assert(!empty());
return st.back();
}
void push(const T& val)
{
st.push_back(val);
}
void pop()
{
assert(!empty());
st.pop_back();
}这样一来,一个简单的栈就实现了。栈是不需要实现迭代器的,因为不需要,对于栈而言,遍历整个栈就是需要用户不断地取top,然后pop,而不是像容器一样通过迭代器遍历。
2 队列
队列是先入先出的结构,也就是头插和头删,尾插头删vector的效率就不如list了,所以我们实现queue使用list作为默认容器。

其他的接口也基本上和stack差不多
bool empty()const
{
return q.empty();
}
size_t size()const
{
return q.size();
}
const T& front()const
{
assert(!empty());
return q.front();
}
const T& back()const
{
assert(!empty());
return q.back();
}
void push(const T& val)
{
q.push_back(val);
}
void pop()
{
assert(!empty());
q.pop_front();
}3 deque 介绍
为什么stack和queue的默认适配容器都是 deque 双端队列呢?deque到底是何方神圣?
在介绍 deque之前,我们先回想一下vector和list都有什么缺点。vector的缺点就是扩容的开销大,因为他的扩容需要挪动数据,同时他的头插头删的开销也很大,不适合作为队列的适配容器。 而list的缺点则是不支持随机访问,同时由于空间不连续,他的CPU高速缓存命中率低。
那么能不能设计一个容器,能够完美融合vector和list的优点,同时能够规避他们的缺点呢?从结果上来说,肯定是没有的,如果有容器能够完美替代vector和list,如今我们也不会学习这两个容器了,早就被湮没在历史中。双端队列就是一个兼具 vector 和 list 的优点的一个容器 ,比如他的头插头删效率高,cpu命中率高等,但是他的这些性能都比不上单独拎出来的 list 和vector,相当于不上不下的水平,list 和vector在各自的领域是极致效率的,而deque的效率最多只能用拔尖来描述,比不上list 和vector。
deque是怎么做到既适合头插头删,同时cpu命中率还高的呢?这就要从它的结构说起了。
deque其实是由一个一个的数组来构成的,同时 deque 内部存储了一个指针数组,来保存些数组的地址。
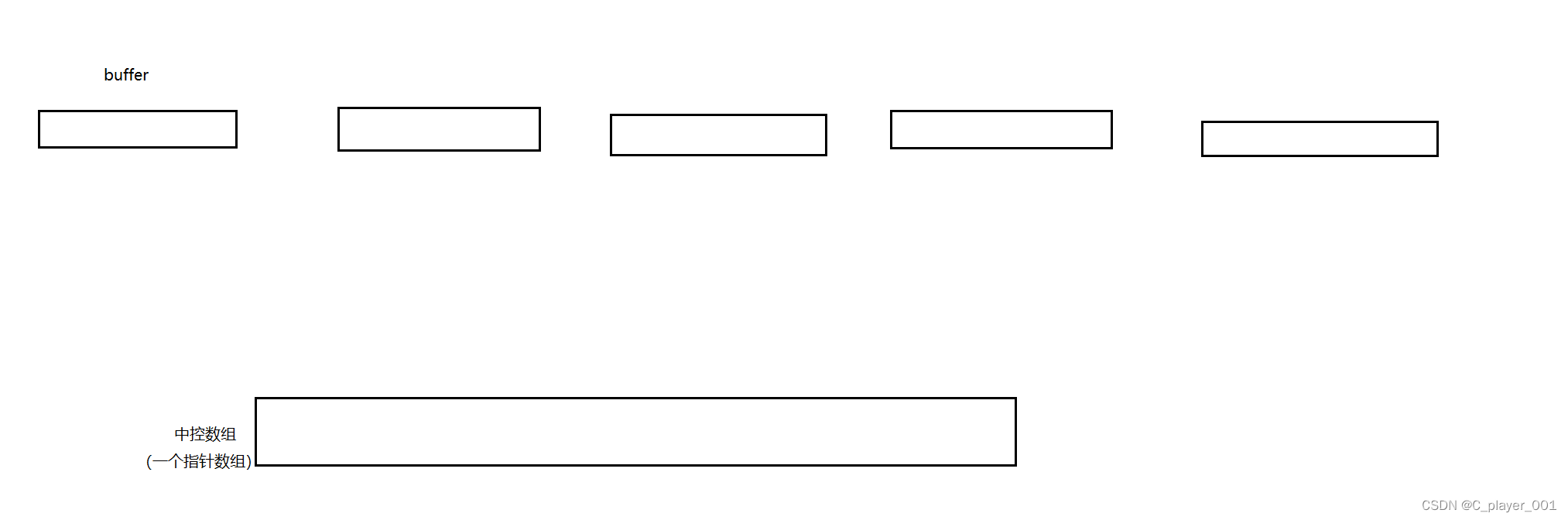
当我们第一次插入数据时,首先申请一个数组buffer,buffer的大小是由我们自己来指定的静态数组。 第一个申请的数组的指针保存在 中控数组的中间位置上
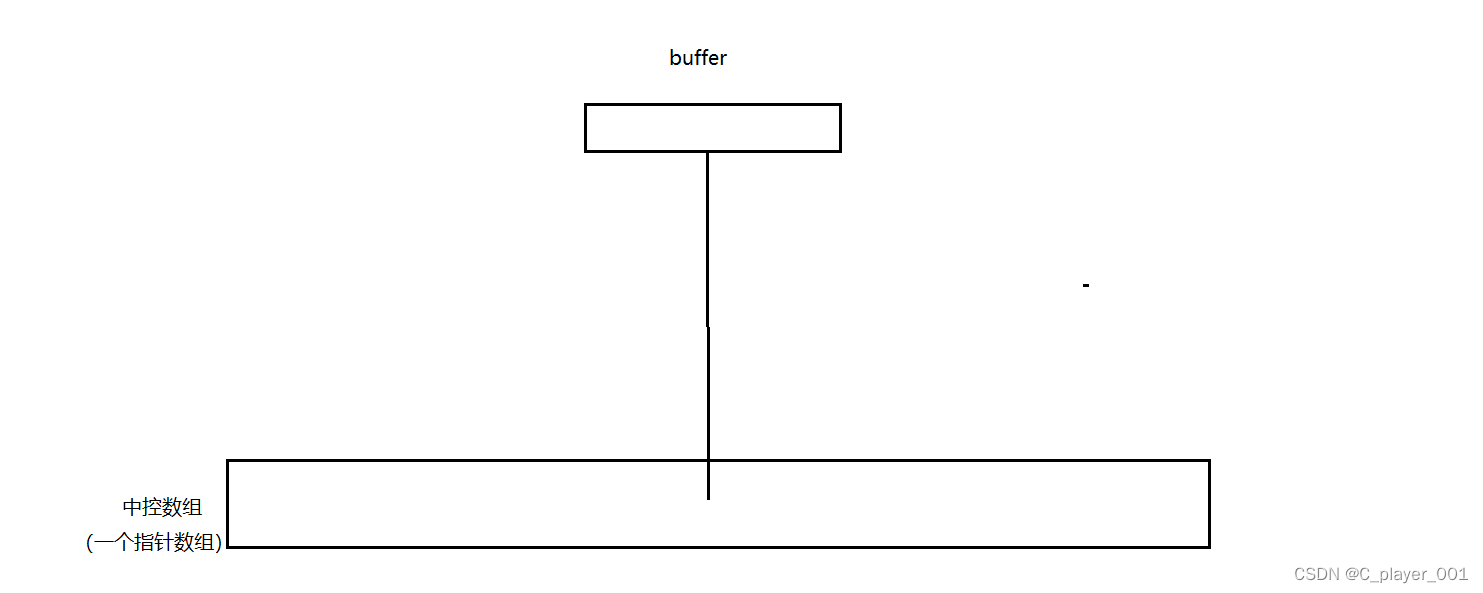
而当我们不断尾插数据时,数组的尾部进行插入,如果数组满了,再次尾插,则会再开辟一个同样大小的数组,将数组的地址保存在中控数组的后一个位置

依次类推,当尾插到一定数量时,中控数组的后半部分都已经被填满了,这时候就会被中控数组进行二倍扩容
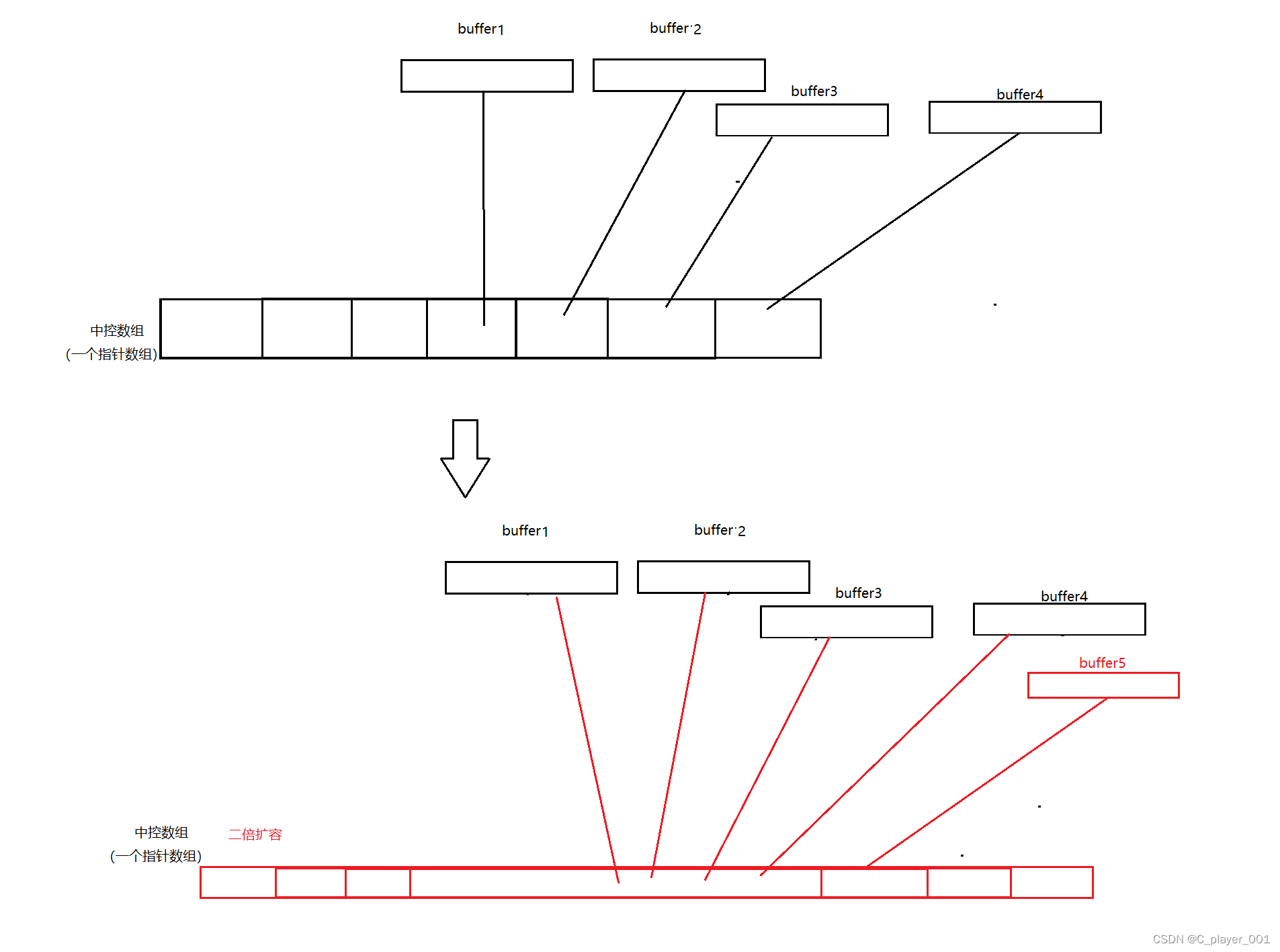
扩容之后会将原中控数组保存的指针全部拷贝到新的数组中,同时不会释放原来的 buffer ,再创建一个新的buffer来存储新插入的数据。 所以说,deque其实也是有扩容的消耗的,只是他的消耗相比于vector来说要小得多,它只需要挪动指针数组就行了。
而如果要头插的话,则需要在中控数组的中间位置的前面填充新创建的buffer的指针,然后将新的数组从专门用于头插的 buffer 的尾部开始插入,不断往前插入,过程基本类似于尾插。
而deque支持的随机访问则需要在 [ ]重载的时候进行一定的运算转换来找到对用下标的数据,所以他的随机访问的效率其实也是不如vector的。
同时,我们也能发现一个问题,就是deque在进行中间位置的插入删除的话会很复杂,如果要插入或者删除的数据个数刚好是 buffer 大小的整数倍还好说,如果不是整数倍,则要比 vector 和list 麻烦的多,所以其实deque的任意位置插入删除的效率也是比不上 list 的
但是这其实也是它的优势所在,他进行除了中间位置插入删除之外的其他的操作的操作都还不错,我们知道 queue 和stack是不需要中间位置的插入删除的,所以由 deque 作为 stack 和 queue 的默认适配容器刚刚好,很通用。
如果要模拟实现 deque ,最复杂的其实还不是他的下标转换以及他的中间位置的插入删除,而是他的迭代器的实现,他的迭代器的实现需要四个指针来实现,具体的实现大家可以在网上查阅相关资料,总之十分的复杂,简直折磨人 。我们只需要知道她大概的实现就OK了,最重要的就是中控数组也就是一个指针数组就行了。
4 优先级队列
优先级队列其实就是把优先级最高的或者优先级最低的数据放在第一个,那么之前我们有没有学过类似的结构呢? 学过,就是我们的堆。 大堆就是把最大的数放在堆顶,也就是优先级最高的数据放在最前面,而小堆就是把优先级最小的数据放在最前面。而我们以前实现了堆,他的物理结构其实是一个数组,也就是一个vector,而他的逻辑结构我们看成是一棵完全二叉树。
那么优先级队列的默认适配容器我们就能够使用vector来实现。同时,虽然他叫做优先级队列,但是他的本质上还是一个堆,同时他也只能够读取头部数据以及头删,他的插入是需要进行调整来保证堆结构的。
我们可以看一下库里面的优先级队列的模板参数,我们发现模板参数除了我们意料之中的数据类型,适配容器,还有一个 less<...> ,这个less< >相信我们在leetcode刷题的时候或者我们使用sort的时候也经常使用。

我们先不管这个less 仿函数,假设我们就用 vector 实现一个大堆,实现完之后我们再将仿函数加上。

他的接口中,默认的构造和析构编译器自动生成的就够用,不需要我们自己写。而 empty ,size 和top接口实现起来也十分简单,
public:
bool empty()const
{
return pq.empty();
}
size_t size()const
{
return pq.size();
}
const T& top()const
{
assert(!empty());
return pq[0];
}他的重点在插入和删除上,对于插入数据,以前我们使用堆的时候插入数据首先是插入在数组的最后,也就是尾插,然后通过向上调整来维持堆结构。我们可以写一下push和adjustup的实现
//push 就是尾插
void push(const T& val)
{
pq.push_back(val);
//然后向上调整
adjust(size()-1); //传新插入的数据的的下标
}
void adjust(size_t child)
{
size_t parent = (child - 1) / 2; //父节点的下标
while (child) //child 为 0 时退出循环
{
if (pq[child] >pq[parent]) //假设是建大堆、
{
swap(pq[child],pq[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}然后实现 pop ,pop 就是删除 栈顶元素,但是删除栈顶元素之后我们还需要通过向下调整来保证栈结构。
void pop()
{
swap(pq.front(),pq.back());
pq.pop_back();
adjustdown(0); //开始调整下标
}
//向下调整
void adjustdown(size_t parent)
{
size_t maxchild = parent*2+1;
while (maxchild<size())
{
if (maxchild + 1 < pq.size() && pq[maxchild + 1] > pq[maxchild]) //假设是大堆
maxchild++;
if (pq[parent] < pq[maxchild])
{
swap(pq[parent],pq[maxchild]);
parent = maxchild;
maxchild = parent*2 + 1;
}
else
break;
}
}这样一来就写好了弹出栈顶元素和向下调整的方法了。
最后再实现一个迭代器区间的构造函数,
这个函数还是要用到仿函数,但是我们在这里其实也可以不使用仿函数,因为我们可以直接复用adjustdown来进行向下调整建大堆,一会讲完了仿函数之后我们也只需要修改向下调整和向上调整的逻辑就行了,而不用修改这里的构造函数。
向下调整建大堆我们只需要找到第一个非叶子节点,然后往前遍历,让每一棵子树都是大堆就行了。至于为什么不用向上调整建大堆 可以 看一下我的数据结构专栏的堆的实现,是由于向下调整建堆的效率比向上调整建堆的效率是要高得多的,效率差距主要体现在叶子节点的向上调整中。
//默认构造
priority_queue()
{}
//迭代器区间构造
template<class InputIterator>
priority_queue(InputIterator first, InputIterator last)
:pq(first,last)
{
size_t end = (size() - 1 - 1) / 2;
while (end!=0)
{
adjustdown(end);
end--;
}
adjustdown(end);
}这里要注意的一点就是,如果我们写了迭代器区间的构造,那么编译器就不会自动生成默认构造函数了,我们需要自己实现一个默认构造,而这里的priority_queue的默认构造我们也什么都不用写,编译器会再初始化列表自动调用vector的默认构造来进行初始化,析构函数也是一样的,编译器自动生成的就能够完成析构了。
仿函数
实现完一个大堆,我们就要开始该清楚仿函数是什么东西,只有搞清楚了仿函数我们才能够实现一个完成的优先级队列。
仿函数其实就是一个类,这个类实例化出来的对象就叫仿函数,类里面重载了( ) 这个函数调用操作符。叫做仿函数的原因是这个类的对象可以像函数调用一样实现按我们的逻辑。
比如:
template<typename T>
class myless
{
public:
bool operator()(const T& x, const T& y)const
{
return x < y;
}
};这样一个类能够干什么呢?
我们使用 sort 的时候是不是有这样的用法
sort ( container :: iterator first , container :: iterator last , less<T> ( ) )
这里面的 less<T>() 就是一个仿函数,为什么这么说呢?参考我们上面实现的仿函数类, <T>表示数据类型是T,编译器在实例化出这个匿名对象的时候就会使用具体的 T 去实例化,然后用这个匿名对象的 ( ) 也就是 operator() 来传参,也就是将这个成员函数传给了 sort 。
vector<int> v;
v.push_back(5);
v.push_back(7);
v.push_back(4);
v.push_back(3);
v.push_back(9);
v.push_back(2);
vector<int>v1 = v;
sort(v.begin(),v.end(),myless<int>());
for (auto e : v)
{
cout << e << " ";
}
cout << endl;
sort(v1.begin(), v1.end(), less<int>());
for (auto e : v)
{
cout << e << " ";
}
cout << endl;我们可以看一下我们自己实现的的 myless 和库里面的 less 是不是一样的

其实仿函数的传参就有点类似于我们以前C语言传递函数指针,但是函数指针写起来很复杂,尤其是对于一些复杂的函数指针,同时函数指针也不支持泛型编程,每一个类型的比较都需要写一个函数来实现,但是仿函数他就是一个类实例化出来的对象,我们传参穿的也是这个对象,我们只需要显式传递数据类型,就能够实例化出我们想要的数据类型的比较函数。
上面的传参我们也可以使用一个有名对象来传参
myless<int> mless;
sort(v.begin(),v.end(),mless);我们以前的泛型都是类型的泛型,而这里的仿函数的泛型则是逻辑的泛型。
那么我们就可以用仿函数来完善我们的优先级队列了。
template<typename T ,typename container_type=vector<T>,typename CMP=less<T>>
void adjustup(size_t child)
{
CMP cmp;
size_t parent = (child - 1) / 2; //父节点的下标
while (child) //child 为 0 时退出循环
{
//if (pq[child] >pq[parent]) //假设是建大堆
if(cmp(pq[parent],pq[child]))
{
swap(pq[child],pq[parent]);
child = parent;
parent = (child - 1) / 2;
}
else
{
break;
}
}
}
//向下调整
void adjustdown(size_t parent)
{
CMP cmp;
size_t maxchild = parent*2+1;
while (maxchild<size())
{
//if (maxchild + 1 < pq.size() && pq[maxchild + 1] > pq[maxchild]) //假设是大堆
if (maxchild + 1 < pq.size() && cmp(pq[maxchild],pq[maxchild+1])) //假设是大堆
maxchild++;
//if (pq[parent] < pq[maxchild])
if (cmp(pq[parent] , pq[maxchild]))
{
swap(pq[parent],pq[maxchild]);
parent = maxchild;
maxchild = parent*2 + 1;
}
else
break;
}
}这还只是仿函数的基础用法,仿函数还有一些高级用法,比如我们要实现两个对象的大小的比较
class A
{
public:
A(int n = 0)
:_n(n)
{}
bool operator<(const A& a)const
{
return _n < a._n;
}
private:
int _n;
};我们首先要在该类中重载 < 运算符,然后创建两个对象进行比较
int main()
{
A a1(10);
A a2(20);
int ret = myless<A>()(a1,a2);
cout << ret << endl;
return 0;
}
目前来看没什么问题,但是当我们的对象是使用 new 申请的呢?这时候我们一般使用的就是对象的指针了,如果我们想要直接传这两个指针进行两个指针所指向的对象比较,目前我们实现的仿函数类是做不到的,
A* p1 = new A(20);
A* p2 = new A(10);
int ret = myless<A*>()(p1,p2);
cout << ret << endl;我们只能这么用,而且这样比较出来的结果还不一定是对的,因为这样比较的话,比较的是两个指针的大小,而不是对象的大小了,但是我们就是想要比较类对象的大小要怎么做呢?
很简单,我们只需要在仿函数类中再重载一个( )函数就行了.
bool operator<(const A& a)const
{
return _n < a._n;
}这样一来,如果我们传的是A类型的指针,我们也可以直接使用 myless<A>的仿函数进行比较
A* p1 = new A(20);
A* p2 = new A(10);
int ret = myless<A>()(p1,p2);
cout << ret << endl;我们这里举例的例子其实用的不是很合适,更恰当的例子是类似于一个排序算法的场景,既要支持对象本身的比较,还要支持参数是对象指针时对指针所指向的对象的比较。
5 反向迭代器
为什么我们前面没实现反向迭代器,因为反向迭代器其实就是一种适配器,为什么这么说呢?我们知道,反向迭代器和正向迭代器唯一的区别就是 ++ 和 -- 的方向,正向迭代器 ++ 是从前往后走 ,而反向迭代器的 ++ 是从后往前走,所以要实现反向迭代器我们只需要封装和复用正向迭代器的代码,就能够很轻松的实现。
拿 list 的反向迭代器来举例,反向迭代器的 rbegin() 和 rend() 的位置是哪呢?
我们可以向正向迭代器一样,让 rbegin 指向最后一个节点,也就是在迭代器中维护 phead->prev ,然后rend 指向第一个节点的前一个节点,也就是 phead ,这样是一个标准的反向迭代器,但是这样却没有最大程度的复用正向迭代器。 让 rbegin 直接复用 正向迭代器的 end ,让rend 直接复用 begin ,但是这样设计有一个要注意的地方就是,解引用的时候 ,要返回的不是当前指针指向的节点的数据,而是当前节点的建一个节点的数据,因为我们相当于 将区间整体往右移了一个节点。 还有就是要实现 反向迭代器的 ++ ,我们就需要正向迭代器中重载了 - - ,要实现 - - ,则需要复用正向迭代器的 ++ 。
那么反向迭代器的实现就很简单了,下面是一个针对 list 的反向迭代器的简单的实现,可能会有一些问题,但是大体的框架就是这样了。
template<typename T, typename ref, typename ptr>
class reverse_list_iterator
{
public:
typedef _list_iterator<T> _list_iterator;
//迭代器的构造
reverse_list_iterator(_list_iterator it)
:_it(it)
{
}
reverse_list_iterator& operator++()
{
return --_it;
}
reverse_list_iterator& operator++(int) //后置++
{
return _it--;
}
bool operator!=(reverse_list_iterator& it1)const
{
return _it!=it1._it;
}
ref operator*()
{
list_iterator tmp=_it;
--tmp;
return *tmp;
}
const T& operator*()const
{
list_iterator tmp = _it;
--tmp;
return *tmp;
}
ptr operator->()
{
return _it.operator->();
}
listnode* pnode;
private:
_list_iterator _it;
};但是,其实反向迭代器不是针对某一个容器来设计的,他的重点在于复用,能够用不同类型的正向迭代器,来转换出相应的反向迭代器。
template<typename Iterator>但是这里面需要用到一些牛逼的技术来实现 从 正向迭代器中提取出 ref 和 ptr 用于 * 和 -> 的返回类型。