在之前的文章中,我们使用WebGL绘制了很多二维的图形和图像,在学习2D绘图的时候,我们提过很多次关于GPU的高效渲染,但是2D图形的绘制只展示了WebGL部分的能力,WebGL更强大的地方在于,它可以绘制各种3D图形,而3D图形能够极大地增强可视化的表现能力。
相信很多小伙伴都对此有所耳闻,也有不少人学习WebGL,就是冲着它的3D绘图能力。
接下来,我就用一个简单的正立方体的例子来演示在WebGL中如何绘制3D物体。
从二维到三维
首先,我们先来绘制一个熟悉的2D图形,正方形。
// vertex
attribute vec2 a_vertexPosition;
attribute vec4 color;
varying vec4 vColor;
void main() {
gl_PointSize = 1.0;
vColor = color;
gl_Position = vec4(a_vertexPosition, 1, 1);
}
// fragment
#ifdef GL_ES
precision highp float;
#endif
varying vec4 vColor;
void main() {
gl_FragColor = vColor;
}
// ...
renderer.setMeshData([{
positions: [
[-0.5, -0.5],
[-0.5, 0.5],
[0.5, 0.5],
[0.5, -0.5]
],
attributes: {
color: [
[1, 0, 0, 1],
[1, 0, 0, 1],
[1, 0, 0, 1],
[1, 0, 0, 1],
]
},
cells: [[0, 1, 2], [2, 0, 3]]
}]);
// ...上述这些代码比较简单,我就不过多解释了。
在画布上我们看到,绘制了一个红色的正方形,它是一个平面图形。

接下来,我们就在这个图形的基础上,将它拓展为3D的正立方体。
**要想把2维图形拓展为3维几何体,第一步就是要把顶点扩展到3维。**也就是把vec2扩展为vec3。
// vertex
attribute vec3 a_vertexPosition;
attribute vec4 color;
varying vec4 vColor;
void main() {
gl_PointSize = 1.0;
vColor = color;
gl_Position = vec4(a_vertexPosition, 1);
}当然仅仅修改Shader是不够的,因为数据是从JavaScript传递过来的,所以我们需要在JavaScript中计算立方体的顶点数据,然后再传递给Shader。
一个立方体有8个顶点,能组成6个面。在WebGL中需要用12个三角形来绘制它。
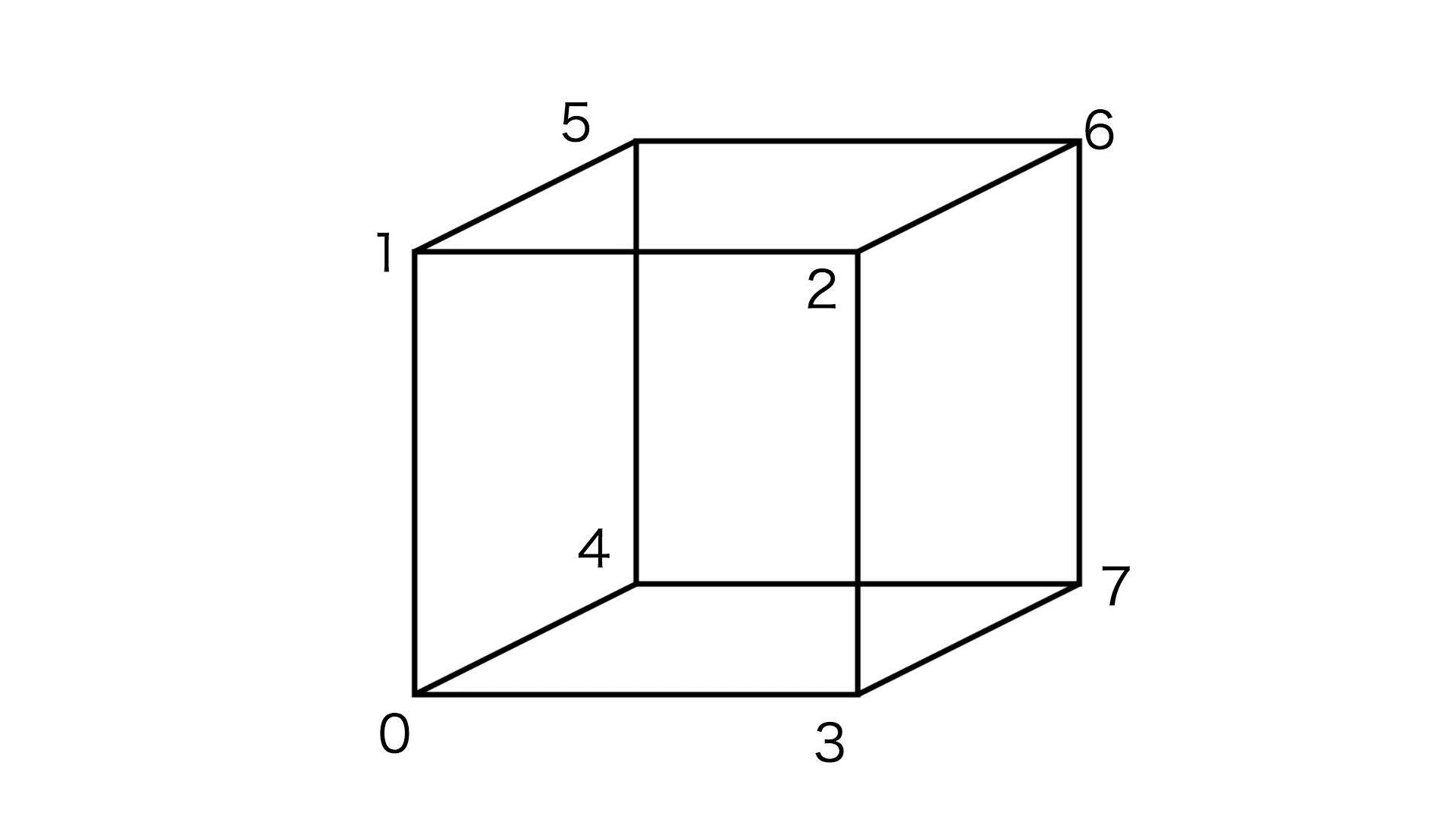
如果6个面的属性相同的话,我们可以复用8个顶点来绘制;
但如果属性不完全相同,比如每个面要绘制成不同的颜色,或者添加不同的纹理图片,就得把每个面的顶点分开。这样的话,就需要24个顶点来分别处理6个面。
为了方便使用,我们可以定义一个JavaScript函数,用来生成立方体6个面的24个顶点,以及12个三角形的索引,并且定义每个面的颜色。
/**
* 生成立方体6个面的24个顶点,12个三角形的索引,定义每个面的颜色信息
* @param size
* @param colors
* @returns {{cells: *[], color: *[], positions: *[]}}
*/
export function cube(size = 1.0, colors = [[1, 0, 0, 1]]) {
const h = 0.5 * size;
const vertices = [
[-h, -h, -h],
[-h, h, -h],
[h, h, -h],
[h, -h, -h],
[-h, -h, h],
[-h, h, h],
[h, h, h],
[h, -h, h]
];
const positions = [];
const color = [];
const cells = [];
let colorIdx = 0;
let cellsIdx = 0;
const colorLen = colors.length;
function quad(a, b, c, d) {
[a, b, c, d].forEach(item => {
positions.push(vertices[item]);
color.push(colors[colorIdx % colorLen]);
});
cells.push(
[0, 1, 2].map(i => i + cellsIdx),
[0, 2, 3].map(i => i + cellsIdx)
);
colorIdx ++;
cellsIdx += 4;
}
quad(1, 0, 3, 2); // 内
quad(4, 5, 6, 7); // 外
quad(2, 3, 7, 6); // 右
quad(5, 4, 0, 1); // 左
quad(3, 0, 4, 7); // 下
quad(6, 5, 1, 2); // 上
return {positions, color, cells};
}现在我们就可以通过调用cube这个函数,构建出立方体的顶点信息。
const geometry = cube(1.0, [
[1, 0, 0, 1], // 红
[0, 0.5, 0, 1], // 绿
[0, 0, 1, 1] // 蓝
]);通过这段代码,我们就能创建出一个棱长为1的立方体,并且六个面的颜色分别是"红、绿、蓝、红、绿、蓝"。
接下来我们就要把这个立方体的顶点信息传递给Shader。
在传递数据之前,我们需要先了解一个知识点,是关于绘制3D图形与2D图形存在的一点不同,那就是绘制3D图形时,必须要开启深度检测和启用深度缓冲区。
在WebGL中,我们可以通过**gl.enable(gl.DEPTH_TEST);** 这段代码来开启深度检测;在清空画布的时候,也要用**gl.clear(gl.COLOR_BUFFER_BIT | gl.DEPTH_BUFFER_BIT);**这段代码来同时清空颜色缓冲区和深度缓冲区。
启动和清空深度检测和深度缓冲区这两个步骤,非常重要。但是一般情况下,我们几乎不会用原生的方式来编写代码,所以了解一下即可。为了方便使用,在本文演示的例子中,我们还是直接使用gl-renderer这个库,它封装了深度检测,我们在使用时,在创建renderer的时候配置一个参数**depth: true**就可以了。
现在我们就把这个三维立方体用gl-renderer渲染出来。
// ...
renderer = new GlRenderer(glRef.value, {
depth: true // 开启深度检测
});
const program = renderer.compileSync(fragment, vertex);
renderer.useProgram(program);
renderer.setMeshData([{
positions: geometry.positions,
attributes: {
color: geometry.color
},
cells: geometry.cells
}]);
renderer.render();现在我们在画布上看到的是一个红色正方形,这是因为其他面被遮挡住了。

投影矩阵:变换WebGL坐标系
但是,等等,为什么我们看到的是红色的一面呢?按照我们所编写的代码,预期看到的应该是绿色的一面,也就是说我们预期Z轴是向外的,因为规范的直角坐标系是右手坐标系。所以按照现在的绘制结果,我们发现WebGL的坐标系其实是左手系的?
但一般来说,不管什么图形库或者图形框架,在绘图的时候,都会默认将坐标系从左手系转换为右手系,因为这更符合我们的使用习惯。所以这里,我们也去把WebGL的坐标系从左手系转换为右手系,简单来说,就是将Z轴坐标方向反转。关于坐标转换,可以通过齐次矩阵来完成。对坐标转换不熟悉的小伙伴,可以参考我之前的一篇关于仿射变换的文章。
将Z轴坐标方向反转,对应的齐次矩阵是这样的:
[
1, 0, 0, 0,
0, 1, 0, 0,
0, 0, -1, 0,
0, 0, 0, 1
]这种转换坐标的齐次矩阵,也被称为投影矩阵,ProjectionMatrix。
现在我们修改一下顶点着色器,把这个投影矩阵添加进去。
// vertex
attribute vec3 a_vertexPosition; // 1:把顶点从vec2扩展到vec3
attribute vec4 color; // 四维向量
varying vec4 vColor;
uniform mat4 projectionMatrix; // 2:投影矩阵-变换坐标系
void main() {
gl_PointSize = 1.0;
vColor = color;
gl_Position = projectionMatrix * vec4(a_vertexPosition, 1.0);
}现在我们就能看到画布上显示的是绿色的正方形了。

模型矩阵:让立方体旋转起来
现在我们只能看到立方体的一个面,因为Z轴是垂直于屏幕的,这样子从视觉上看好像和2维图形没什么区别,没法让人很直观地联想、感受到这是一个三维的几何体,为了将其他的面露出来,我们可以去旋转立方体。
要想旋转立方体,我们同样可以通过矩阵运算来实现。这个矩阵叫做模型矩阵,ModelMatrix,它定义了被绘制的物体变换。
把模型矩阵加入到顶点着色器中,将它与投影矩阵相乘,再乘上齐次坐标,就得到最终的顶点坐标了。
attribute vec3 a_vertexPosition; // 1:把顶点从vec2扩展到vec3
attribute vec4 color; // 四维向量
varying vec4 vColor;
uniform mat4 projectionMatrix; // 2:投影矩阵-变换坐标系
uniform mat4 modelMatrix; // 3:模型矩阵-使几何体旋转
void main() {
gl_PointSize = 1.0;
vColor = color;
gl_Position = projectionMatrix * modelMatrix * vec4(a_vertexPosition, 1.0);
}现在我们定义一个JavaScript函数,用立方体沿x、y、z轴的旋转来生成模型矩阵。
以x、y、z三个方向的旋转得到三个齐次矩阵,然后将它们相乘,就能得到最终的模型矩阵。
import { multiply } from 'ogl/src/math/functions/Mat4Func.js';
// ...
export function fromRotation(rotationX, rotationY, rotationZ) {
let c = Math.cos(rotationX);
let s = Math.sin(rotationX);
const rx = [
1, 0, 0, 0, // 绕X轴旋转
0, c, s, 0,
0, -s, c, 0,
0, 0, 0, 1
];
c = Math.cos(rotationY);
s = Math.sin(rotationY);
const ry = [
c, 0, s, 0,
0, 1, 0, 0, // 绕Y轴旋转
-s, 0, c, 0,
0, 0, 0, 1
];
c = Math.cos(rotationZ);
s = Math.sin(rotationZ);
const rz = [
c, s, 0, 0,
-s, c, 0, 0,
0, 0, 1, 0, // 绕Z轴旋转
0, 0, 0, 1
];
const ret = [];
multiply(ret, rx, ry);
multiply(ret, ret, rz);
return ret;
}我们把模型矩阵传给顶点着色器,不断更新三个旋转角度,就能实现立方体旋转的效果。
// ...
let rotationX = 0;
let rotationY = 0;
let rotationZ = 0;
function update() {
rotationX += 0.003;
rotationY += 0.005;
rotationZ += 0.007;
renderer.uniforms.modelMatrix = fromRotation(rotationX, rotationY, rotationZ);
requestAnimationFrame(update);
}
update();
// ...现在我们就能在旋转中看到立方体的其他几个面了,能更直观地感受到这是一个三维物体。

总结
至此,我们就实现了正立方体的绘制。在3D物体的绘制中,正立方体属于是比较简单的一类,屏幕前的小伙伴们都可以来动手尝试下,感兴趣的小伙伴,还可以尝试去实现圆柱体、正四面体等等这些几何体的绘制。
文章转载自: beckyye