栈和队列（四）-----双端队列

目录

双端队列

[力扣155 ---包含min函数的栈](#力扣155 ---包含min函数的栈)

题目

思路

代码

题目：滑动窗口最大值问题

题目

解题思路

---

双端队列

（Double-ended Queue，简称 deque）是一种具有队列和栈特性的数据结构。它允许在两端进行元素的添加和移除操作。具体来说，双端队列支持以下几种操作：

1. 在前端添加元素 （称为 appendleft 或 pushleft）：在队列的前端添加一个新元素，使得这个新元素成为队列的第一个元素。
2. 在前端移除元素 （称为 popleft）：移除队列的第一个元素，并返回它。
3. 在后端添加元素 （称为 append 或 push）：在队列的后端添加一个新元素，使得这个新元素成为队列的最后一个元素。
4. 在后端移除元素 （称为 pop）：移除队列的最后一个元素，并返回它。

双端队列的这些特性使得它在某些情况下比普通的队列或栈更加灵活。例如，它可以用于实现一个窗口，其中元素可以从两端进出，而不仅仅是一端。

在编程语言中，如 Python，双端队列通常由内置的 collections.deque 类提供。以下是 Python 中使用 deque 的一个简单示例：

from collections import deque

# 创建一个空的双端队列
dq = deque()

# 在后端添加元素
dq.append(1)
dq.append(2)

# 在前端添加元素
dq.appendleft(0)

# 从后端移除元素
last = dq.pop()

# 从前端移除元素
first = dq.popleft()

print(dq)  # 输出: deque([1], maxlen=None)

在这个示例中，我们首先创建了一个空的双端队列 dq，然后分别在两端添加了元素，并从两端移除了元素。最后，打印了队列中的剩余元素。

力扣155 ---包含min函数的栈

题目

设计一个支持 push ，pop ，top 操作，并能在常数时间内检索到最小元素的栈。

实现 MinStack 类:

• MinStack() 初始化堆栈对象。
• void push(int val) 将元素val推入堆栈。
• void pop() 删除堆栈顶部的元素。
• int top() 获取堆栈顶部的元素。
• int getMin() 获取堆栈中的最小元素。

示例 1:

输入：
["MinStack","push","push","push","getMin","pop","top","getMin"]
[[],[-2],[0],[-3],[],[],[],[]]

输出：
[null,null,null,null,-3,null,0,-2]

解释：
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.getMin();   --> 返回 -3.
minStack.pop();
minStack.top();      --> 返回 0.
minStack.getMin();   --> 返回 -2.

提示：

• -231 <= val <= 231 - 1
• pop、top 和 getMin 操作总是在 非空栈 上调用
• push, pop, top, and getMin最多被调用 3 * 104 次

思路

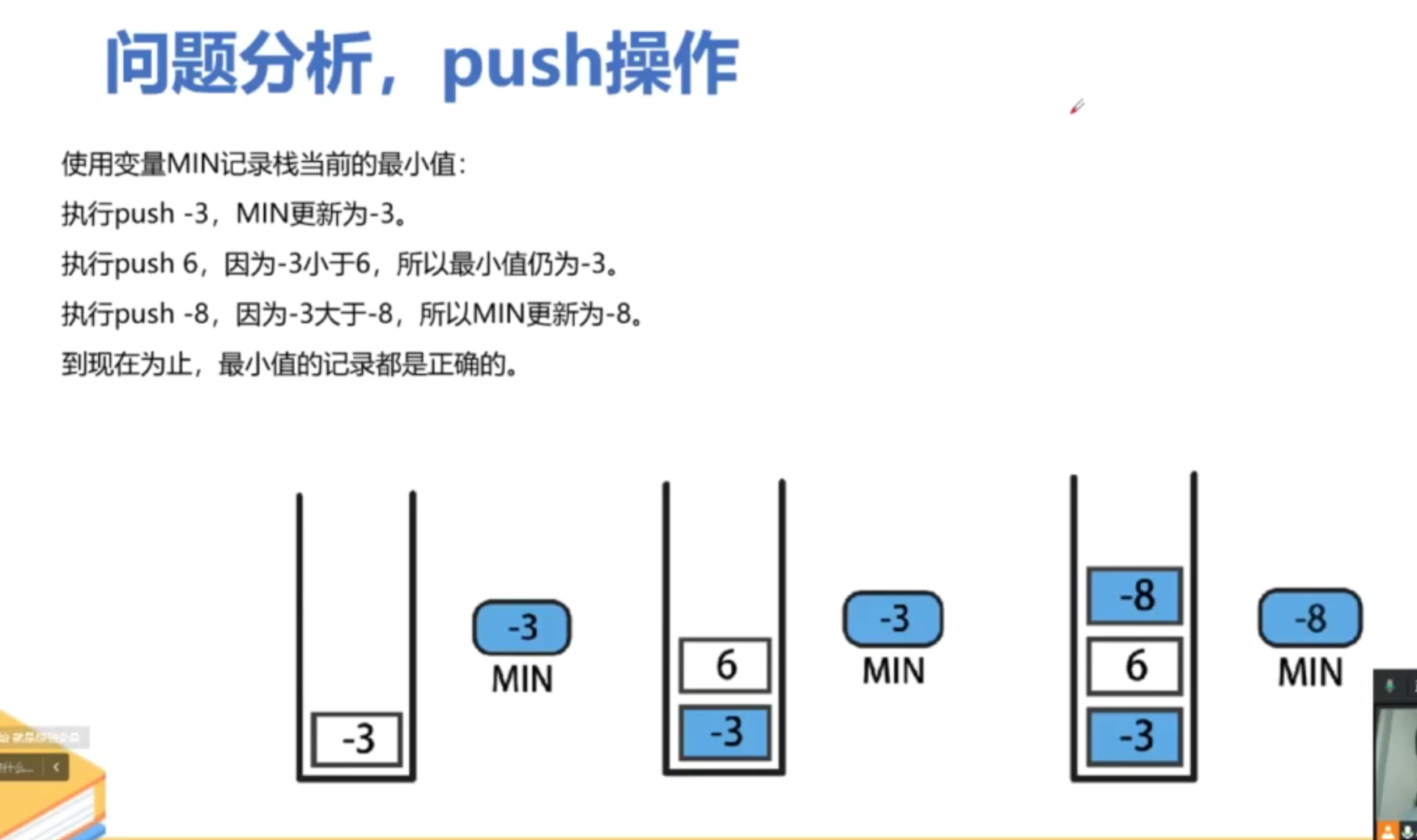
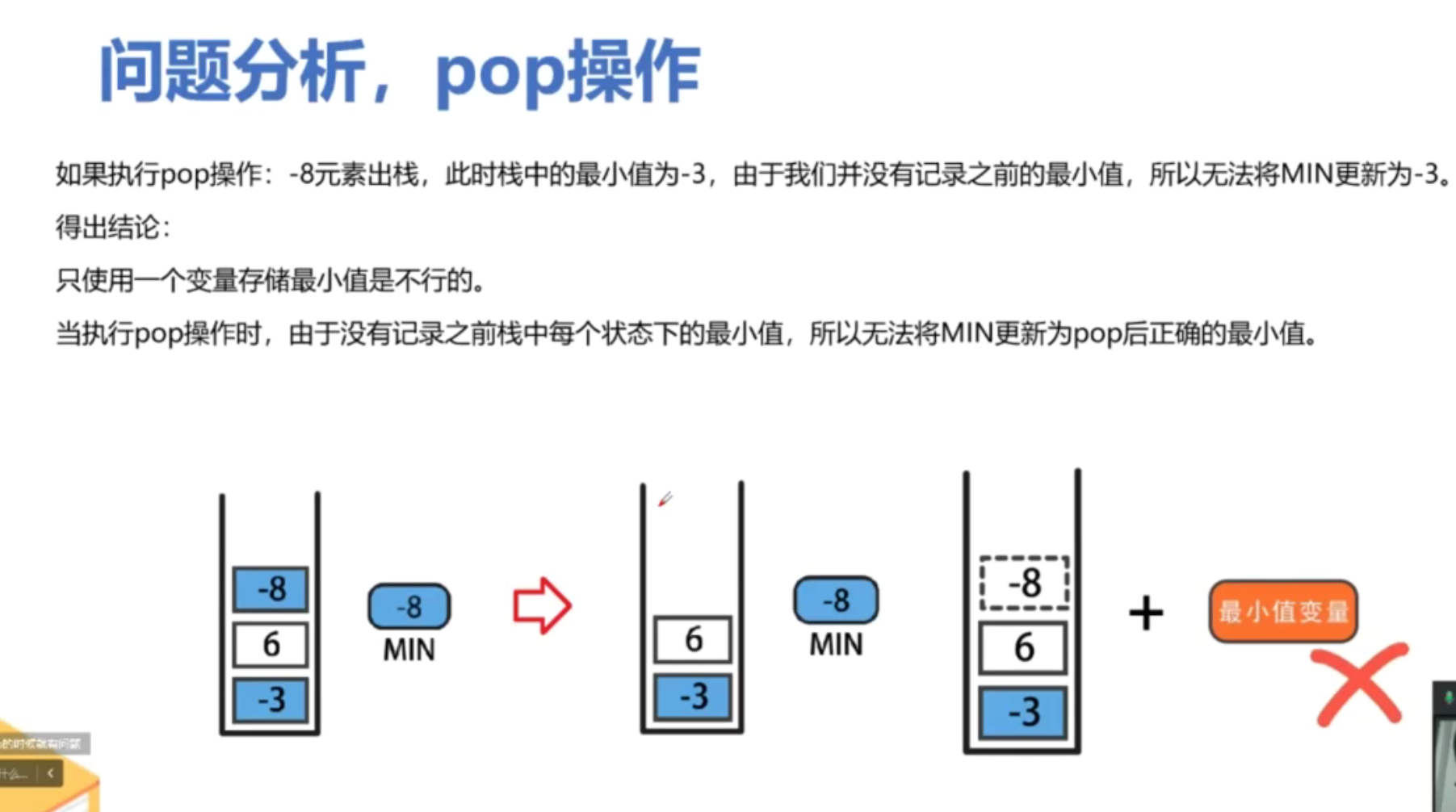
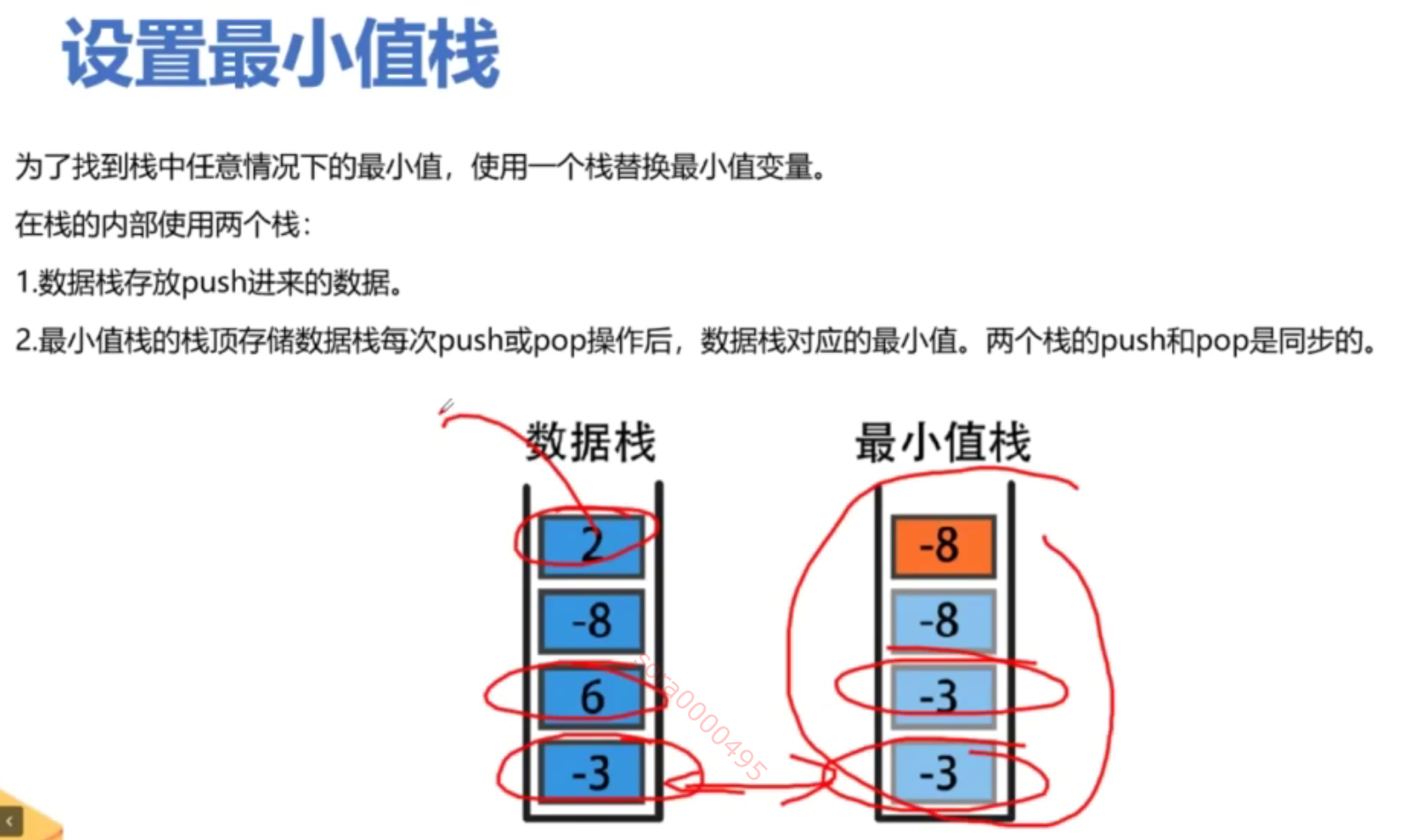
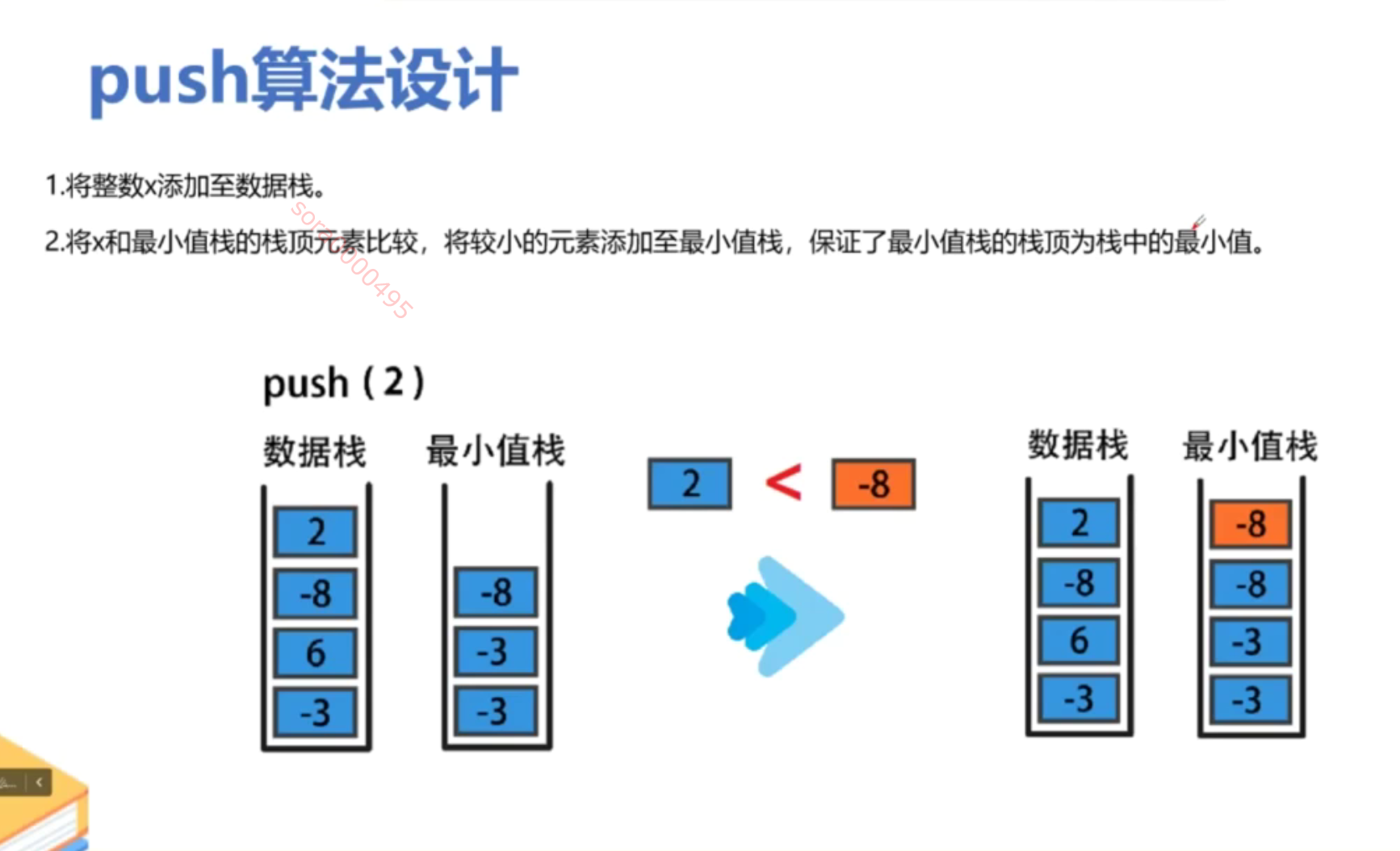
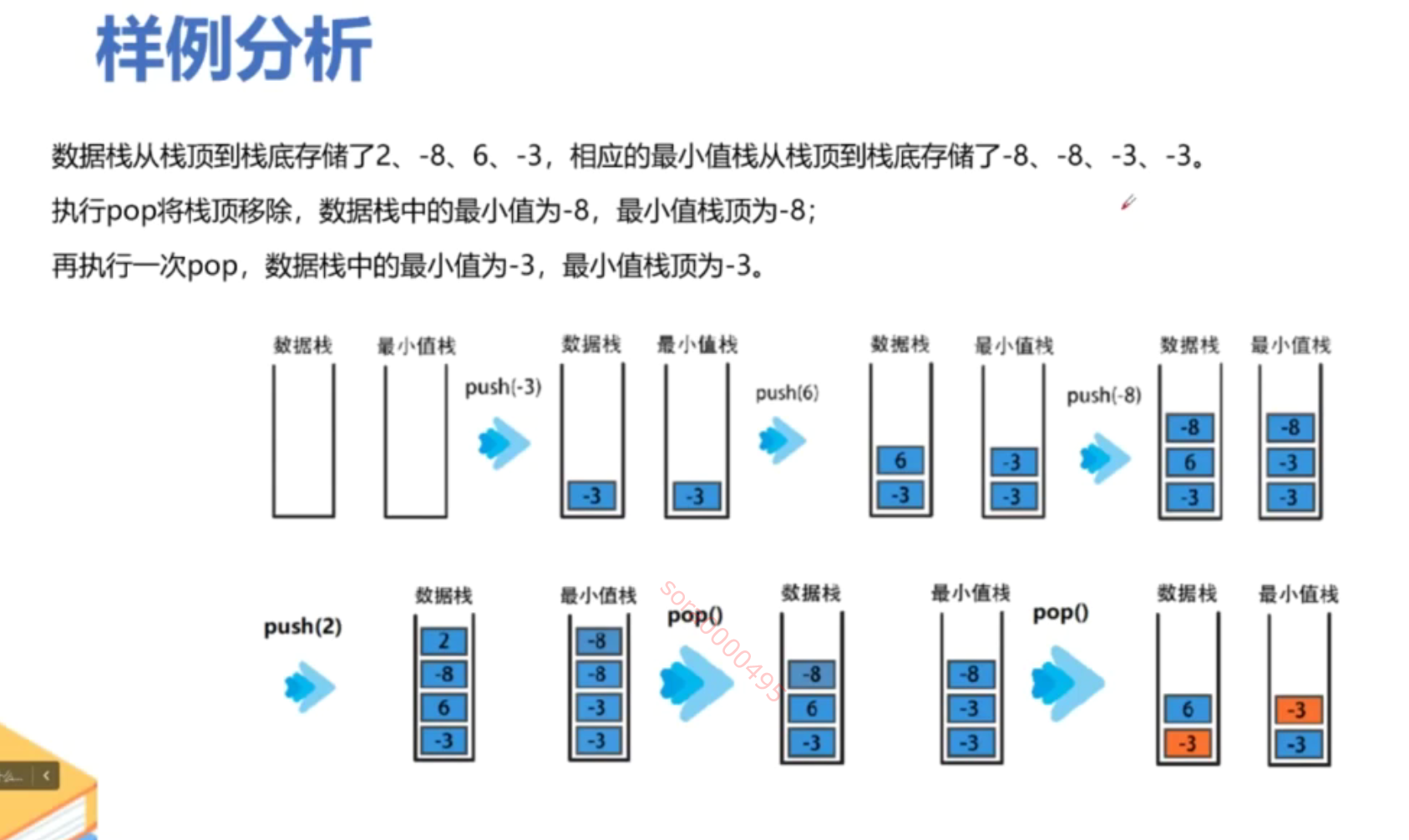
代码

class MinStack:
    def __init__(self):
        self.stack = []
        self.min_stack = [math.inf]

    def push(self, x: int) -> None:
        self.stack.append(x)
        self.min_stack.append(min(x, self.min_stack[-1]))

    def pop(self) -> None:
        self.stack.pop()
        self.min_stack.pop()

    def top(self) -> int:
        return self.stack[-1]

    def getMin(self) -> int:
        return self.min_stack[-1]

题目：滑动窗口最大值问题

题目

题目描述： 给定一个整数数组 nums 和一个滑动窗口的大小 k，请找出所有滑动窗口位置的最大值。

示例： 输入: nums = [1,3,-1,-3,5,3,6,7], 和 k = 3 输出: [3,3,5,5,6,7]

解释:

• 窗口位置 1: max = 3
• 窗口位置 2: max = 3
• 窗口位置 3: max = 5
• 以此类推...

要求：

• 你不能使用额外的数组来存储这些最大值，但可以使用一个队列来存储窗口中的元素的索引。

解题思路：

1. 使用双端队列（deque）来维护窗口中的元素索引。
2. 队列的前端始终是窗口中当前的最大值的索引。
3. 当队列不为空且窗口滑动使得队首元素索引小于窗口起始位置时，移除队首元素。
4. 当添加新元素到队列时，如果队列不为空且新元素大于队尾元素对应的值，则移除队尾元素，直到新元素小于或等于队尾元素对应的值或队列为空。
5. 每次窗口滑动后，将当前窗口的最大值（即队首元素对应的值）添加到结果数组中。

注意：

• 考虑使用单调队列来优化这个过程，单调队列可以保证队列的前端始终是当前窗口的最大值

解题思路

为了解决这个问题，我们可以使用一个队列（更具体地说，是双端队列 deque）来维护窗口中的元素索引。队列的前端始终是当前窗口中的最大值的索引。

步骤：

1. 初始化 ：创建一个双端队列 deque。
2. 填充窗口：从数组的开始，逐个将元素的索引添加到队列中。
3. 维护队列 ：
   • 每次添加新元素到队列时，检查队尾元素的索引对应的值是否小于新元素。如果是，移除队尾元素，直到新元素小于或等于队尾元素对应的值或队列为空。
   • 这确保了队列的前端始终是当前窗口的最大值的索引。
4. 滑动窗口 ：每次移动窗口时（即每次向右移动一个元素），检查队首元素的索引是否小于窗口的起始位置（即当前窗口的索引减去 k）。如果是，移除队首元素。
5. 输出最大值：每次移动窗口后，队首元素的索引对应的值就是当前窗口的最大值，将其添加到结果数组中。

from collections import deque

def maxSlidingWindow(nums, k):
    if not nums or k == 0:
        return []
    
    n = len(nums)
    max_queue = deque()
    result = []
    
    for i in range(n):
        # 维护队列，确保队首元素是当前窗口的最大值
        while max_queue and nums[max_queue[-1]] < nums[i]:
            max_queue.pop()
        max_queue.append(i)
        
        # 滑动窗口，移除不在窗口内的元素
        if max_queue and max_queue[0] <= i - k:
            max_queue.popleft()
        
        # 当窗口移动后，队首元素对应的值是当前窗口的最大值
        if i >= k - 1:
            result.append(nums[max_queue[0]])
    
    return result

# 示例
nums = [1,3,-1,-3,5,3,6,7]
k = 3
print(maxSlidingWindow(nums, k))  # 输出: [3,3,5,5,6,7]