
智能优化算法是一类基于自然界中生物、物理或社会现象的优化技术。这些算法通过模拟自然界中的一些智能行为,如遗传学、蚁群觅食、粒子群体运动等,来解决复杂的优化问题。智能优化算法广泛应用于各种工程和科学领域,因其具有全局搜索能力、鲁棒性强以及易于实现等优点。
灰狼优化算法(GWO)

灰狼优化算法(Grey Wolf Optimizer, GWO)是一种新兴的智能优化算法,灵感来源于灰狼的捕猎行为。该算法由Seyedali Mirjalili等人在2014年提出,模拟了灰狼的社会层次结构和合作狩猎的策略。
GWO算法自2014年提出以来,受到了广泛关注和研究。它不仅在学术界被广泛研究和引用,而且在工程优化、机器学习、图像处理等多个领域得到了成功应用。GWO最初只是作者在研究其他优化算法时的灵感,但最终却发展成为一个独立且强大的优化工具。
灰狼被认为是顶级捕食者,位于食物链的顶端。灰狼喜欢群居,每群平均有5至12只灰狼。如附图所示,群体中的所有个体都具有非常严格的社会支配等级。
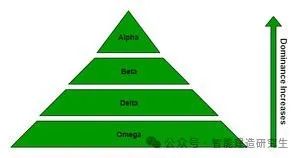
图2 灰狼的社会等级*
Alpha (α) 狼被视为狼群中的主导狼,狼群成员必须服从它的命令。
Beta (β) 是从属狼,帮助 Alpha 做出决策,被视为成为 Alpha 的最佳候选人。
Delta(δ)狼必须服从 Alpha 和 Beta,但它们主宰 Omega。δ 狼有不同的类别,如侦察兵、哨兵、长老、猎人、看守者等。
Omega (ω) 狼被视为狼群中的替罪羊,是狼群中最不重要的个体,只能在最后才被允许进食。
灰狼狩猎的主要阶段:
-
追踪、追逐并接近猎物。
-
追逐、包围、骚扰猎物,直到其停止移动。
-
向猎物发起攻击。
通过数学建模来设计灰狼的社会等级和狩猎行为,以设计 GWO。
数学模型与算法
社会等级
-
最适合的解决方案是Alpha狼(α)
-
第二最佳解决方案是 Beta 狼(β)
-
第三最佳解决方案是 Delta 狼(δ)
-
其余候选解决方案为 Omega 狼(ω)
数学模型
灰狼优化算法的数学模型描述了某个目标函的优化方法(寻找最优值,即猎物)
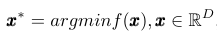
(1)需要优化的函数
其中是维向量。首先,随机生成个解
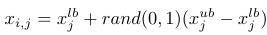
(2)初始化解决方案
其中,对应于特定维度分量,从和向量中返回随机值,这些向量是所有的下限和上限。根据狼的等级制度,三个最佳(达到最低值)解决方案α、β和δ(通常为)分别映射到 α、β 和 δ 狼。我们假设领导者对猎物的位置有最丰富的经验,因此他们会指挥其他狼。猎物位置(由领导者确定)与狼群其他成员之间的距离计算为
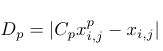
(3)距离计算
其中是每个领导者的位置分量(与猎物位置大致相同),是每个解决方案的分量,是 来自 [0, 2] 的特殊随机参数。此参数指定"随机性"------在猎物邻域中搜索。在计算与领导者相关的三个距离后,我们应该计算他们的新位置,如下所示(这里的与分量不同,它只是另一个变量)
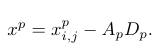
(4)领导职位
最后一个等式意味着我们通过距离值乘以某个随机因子来接近猎物。值和是算法的关键参数。第一个等式增加了特殊的随机性,即如果(探索阶段),它允许狼通过偏离
来寻找更好的猎物。否则,如果,那么狼的新位置可以位于先前位置和猎物位置之间的任何区域。这意味着狼开始攻击猎物。在迭代过程中,该值通过以下公式进行更改
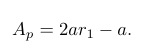
(5)计算
这里是从 2(初始值)下降到 0 的递减(通常是线性的)因子
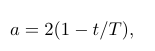
(6)递减因子计算
其中是当前迭代次数,是预先定义的总迭代次数,是 中的随机值。
参数(也是 中的随机值*)
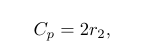
(7)C_p计算
可以看作是狼在野外接近猎物时遇到的障碍物的影响。在自然界中,这些障碍物通常表现为狼狩猎路线上的障碍物,有效地阻碍了它们迅速轻松地接近猎物的能力。换句话说,它可能会随机为猎物分配一个难度或距离等级,使狼要么更难接近猎物,要么更难接近猎物,或者相反,更容易接近猎物。迫使狼进行探索而不是开发,并有助于避免局部最小值。
生成值后,可以计算出狼的新位置,作为的平均值
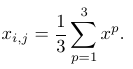
(8)计算新解
所描述的过程如下所示。
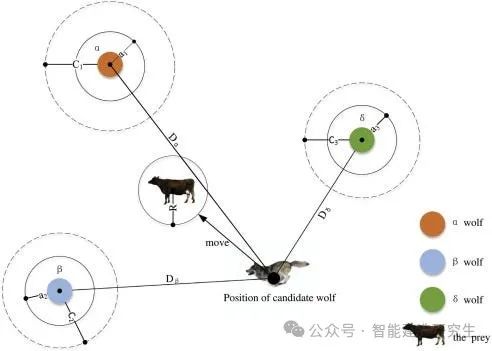
img
算法详见:https://doi.org/10.1016/j.knosys.2019.01.018IF: 7.2 Q1
GWO 算法的伪代码
1. 初始化解的数量 N、总迭代次数T和边界向量 x^{ub}, x^{lb};
2. 使用公式 (2) 随机生成 N 个解;
3. 确定三个最佳解 (领导者) X^p,p=1..3;
3. 对于 t=1..N(迭代循环):
4. 通过 (6) 计算值 a;
5. 对于每个第 i 个解:
6. 对于每个第 j 个维度:
7. 使用 (5) 和 (7) 计算 A_p 和 C_p;
8. 通过 (3) 计算三个距离 D_p;
9. 通过 (4) 计算三个 x^p;
10. 通过 (8) 生成新的解分量 x^{new}_{i,j};
11. 如果 x^{new}_{i,j} 位于 x^{ub} 或 x^{lb} 之外,
则将相应的 x^{ub} 或 x^{lb} 分配给 x^{new}_{i,j};
12. 如果 f(x^{new}_i)>f(x_i),则丢弃 x^{new}_i,保留前一个
x_i,即 x^{new}_i = x_i (与 x_i(t+1) = x_i(t) 相同);
13. 更新三个最佳解(领导者)X^p,p=1..3。详情参见:https://www.sciencedirect.com/science/article/pii/S0965997813001853
应用领域和场景
灰狼优化算法因其简单、高效和全局搜索能力强,广泛应用于:
-
多层感知器的训练算法
-
训练 q-高斯径向基函数链接网络
-
经济调度问题
-
特征子集选择
-
电力系统电网
-
进化种群动态
-
优化关键值
网址:https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0287405
参考资料:https://medium.com/@deneb.acyg/grey-wolf-optimizer-in-c-part-1-intuition-232be414f4ad
https://journals.plos.org/plosone/article?id=10.1371/journal.pone.0287405
基于Python的可视化算法实例
下面是一个基于Python实现的GWO算法实例,并通过可视化展示其优化过程:
import numpy as np # 导入NumPy库,用于数值计算
import matplotlib.pyplot as plt # 导入matplotlib的pyplot模块,用于绘图
# 定义一个灰狼优化器类
class GreyWolfOptimizer:
# 初始化方法
def __init__(self, objective_function, dimension, lower_bound, upper_bound, population_size, iterations):
self.objective_function = objective_function # 目标函数
self.dimension = dimension # 问题的维度
self.lower_bound = np.array(lower_bound) # 参数的下界
self.upper_bound = np.array(upper_bound) # 参数的上界
self.population_size = population_size # 群体大小
self.iterations = iterations # 迭代次数
# 初始化种群
self.population = np.random.rand(population_size, dimension) * (self.upper_bound - self.lower_bound) + self.lower_bound
self.alpha = self.population[0] # 初始化alpha狼
self.beta = self.population[1] # 初始化beta狼
self.delta = self.population[2] # 初始化delta狼
# 优化方法
def optimize(self):
for _ in range(self.iterations): # 对每一代进行迭代
for i in range(self.population_size): # 遍历种群中的每一个个体
# 计算每个维度的系数A, C和距离D
A = 2 * np.random.rand(self.dimension) - 1
C = 2 * np.random.rand()
D_alpha = np.abs(C * self.alpha - self.population[i])
X1 = self.alpha - A * D_alpha
A = 2 * np.random.rand(self.dimension) - 1
C = 2 * np.random.rand()
D_beta = np.abs(C * self.beta - self.population[i])
X2 = self.beta - A * D_beta
A = 2 * np.random.rand(self.dimension) - 1
C = 2 * np.random.rand()
D_delta = np.abs(C * self.delta - self.population[i])
X3 = self.delta - A * D_delta
self.population[i] = (X1 + X2 + X3) / 3 # 更新个体位置
# 计算种群的适应度
fitness = np.array([self.objective_function(ind) for ind in self.population])
# 根据适应度排序并更新alpha, beta, delta
best_indexes = np.argsort(fitness)[:3]
self.alpha, self.beta, self.delta = self.population[best_indexes]
# 定义电网优化的目标函数
def power_system_optimization(x):
return np.sum(x**2) # 返回所有参数的平方和
# 初始化优化器参数
dimension = 5
lower_bound = [0]*dimension
upper_bound = [100]*dimension
population_size = 30
iterations = 50
# 创建灰狼优化器实例
gwo = GreyWolfOptimizer(power_system_optimization, dimension, lower_bound, upper_bound, population_size, iterations)
gwo.optimize() # 进行优化
# 可视化优化过程中Alpha, Beta, Delta的变化
plt.plot(gwo.alpha, label='Alpha')
plt.plot(gwo.beta, label='Beta')
plt.plot(gwo.delta, label='Delta')
plt.xlabel('Iteration')
plt.ylabel('Value')
plt.legend()
plt.title('GWO Optimization Process')
plt.show() # 显示图表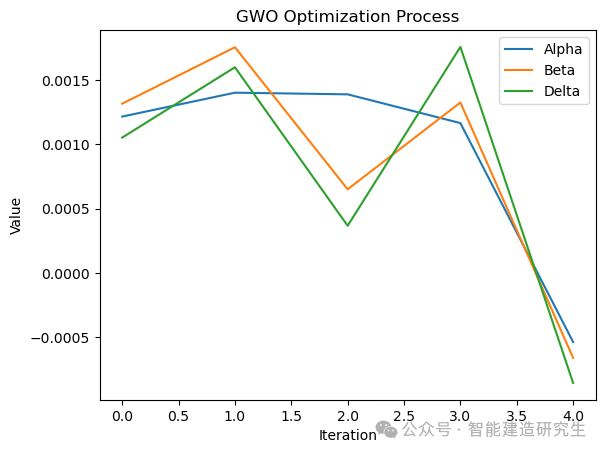
在上面的示例中,GWO算法被用于优化一个简化的电力系统模型,其中目标函数定义为所有变量的平方和,代表了一个假设的优化目标。代码初始化一个包含随机值的种群,然后通过迭代过程不断更新种群中个体的位置,以寻找最小化目标函数的解。这个过程中,算法更新了三个最优解,即 Alpha、Beta 和 Delta,它们代表了种群中的最优个体。
以上内容总结自网络,如有帮助欢迎关注与转发,我们下次再见!