嵌入式面试准备

两数之和

暴力枚举

cpp 复制代码

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int n = nums.size();
        for(int i=0; i<n-1; i++){
            for(int j=i+1; j<n; j++){
                if(nums[i] + nums[j] == target){
                    return {i,j};
                }
            }
        }
        return {0,0};
    }
};

哈希表

暴力枚举的时间复杂度高的原因是寻找target-x的时间复杂度过高。

cpp 复制代码

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> map1; //<num, index>
        int n = nums.size();
        for(int i=0; i<n; i++){
            if(map1.count(target-nums[i])){
                return {map1[target-nums[i]], i};
            }else{
                map1[nums[i]] = i;
            }
        }
        return {0,0};
    }
};

三数之和

cpp 复制代码

class Solution {
public:
    vector<vector<int>> threeSum(vector<int>& nums) {
        vector<vector<int>> res;
        sort(nums.begin(),nums.end());
        int n = nums.size();
        for(int i=0; i<n-2; i++){
            if(i!=0 && nums[i]==nums[i-1]){
                continue;
            }
            int j = i+1;
            int k = nums.size()-1;
            while(j < k){
                if(nums[i]+nums[j]+nums[k] == 0){
                    res.push_back({nums[i],nums[j],nums[k]});
                    do{
                        j++;
                        k--;
                    }while(j<k && nums[j]==nums[j-1] && nums[k]==nums[k+1]);
                    
                }else if(nums[i]+nums[j]+nums[k] < 0){
                    j++;
                }else{
                    k--;
                }
            }
            
        }
        return res;
    }
};

二叉树的最近公共祖先

存储父节点

可以用哈希表存储所有节点的父节点，然后从p节点依次向上跳，将经过的地方标记为true。q节点向上跳，遇到的第一个为true的节点，就是公共节点。

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode(int x) : val(x), left(NULL), right(NULL) {}
 * };
 */
class Solution {
public:
    unordered_map<int, TreeNode*> father;
    unordered_map<int, bool> visited;

    void createFather(TreeNode* root){
        if(root->left){
            father[root->left->val] = root;
            createFather(root->left);
        }
        if(root->right){
            father[root->right->val] = root;
            createFather(root->right);
        }
    }

    TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
        father[root->val] = nullptr;
        createFather(root);

        while(p){
            visited[p->val] = true;
            p = father[p->val];
        }

        while(q){
            if(visited[q->val]){
                return q;
            }
            q = father[q->val];
        }

        return nullptr;
    }
};

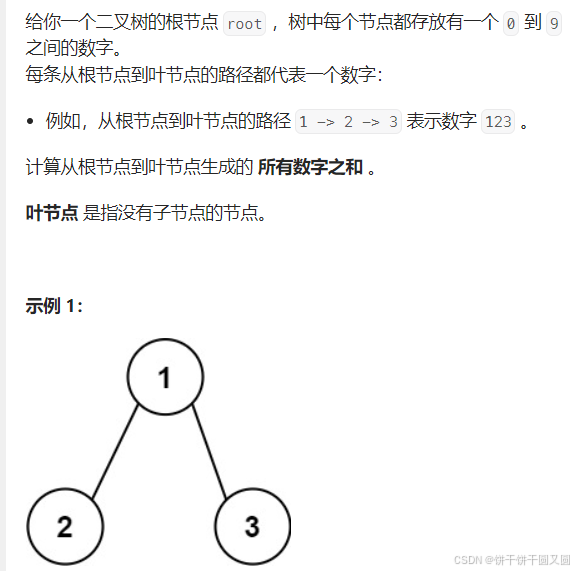
求根节点到叶节点数字之和

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    void dfs(TreeNode* root, vector<int>& nums, int sum){
        if(root->left == nullptr && root->right == nullptr){
            nums.push_back(sum*10 + root->val);
            return;
        }
        sum = (sum * 10) + root->val;
        if(root->left){
            dfs(root->left, nums, sum);
        }
        if(root->right){
            dfs(root->right, nums, sum);
        }   
    }
    int sumNumbers(TreeNode* root) {
        vector<int> nums;
        dfs(root, nums, 0);
        int sum = 0;
        for(int num: nums){
            sum += num;
        }
        return sum;
    }
};

二叉树展开为链表

cpp 复制代码

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left),
 * right(right) {}
 * };
 */
class Solution {
public:
    void inorder(TreeNode* root, vector<TreeNode*>& nums) {
        if (root != nullptr) {
            nums.push_back(root);
            inorder(root->left, nums);
            inorder(root->right, nums);
        }
    }
    void flatten(TreeNode* root) {
        if(root == nullptr){
            return;
        }
        vector<TreeNode*> nums;
        inorder(root, nums);

        TreeNode* p = root;
        p->left = nullptr;
        for (int i = 1; i < nums.size(); i++) {
            nums[i]->left = nullptr;
            nums[i]->right = nullptr;
            p->right = nums[i];
            p = nums[i];
        }
    }
};

爬楼梯

cpp 复制代码

class Solution {
public:
    int climbStairs(int n) {
        if(n <= 2){
            return n;
        }
        int p = 1, q = 2;
        for(int i=3; i<=n; i++){
            int sum = p+q;
            p = q;
            q = sum;
        }
        return q;
    }
};

打家劫舍

动态规划

如果只有一间房屋，则偷窃该房屋获得最高金额。

如果有两件，选择其中最高的一间，获得最高金额。

如果房间数量大于2，对于第k间房屋：

偷窃第k间房，偷窃总金额为前k-1的最高总金额加上第k间房。
不偷窃第k间房，偷窃总金额为前k-1的最高总金额。

cpp 复制代码

class Solution {
public:
    int rob(vector<int>& nums) {
        int n = nums.size();
        if(n == 1){
            return nums[0];
        }
        if(n == 2){
            return max(nums[0], nums[1]);
        }
        
        vector<int> dp(n, 0); //dp[i]偷到第i个房间的最高金额
        dp[0] = nums[0];
        dp[1] = max(nums[0], nums[1]);

        for(int i=2; i<n; i++){
            dp[i] = max(dp[i-1], dp[i-2] + nums[i]);
        }
        return dp[n-1];

    }
};

单词拆分

定义dp[i]表示0,...,i-1是否能被空格拆分成若干字典中出现的单词。

cpp 复制代码

class Solution {
public:
    bool wordBreak(string s, vector<string>& wordDict) {
        unordered_set<string> set1;
        for(string word : wordDict){
            set1.insert(word);
        }

        int n = s.size();
        vector<int> dp(n+1);
        dp[0] = true;
        for(int i=1; i<=n; i++){
            for(int j=0; j<i; j++){
                if(dp[j] && set1.find(s.substr(j, i-j)) != set1.end()){
                    dp[i] = true;
                    break;
                }
            }
        }
        return dp[n];
    }
};

最长递增子序列

cpp 复制代码

class Solution {
public:
    int lengthOfLIS(vector<int>& nums) {
        int n = nums.size();
        vector<int> dp(n, 0); //dp[i]为0,...,i最长序列，且nums[i]被选取
        dp[0] = 1;
        for(int i=1; i<=n-1; i++){
            dp[i] = 1;
            for(int j=0; j<i; j++){
                if(nums[i] > nums[j]){
                    dp[i] = max(dp[i], dp[j]+1);
                }else if(nums[i] == nums[j]){
                    dp[i] = max(dp[i], dp[j]);
                }
            }
        }
        return *max_element(dp.begin(), dp.end());
    }
};

最小路径和

cpp 复制代码

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int m = grid.size(), n = grid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));
        dp[0][0] = grid[0][0];
        for(int i=0; i<m; i++){
            for(int j=0; j<n; j++){
                if(i == 0 && j == 0){
                    continue;
                }
                if(i == 0){
                    dp[i][j] = dp[i][j-1] + grid[i][j];
                }else if(j == 0){
                    dp[i][j] = dp[i-1][j] + grid[i][j];
                }else{
                    dp[i][j] = min(dp[i][j-1], dp[i-1][j]) + grid[i][j];
                }
            }
        }

        return dp[m-1][n-1];
    }
};

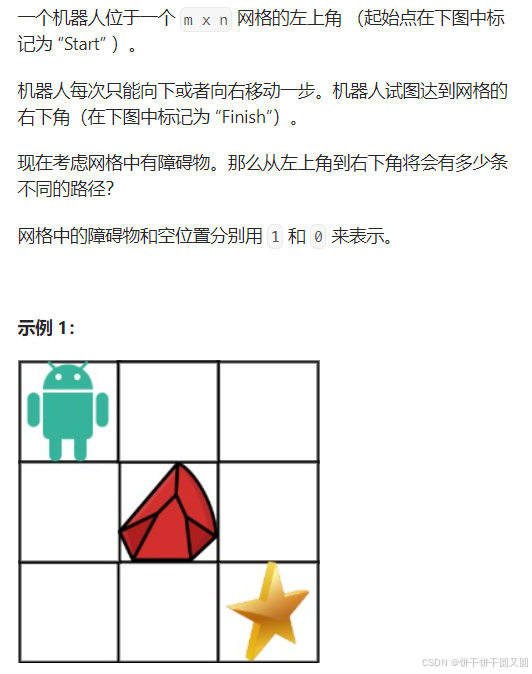
不同路径二

cpp 复制代码

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int m = obstacleGrid.size(), n = obstacleGrid[0].size();
        vector<vector<int>> dp(m, vector<int>(n, 0));
        if(obstacleGrid[0][0] == 1){
            return 0;
        }
        dp[0][0] = 1;
        for(int i=0; i<m; i++){
            for(int j=0; j<n; j++){
                if(i == 0 && j == 0){
                    continue;
                }
                if(obstacleGrid[i][j] == 1){
                    dp[i][j] = 0;
                }else{
                    if((i == 0 && dp[i][j-1] != 0) || (j == 0 && dp[i-1][j] != 0)){
                        dp[i][j] = 1;
                    }else if(i == 0 || j == 0){
                        dp[i][j] = 0;
                    }else{
                        if(dp[i-1][j] != 0){
                            dp[i][j] += dp[i-1][j];
                        }
                        if(dp[i][j-1] != 0){
                            dp[i][j] += dp[i][j-1];
                        }
                    }
                }
            }
        }
        return dp[m-1][n-1];
    }
};

编辑距离

给两个单词word1和word2，请返回将word1转换成word2所使用的最少操作数。

cpp 复制代码

class Solution {
public:
    int minDistance(string word1, string word2) {
        int m = word1.size(), n = word2.size();
        if(n * m == 0){
            return n+m;
        }

        vector<vector<int>> dp(m+1, vector<int>(n+1)); //dp[i][j] 以i-1替换成j-1的最小操作次数
        for(int i=0; i<=m; i++){
            dp[i][0] = i;  //删除i个变为空
        }
        for(int j=0; j<=n; j++){
            dp[0][j] = j; //增加j个变为word2
        }

        for(int i=1; i<=m; i++){
            for(int j=1; j<=n; j++){
                if(word1[i-1] == word2[j-1]){
                    dp[i][j] = dp[i-1][j-1];
                }else{
                    int del = dp[i-1][j] + 1;
                    int add = dp[i][j-1] + 1;
                    int rep = dp[i-1][j-1] + 1;
                    dp[i][j] = min(del, min(add, rep));
                }
            }
        }

        return dp[m][n];
    }
};