字节
最近,有不少大厂陆续开启校招。
当中就包括宣布今年有 4000+ 研发需求的国内大厂字节跳动。
但也是近期,不少同学发帖表示,投递字节,遭受了各种挂。
这位同学是山西大学(双一流)毕业生,据这位同学提供的截图,在8月1日投递了后端、测开和 C++ 几个岗位,在8月2日便显示流程终止。
这种情况显然连初筛都没过,不少同学猜测:字节开始挑学历了。
也有同学在评论区指出,可能是日常实习不缺人,根本没有 HC,这时候只能指望内推。

另外一位同学的经历更加离谱,在收到字节的笔试邀请函之后,结果笔试开始时间还没到,就收到了进入人才库的通知:

能够收到笔试邀请邮件,说明简历已经通过初筛,转头又收到感谢信,这看上去更多的是字节跳动的流程混乱问题。
不少同学表示经历相同,具体原因不得而知,只能猜测「笔试」和「简历评估」是两条线,挂简历不受已发笔试邀请的影响。
如果上面这两位同学经历还能理解,那么这位同学真的太冤了:

收到了笔试邀请(说明初筛过了),笔试也 AK 了,结果连面试机会都没有。
对此,你怎么看?
...
回归主题。
来一道和「外企」相关的算法原题。
题目描述
平台:LeetCode
题号:952
给定一个由不同正整数的组成的非空数组 nums,考虑下面的图:
- 有
nums.length个节点,按从nums[0]到nums[nums.length - 1]标记; - 只有当
nums[i]和nums[j]共用一个大于 的公因数时,nums[i]和nums[j]之间才有一条边。
返回图中最大连通组件的大小。
示例 1:

输入:nums = [4,6,15,35]
输出:4示例 2:

输入:nums = [20,50,9,63]
输出:2示例 3:
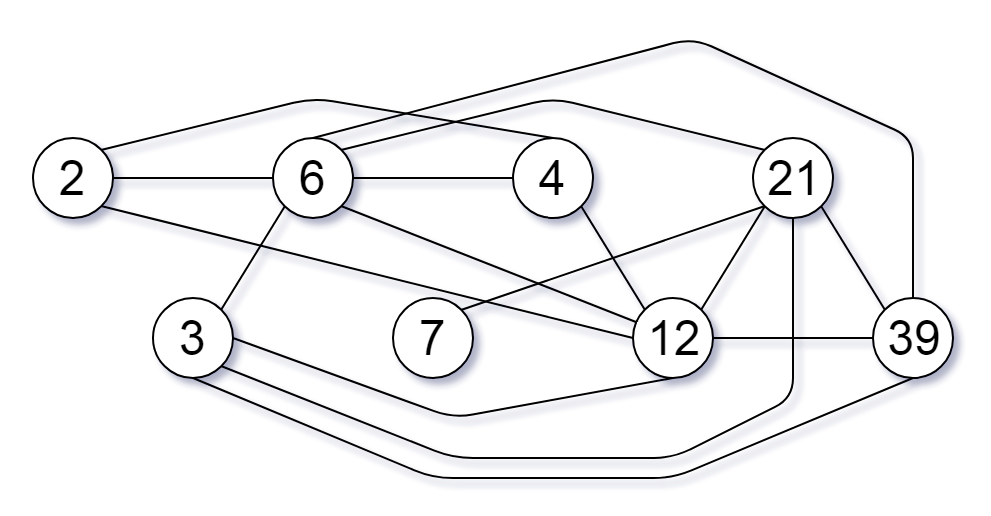
输入:nums = [2,3,6,7,4,12,21,39]
输出:8提示:
nums中所有值都 不同
枚举质因数 + 并查集
先考虑如何使用 nums 进行建图,nums 大小为 ,枚举所有点对并通过判断两数之间是否存在边的做法复杂度为 (其中 为 的最大值),无须考虑。
而不通过「枚举点 + 求公约数」的建图方式,可以对 进行质因数分解(复杂度为 ),假设其分解出来的质因数集合为 S,我们可以建立从 S_{k} 到 的映射关系,若 与 存在边,则 和 至少会被同一个质因数所映射。
维护连通块数量可以使用「并查集」来做,维护映射关系可以使用「哈希表」来做。
维护映射关系时,使用质因数为 key,下标值 为 value(我们使用下标 i 作为点编号,而不是使用 ,是利用 各不相同,从而将并查集数组大小从 收窄到 )。
同时在使用「并查集」维护连通块时,同步维护每个连通块大小 sz 以及当前最大的连通块大小 ans。
Java 代码:
class Solution {
static int N = 20010;
static int[] p = new int[N], sz = new int[N];
int ans = 1;
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
void union(int a, int b) {
if (find(a) == find(b)) return ;
sz[find(a)] += sz[find(b)];
p[find(b)] = p[find(a)];
ans = Math.max(ans, sz[find(a)]);
}
public int largestComponentSize(int[] nums) {
int n = nums.length;
Map<Integer, List<Integer>> map = new HashMap<>();
for (int i = 0; i < n; i++) {
int cur = nums[i];
for (int j = 2; j * j <= cur; j++) {
if (cur % j == 0) add(map, j, i);
while (cur % j == 0) cur /= j;
}
if (cur > 1) add(map, cur, i);
}
for (int i = 0; i <= n; i++) {
p[i] = i; sz[i] = 1;
}
for (int key : map.keySet()) {
List<Integer> list = map.get(key);
for (int i = 1; i < list.size(); i++) union(list.get(0), list.get(i));
}
return ans;
}
void add(Map<Integer, List<Integer>> map, int key, int val) {
List<Integer> list = map.getOrDefault(key, new ArrayList<>());
list.add(val);
map.put(key, list);
}
}C++ 代码:
class Solution {
public:
static const int N = 20010;
vector<int> p, sz;
int ans = 1;
Solution() : p(N), sz(N, 1) {
for (int i = 0; i < N; ++i) p[i] = i;
}
int find(int x) {
if (p[x] != x) p[x] = find(p[x]);
return p[x];
}
void unions(int a, int b) {
if (find(a) == find(b)) return ;
sz[find(a)] += sz[find(b)];
p[find(b)] = p[find(a)];
ans = max(ans, sz[find(a)]);
}
int largestComponentSize(vector<int>& nums) {
unordered_map<int, vector<int>> map;
for (int i = 0; i < nums.size(); i++) {
int cur = nums[i];
for (int j = 2; j * j <= cur; j++) {
if (cur % j == 0) add(map, j, i);
while (cur % j == 0) cur /= j;
}
if (cur > 1) add(map, cur, i);
}
for (auto& pair : map) {
for (int i = 1; i < pair.second.size(); i++) {
unions(pair.second[0], pair.second[i]);
}
}
return ans;
}
void add(unordered_map<int, vector<int>>& map, int key, int val) {
map[key].push_back(val);
}
};Python 代码:
class Solution:
def __init__(self):
self.p = [i for i in range(20010)]
self.sz = [1] * 20010
self.ans = 1
def find(self, x):
if self.p[x] != x:
self.p[x] = self.find(self.p[x])
return self.p[x]
def union(self, a, b):
if self.find(a) == self.find(b):
return
self.sz[self.find(a)] += self.sz[self.find(b)]
self.p[self.find(b)] = self.p[self.find(a)]
self.ans = max(self.ans, self.sz[self.find(a)])
def largestComponentSize(self, nums):
mapping = defaultdict(list)
for i, num in enumerate(nums):
for j in range(2, int(math.sqrt(num)) + 1):
if num % j == 0:
self.add(mapping, j, i)
while num % j == 0:
num //= j
if num > 1:
self.add(mapping, num, i)
for vals in mapping.values():
for i in range(1, len(vals)):
self.union(vals[0], vals[i])
return self.ans
def add(self, mapping, key, val):
mapping[key].append(val)TypeScript 代码:
const N = 20010
const p: number[] = new Array<number>(N), sz = new Array<number>(N)
let ans = 0
function find(x: number): number {
if (p[x] != x) p[x] = find(p[x])
return p[x]
}
function union(a: number, b: number): void {
if (find(a) == find(b)) return
sz[find(a)] += sz[find(b)]
p[find(b)] = p[find(a)]
ans = Math.max(ans, sz[find(a)])
}
function largestComponentSize(nums: number[]): number {
const n = nums.length
const map: Map<number, Array<number>> = new Map<number, Array<number>>()
for (let i = 0; i < n; i++) {
let cur = nums[i]
for (let j = 2; j * j <= cur; j++) {
if (cur % j == 0) add(map, j, i)
while (cur % j == 0) cur /= j
}
if (cur > 1) add(map, cur, i)
}
for (let i = 0; i < n; i++) {
p[i] = i; sz[i] = 1
}
ans = 1
for (const key of map.keys()) {
const list = map.get(key)
for (let i = 1; i < list.length; i++) union(list[0], list[i])
}
return ans
};
function add(map: Map<number, Array<number>>, key: number, val: number): void {
let list = map.get(key)
if (list == null) list = new Array<number>()
list.push(val)
map.set(key, list)
}- 时间复杂度:
- 空间复杂度:
最后
巨划算的 LeetCode 会员优惠通道目前仍可用 ~
使用福利优惠通道 leetcode.cn/premium/?promoChannel=acoier ,年度会员 有效期额外增加两个月 ,季度会员 有效期额外增加两周,更有超大额专属 🧧 和实物 🎁 福利每月发放。
我是宫水三叶,每天都会分享算法知识 ,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉