1. 题目
2. 解题思路
题目精简一下:
给你两个数组,从每个数组选取N个元素(需要保持相对顺序,比如从数组[4,8,2]选取两个元素,选取出来后必须保持顺序,比如选4和2,那么组成新数组这两个元素的顺序必须还是4在2前面),元素总长度不超过K,组成一个最大的数组。
核心思路如下:
从两个数组分别选取不同长度的子序列,进行merge后再进行比较。那么可以拆分为几个步骤:
1、从数组1选取N个元素,数组2选取K-N个元素,分别组成两个子序列
2、从两个数组组成对应的子序列,使用单调栈思想(遍历数组,如果当前数字比已选择的最后一个数字大,并且还可以替换元素,则删除已选的元素并选取当前更大的元素。),选出数组中最大的子序列,然后进行合并即可
所以可以知道,我们需要几个核心方法
- 从传入的数组中选取特定长度的最大子序列
- 合并子序列为一个完整数组
- 判断来比较两个数组(或者两个数组的剩余部分)哪个"更大"
3. 代码
3.1. 注意事项
1、首先来看下这段代码
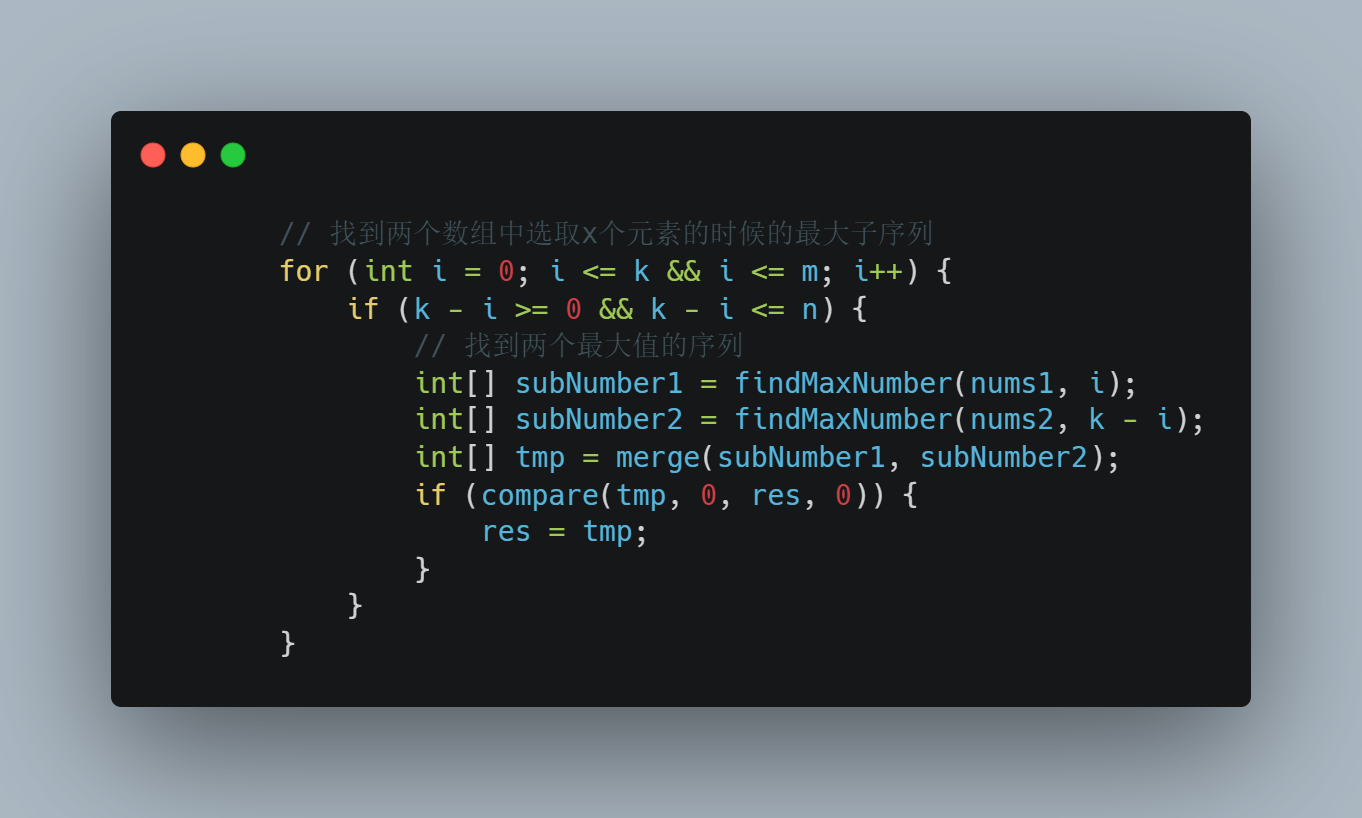
!NOTE\] 其中的`i<=m`,`k-i<=n`为什么能取到等号 众所周知,我们平常在遍历数组的时候一般都是`0~length-1`这样就是一个完整的范围,那这里为什么能取到等号呢? 首先要明白我们这个循环的目的是为了什么,它是为了从数组中选取N个元素。 * 从 `nums1` 中最多选择 `m` 个元素,也就是数组 `nums1` 的所有元素。 * 当 `i = m` 时,表示你已经选择了 `nums1` 的所有元素,而此时从 `nums2` 中选择 `k - i` 个元素。 * 所以,`i` 取到 `m` 是合理的。 *** ** * ** *** * 从 `nums2` 中最多选择 `n` 个元素,也就是数组 `nums2` 的所有元素。 * 当 `k - i = n` 时,表示你已经选择了 `nums2` 的所有元素,而此时从 `nums1` 中选择 `i = k - n` 个元素。 * 所以,`k - i` 取到 `n` 也是合理的。
2、看findMaxNumber中的这段代码
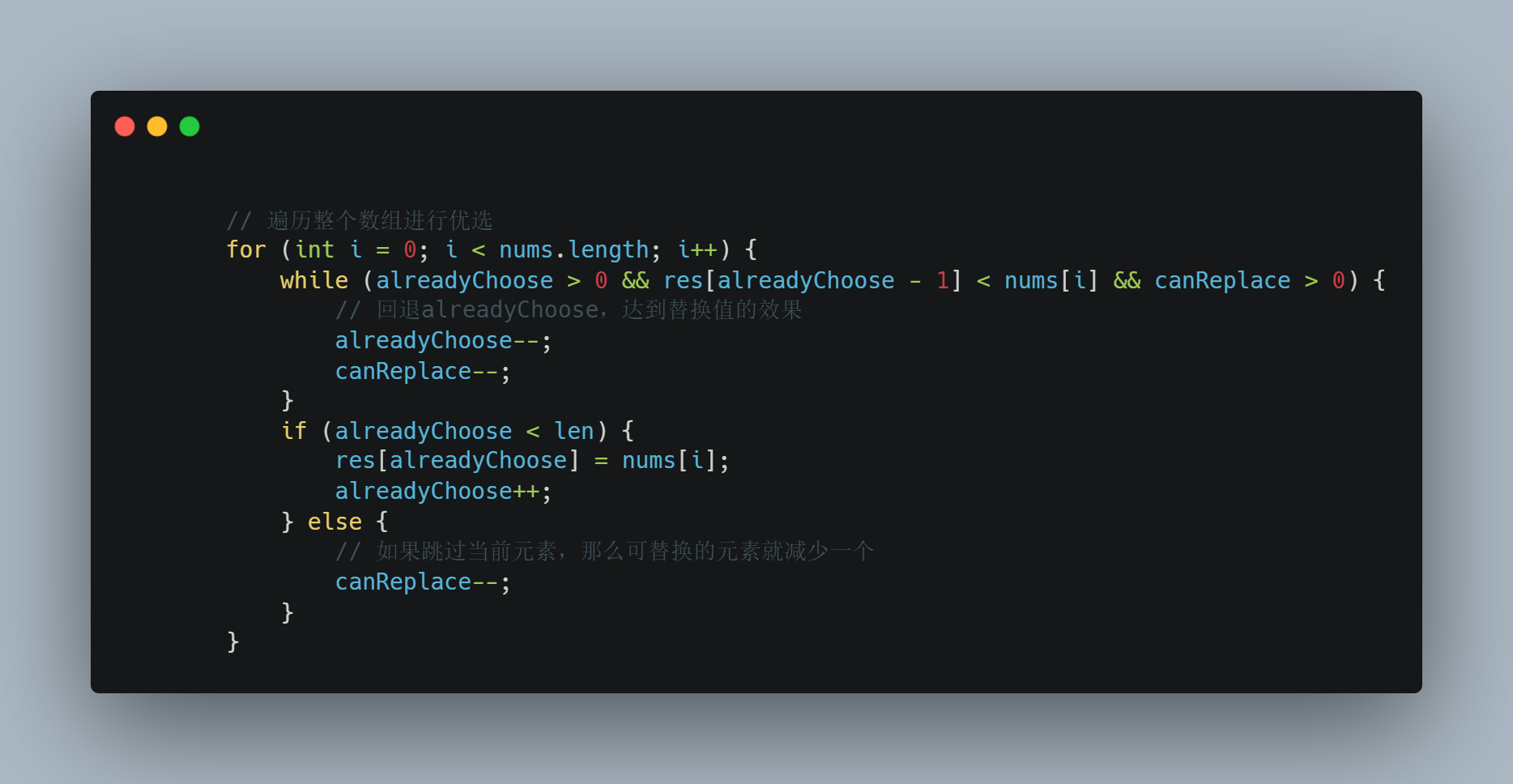
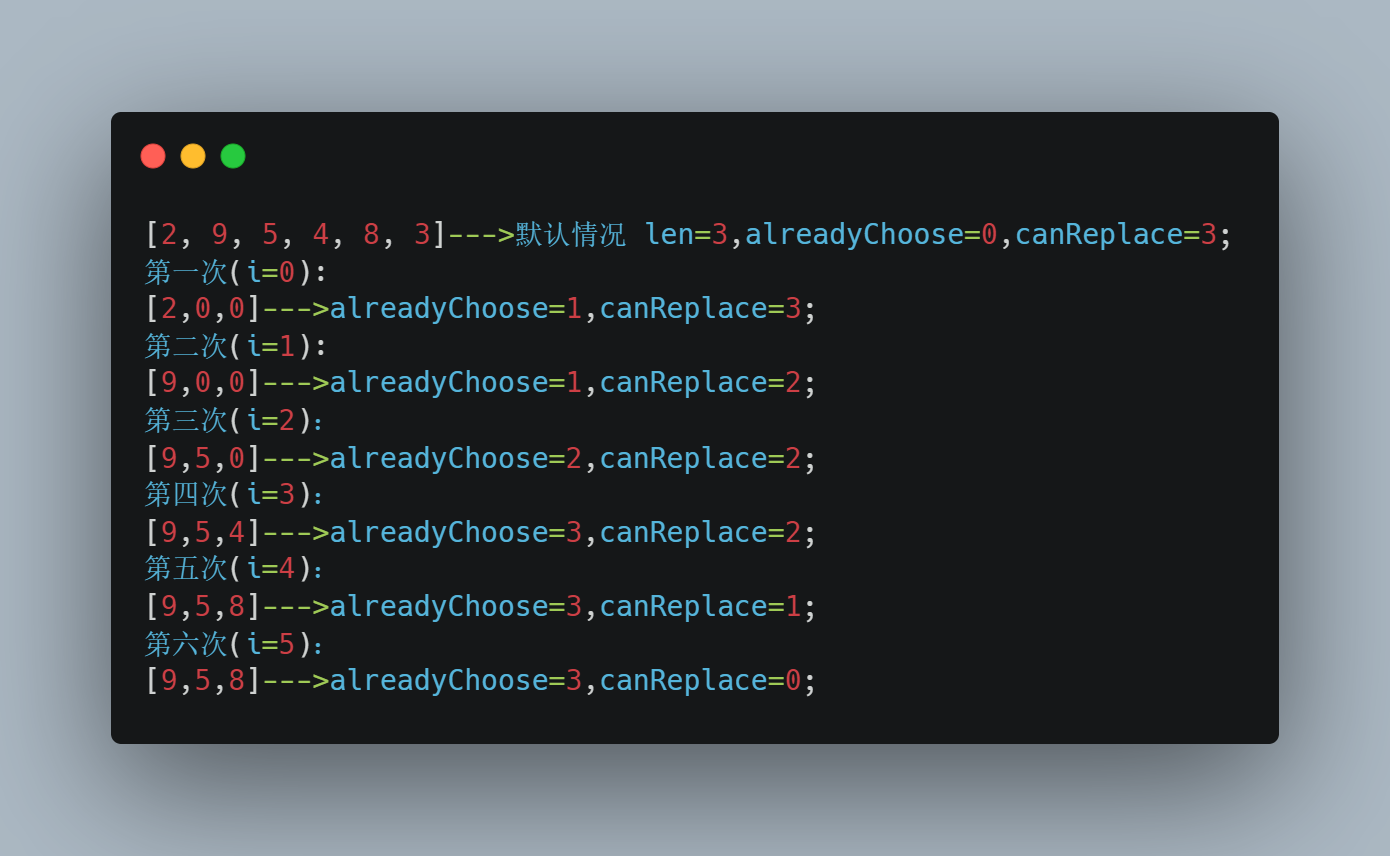
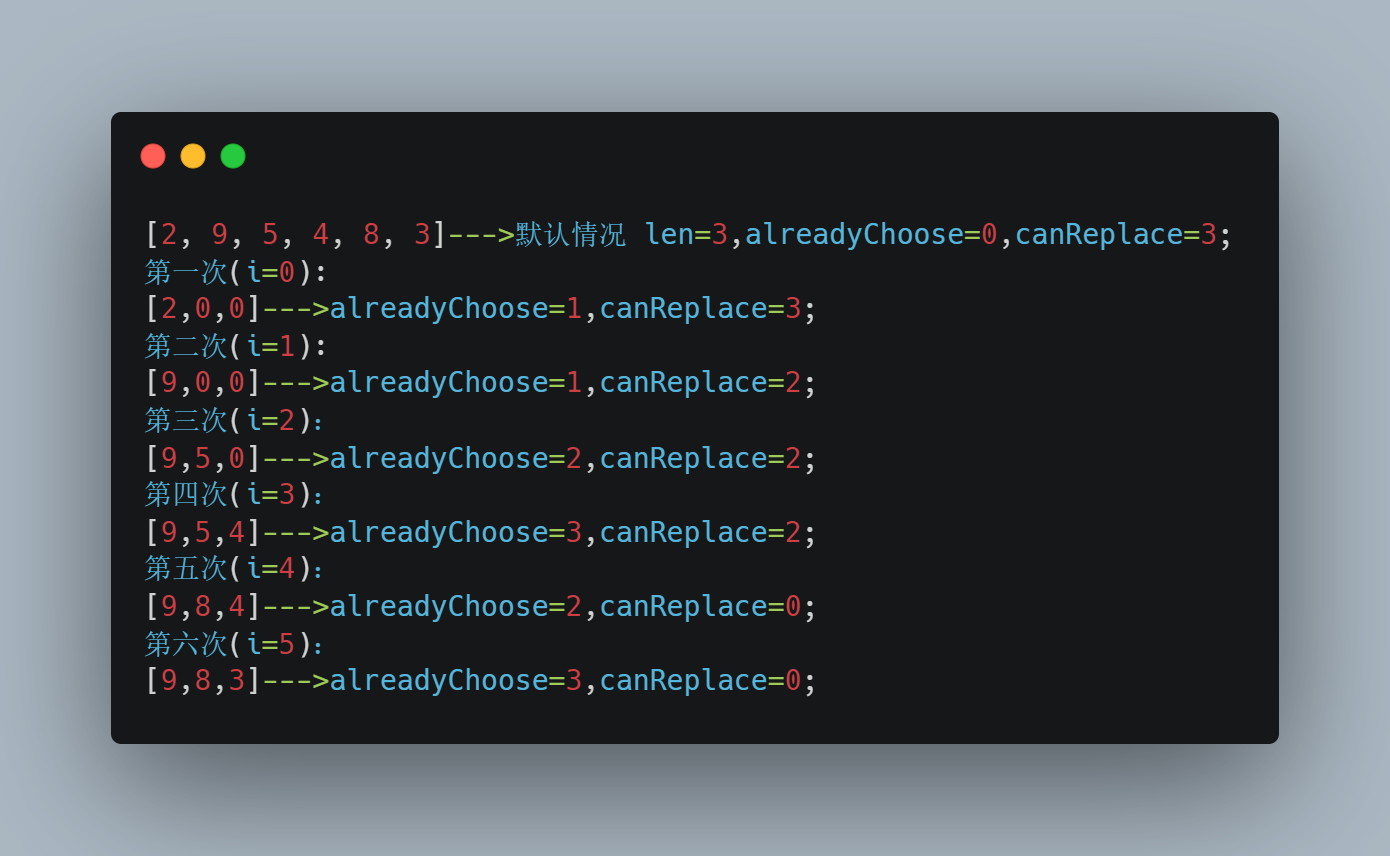
!NOTE\] Title 它的核心逻辑就是看当前选择的元素是不是比现在的元素小,如果比现在的元素小而且还有可替换的元素,那么用当前元素替换已选择元素。 其中的`canReplace`就是关键,最开始它的值是`nums.length - len`代表在选取 `len` 个元素后,尚未选中的元素数量,它们可以被用来替换当前已选中的元素,达到优化结果的目的。 在当前元素小于已选取的上个元素的时候,`canReplace--`,这是因为这个元素被跳过了,那么也就不在我们可替换的列表中了,所以`canReplace`需要减少1 \[!NOTE\] 为什么进行替换的时候要用while不用if * **`if` 语句**:只能进行一次条件判断,不适合处理需要删除多个元素的情况,因此会错过更优的选择。 * **`while` 循环**:能够处理连续的删除操作,以确保最终得到的子序列是最大的。 请看下面的例子: 数组为{2, 9, 5, 4, 8, 3} len=3。正确答案应该是\[9,8,3
首先来看if情况下
最终得到答案[9,5,8]是错误的
我们再来看while情况下:
实在没办法理解可以把代码粘贴到IDEA自己断点就能看出来了:
java
public class Test {
public static void main(String[] args) {
int[] nums = {2, 9, 5, 4, 8, 3};
int k = 3;
int[] res = findMaxNumber(nums, k);
for (int i : res) {
System.out.println(i);
}
}
public static int[] findMaxNumber(int[] nums, int len) {
int[] res = new int[len];
//已经选择了的元素个数
int alreadyChoose = 0;
//还能替换的元素个数
int canReplace = nums.length - len;
// 遍历整个数组进行优选
for (int i = 0; i < nums.length; i++) {
while (alreadyChoose > 0 && res[alreadyChoose - 1] < nums[i] && canReplace > 0) {
// 回退alreadyChoose,达到替换值的效果
alreadyChoose--;
canReplace--;
}
if (alreadyChoose < len) {
res[alreadyChoose] = nums[i];
alreadyChoose++;
} else {
// 如果跳过当前元素,那么可替换的元素就减少一个
canReplace--;
}
}
return res;
}
}3.2. 完整代码
java
class Solution {
public int[] maxNumber(int[] nums1, int[] nums2, int k) {
int m = nums1.length;
int n = nums2.length;
int[] res = new int[0];
// 找到两个数组中选取x个元素的时候的最大子序列
for (int i = 0; i <= k && i <= m; i++) {
if (k - i >= 0 && k - i <= n) {
// 找到两个最大值的序列
int[] subNumber1 = findMaxNumber(nums1, i);
int[] subNumber2 = findMaxNumber(nums2, k - i);
int[] tmp = merge(subNumber1, subNumber2);
if (compare(tmp, 0, res, 0)) {
res = tmp;
}
}
}
return res;
}
private int[] findMaxNumber(int[] nums, int len) {
int[] res = new int[len];
//已经选择了的元素个数
int alreadyChoose = 0;
//还能替换的元素个数
int canReplace = nums.length - len;
// 遍历整个数组进行优选
for (int i = 0; i < nums.length; i++) {
while (alreadyChoose > 0 && res[alreadyChoose - 1] < nums[i] && canReplace > 0) {
// 回退alreadyChoose,达到替换值的效果
alreadyChoose--;
canReplace--;
}
if (alreadyChoose < len) {
res[alreadyChoose] = nums[i];
alreadyChoose++;
} else {
// 如果跳过当前元素,那么可替换的元素就减少一个
canReplace--;
}
}
return res;
}
private int[] merge(int[] nums1, int[] nums2) {
int[] res = new int[nums1.length + nums2.length];
int cur = 0;
int p1 = 0;
int p2 = 0;
while (cur < nums1.length + nums2.length) {
// 对比下来NUM1的当前元素大于nums2
if (compare(nums1, p1, nums2, p2)) {
res[cur++] = nums1[p1++];
} else {
res[cur++] = nums2[p2++];
}
}
return res;
}
/**
* compare 函数用来比较两个数组(或者两个数组的剩余部分)哪个"更大"。
* 返回true代表num1大,否则代表nums2大
*/
private boolean compare(int[] nums1, int p1, int[] nums2, int p2) {
// nums2 用完了,nums1 更大(只能选nums1了)
if (p2 >= nums2.length) {
return true;
}
// nums1 用完了,nums2 更大(只能选nums2了)
if (p1 >= nums1.length) {
return false;
}
// nums1 当前元素大,nums1 更大
if (nums1[p1] > nums2[p2]) {
return true;
}
// nums2 当前元素大,nums2 更大
if (nums1[p1] < nums2[p2]) {
return false;
}
// 如果当前元素相等,递归比较后续的元素
return compare(nums1, p1 + 1, nums2, p2 + 1);
}
}