前述学习过程中,我们已经掌握了3D surface的基本绘制技巧,详见链接:
python画图|3D surface基础教程-CSDN博客
基础教程中的3D surface绘制位于笛卡尔坐标系,但有时候会用到极坐标绘图。虽然我们已经学过简单的极坐标绘图技巧,详见链接:
python画图|极坐标中画直方图_ax1.plot()怎么画直方图-CSDN博客
但前面的极坐标绘图学习也是基于笛卡尔坐标系。
因此,很有必要继续探索3D 极坐标系下的surface图绘制。
【1】官网教程
打开官网链接,看到漂亮的3D图:
3D surface with polar coordinates --- Matplotlib 3.9.2 documentation
很有必要,读懂官网程序。
【2】程序解读
程序开始,是亘古不变的numpy、matplotlib引入:
import matplotlib.pyplot as plt #引入matplotlib模块画图 import numpy as np #引入numpy模块做数学计算
然后设定要画图,画3D图:
fig = plt.figure() #定义要画图 ax = fig.add_subplot(projection='3d') #定义要画3D图
到这里其实都是前置条件,说明了要画图,给出了画图必须得数据计算支撑模块numpy和输出图形支撑模块matplotlib。
然后才开始定义变量:
# Create the mesh in polar coordinates and compute corresponding Z. r = np.linspace(0, 1.25, 50) #定义自变量r p = np.linspace(0, 2*np.pi, 50) #定义自变量p R, P = np.meshgrid(r, p) #自变量r和p充分组合 Z = ((R**2 - 1)**2) #定义因变量R # Express the mesh in the cartesian system. X, Y = R*np.cos(P), R*np.sin(P) #定义因变量XY
这里的meshgrid让r和p充分组合,之后:先完成了Z的定义,在完成了Z和Y的定义。
接下来输出图形:
# Plot the surface. ax.plot_surface(X, Y, Z, cmap=plt.cm.YlGnBu_r) #画surface面,颜色按照YlGnBu_r分布
最后对坐标属性进行了设定,并输出图形:
# Tweak the limits and add latex math labels. ax.set_zlim(0, 1) #设定Z轴范围 ax.set_xlabel(r'$\phi_\mathrm{real}$') #设定X轴为实轴 ax.set_ylabel(r'$\phi_\mathrm{im}$') #设定Y轴为虚轴 ax.set_zlabel(r'$V(\phi)$') #设定Z轴为角度轴 plt.show() #输出图形
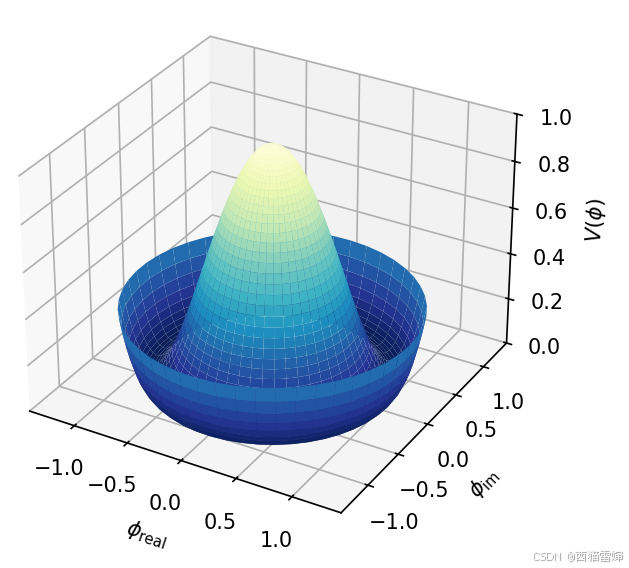
++图1++
图1即为输出图形。
至此增添注释后的完整代码为:
python
import matplotlib.pyplot as plt #引入matplotlib模块画图
import numpy as np #引入numpy模块做数学计算
fig = plt.figure() #定义要画图
ax = fig.add_subplot(projection='3d') #定义要画3D图
# Create the mesh in polar coordinates and compute corresponding Z.
r = np.linspace(0, 1.25, 50) #定义自变量r
p = np.linspace(0, 2*np.pi, 50) #定义自变量p
R, P = np.meshgrid(r, p) #自变量r和p充分组合
Z = ((R**2 - 1)**2) #定义因变量R
# Express the mesh in the cartesian system.
X, Y = R*np.cos(P), R*np.sin(P) #定义因变量XY
# Plot the surface.
ax.plot_surface(X, Y, Z, cmap=plt.cm.YlGnBu_r) #画surface面,颜色按照YlGnBu_r分布
# Tweak the limits and add latex math labels.
ax.set_zlim(0, 1) #设定Z轴范围
ax.set_xlabel(r'$\phi_\mathrm{real}$') #设定X轴为实轴
ax.set_ylabel(r'$\phi_\mathrm{im}$') #设定Y轴为虚轴
ax.set_zlabel(r'$V(\phi)$') #设定Z轴为角度轴
plt.show() #输出图形【3】修改代码
cmap=plt.cm.YlGnBu_r为渐变式的上色,color为纯色。画图结果为:
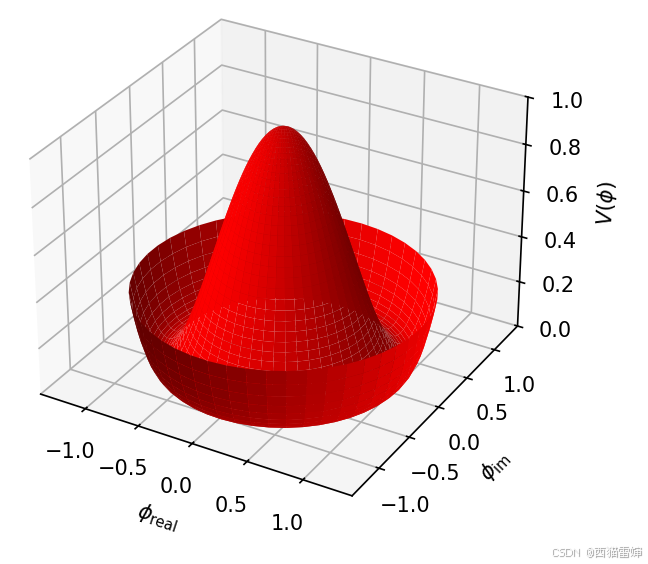
++图2++
由图2课件,整个图形已经更换为红色。
【4】改写代码
改写代码,实现:
【a】并列输出多个图形;
【b】设定不同颜色的输出。
首先,将fig定义改为subplots形式,并约定每个子模型都画3D图:
fig ,[ax1,ax2,ax3]= plt.subplots(1,3,sharey=True,figsize=(6,2)) #定义要画图 ax1 = fig.add_subplot(1,3,1,projection='3d') #定义要画3D图 ax2 = fig.add_subplot(1,3,2,projection='3d') #定义要画3D图 ax3 = fig.add_subplot(1,3,3,projection='3d') #定义要画3D图
然后,修改画图plot_surface模块中的颜色指定:
ax1.plot_surface(X, Y, Z, cmap=plt.cm.PuBuGn) #画surface面,颜色按照PuBuGn分布 ax2.plot_surface(X, Y, Z, color='r') #画surface面,颜色为红色 ax3.plot_surface(X, Y, Z, color='g') #画surface面,颜色为绿色
此时的结果为:
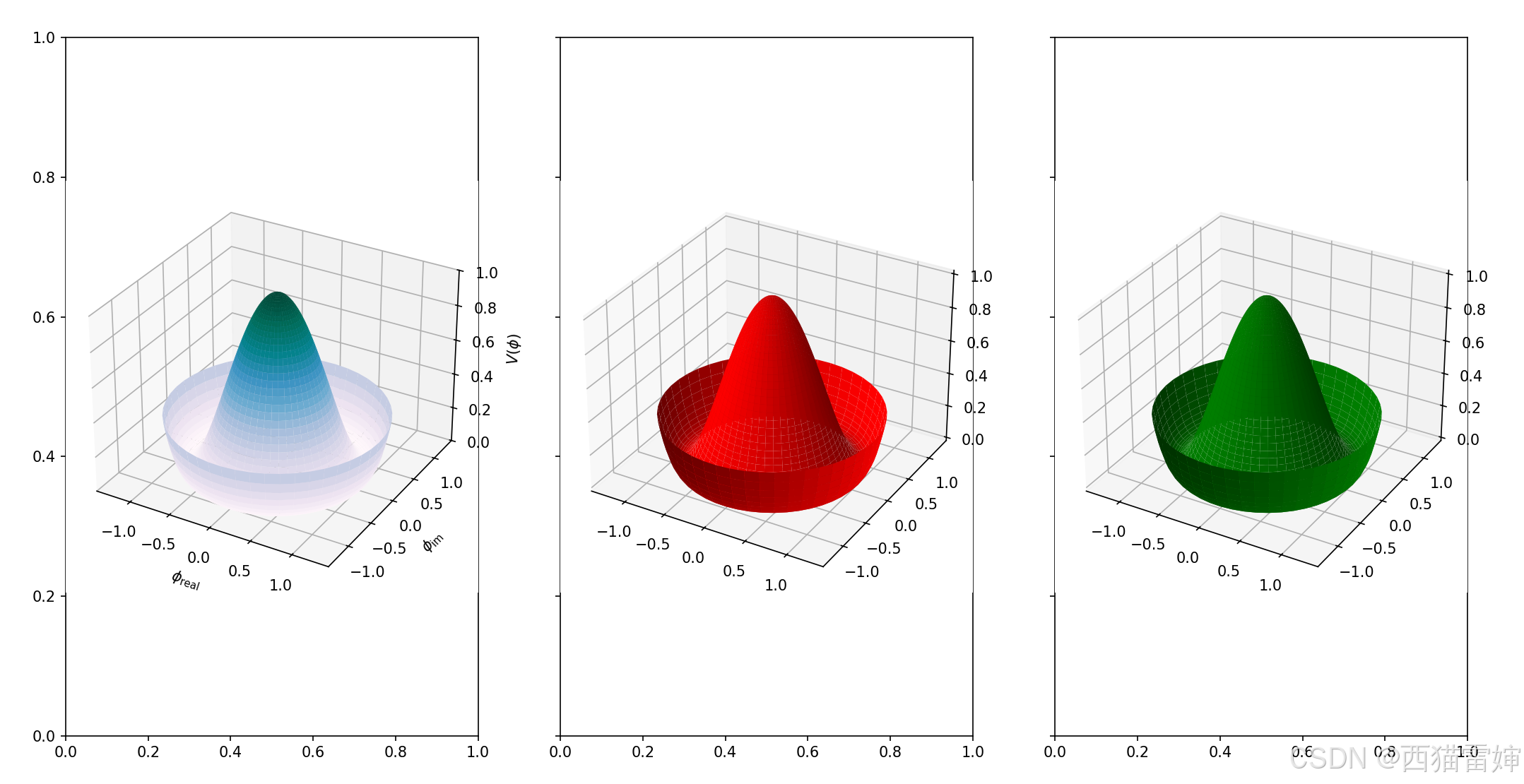
++图3++
图3即为并列输出结果,此时只有最左侧图形为渐变色。这里使用了PuBuGn代码,这个代码代表了一种新的渐变,详情可参考下述链接:
Choosing Colormaps in Matplotlib --- Matplotlib 3.9.2 documentation
上图3中,似乎渐变图是最好看的,参考上述链接,修改颜色代码后:
# Plot the surface. ax1.plot_surface(X, Y, Z, cmap=plt.cm.PuBuGn) #画surface面,颜色按照PuBuGn分布 ax2.plot_surface(X, Y, Z, cmap='Accent') #画surface面,颜色为v ax3.plot_surface(X, Y, Z, cmap='summer_r') #画surface面,颜色为summer_r
此时的输出结果为:
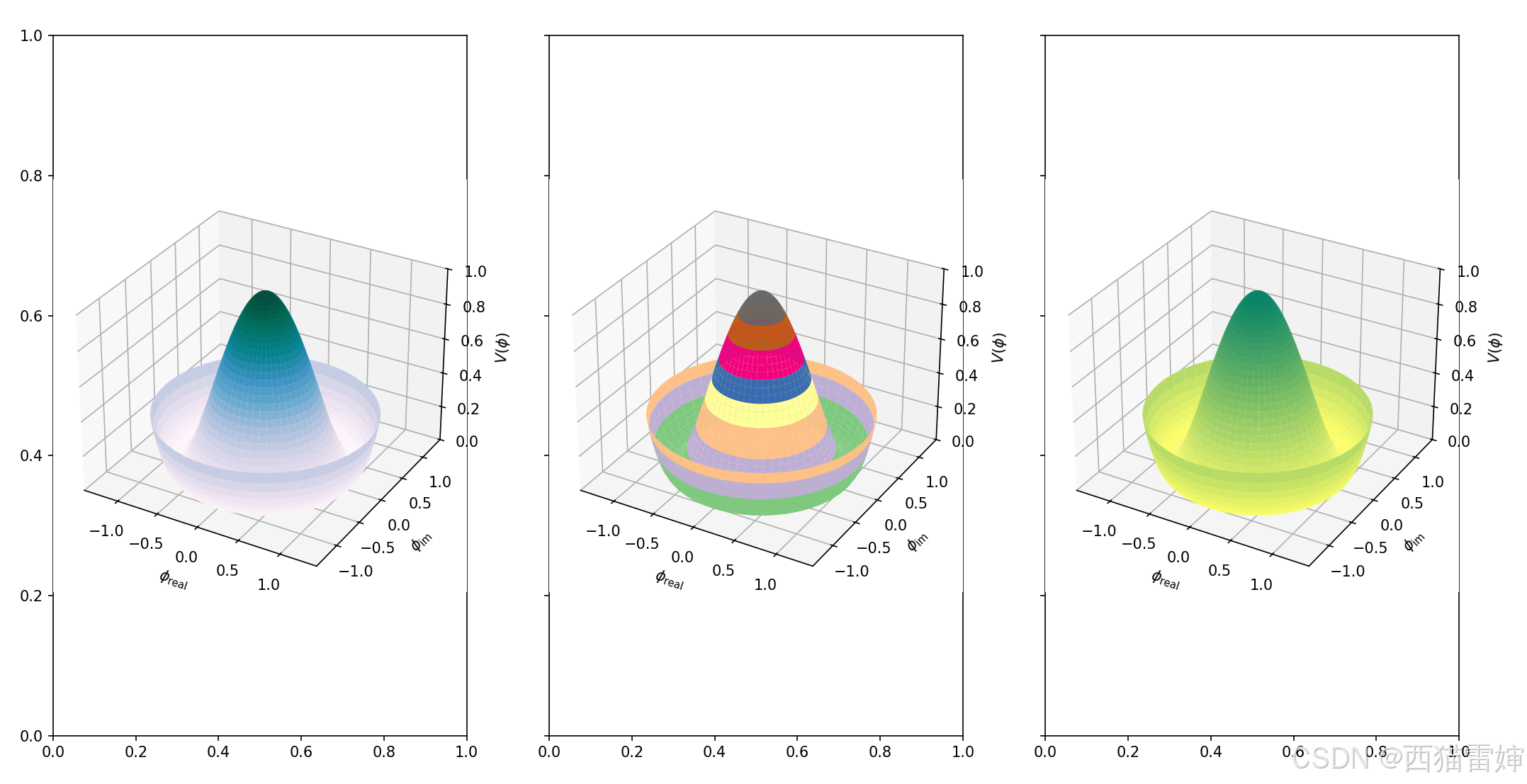
++图4++
由图4可见,不同颜色的表达给人的感觉不同。
为精益求精,尝试把每个图的方框去掉,并且加上图名:
改后的执行去除方框功能和附近其他代码为:
fig ,[ax1,ax2,ax3]= plt.subplots(1,3,sharey=True,figsize=(6,2)) #定义要画图 fig.delaxes(ax1) #去除方框 fig.delaxes(ax2) #去除方框 fig.delaxes(ax3) #去除方框
增加图名代码为:
# Tweak the limits and add latex math labels. ax1.set_title(label='cmap=plt.cm.PuBuGn' ) ax2.set_title(label='cmap=Accent' ) ax3.set_title(label='cmap=summer_r' )
输出图形为:
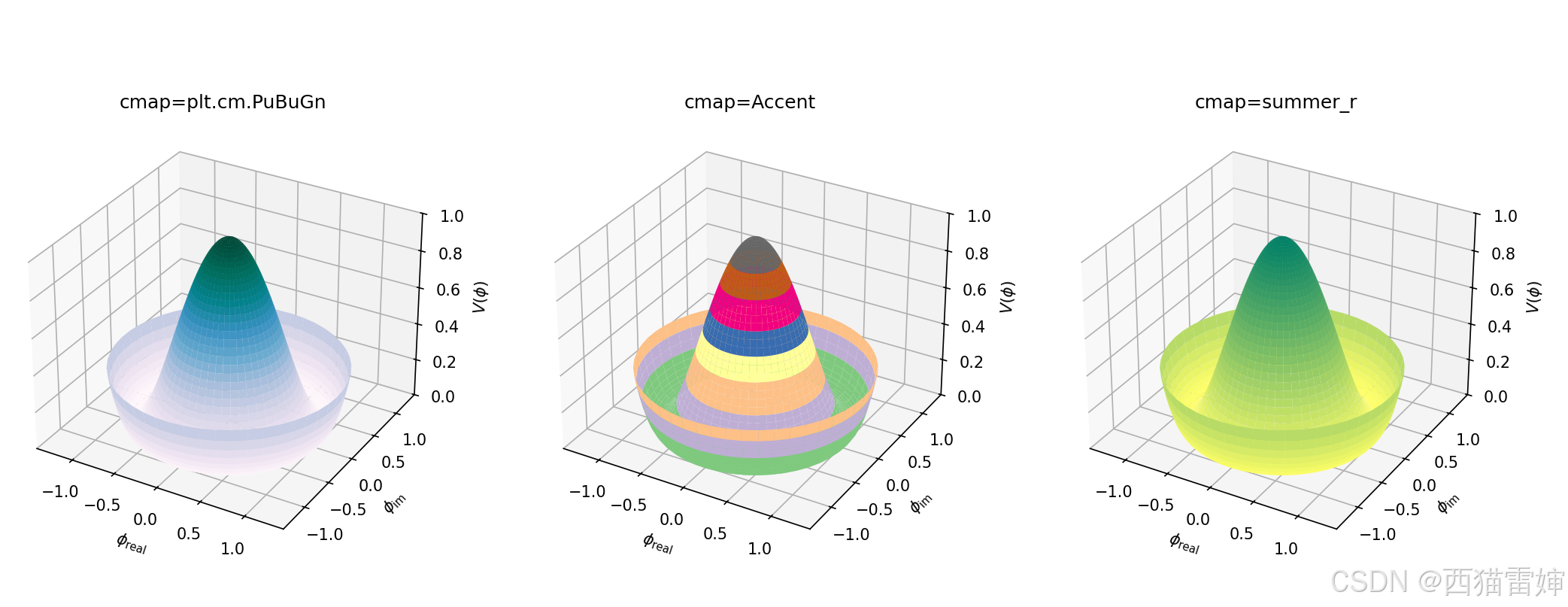
++图5++
图5即为无方框、带图名并列输出结果。
【5】总结
学习了极坐标下的3D surface画法,尝试修改了图形颜色,掌握了多个图形输出的方法,掌握了图形方框和图名设置方法。