[atcoder agc 004 c] AND Grid

题目链接

题目简述

给定一个 H × W H \times W H×W 的网格图，有些位置已经被涂色。要求构造两个相同大小的网格图，并且在上面涂色，需要保证颜色四联通。满足这两个网格的涂色部分的重合位置恰好是给定的网格图的涂色位置。

题目保证边界上不会被涂色。即对于第 1 1 1 行、第 1 1 1 列、第 H H H 行、第 W W W 列，都不会有 # 出现。

输入格式

第一行两个整数 H H H 和 W W W。

接下来 H H H 行，每行 W W W 个字符，表示 ( i , j ) (i, j) (i,j) 的位置是否涂色。

输出格式

输出两个 H × W H \times W H×W 的字符矩阵。

样例

样例输入1：

5 5
.....
.#.#.
.....
.#.#.
.....

样例输出1：

.....
#####
#....
#####
.....

.###.
.#.#.
.#.#.
.#.#.
.....

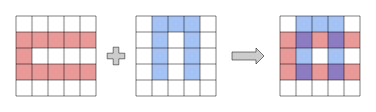
样例解释1：

样例输入2：

7 13
.............
.###.###.###.
.#.#.#...#...
.###.#...#...
.#.#.#.#.#...
.#.#.###.###.
.............

样例输出2：

.............
.###########.
.###.###.###.
.###.###.###.
.###.###.###.
.###.###.###.
.............

.............
.###.###.###.
.#.#.#...#...
.###.#...#...
.#.#.#.#.#...
.#.#########.
.............

样例解释2：

数据范围

3 ≤ H , W ≤ 500 3 \le H, W \le 500 3≤H,W≤500
a i , j a_{i, j} ai,j 为 # 或 . 且 a 1 , j , a H , j , a i , 1 , a i , W a_{1, j}, a_{H, j}, a_{i, 1}, a_{i, W} a1,j,aH,j,ai,1,ai,W 为 .。

题解

这道题主要是怎么构造两个矩阵的问题。

1

由于第 1 1 1 行、第 1 1 1 列、第 H H H 行、第 W W W 列都不会涂色，所以我们可以从这几行（或列）进行考虑。

以用第 1 1 1 列和第 W W W 列为例，先将第 1 1 1 个矩阵的第 1 1 1 列涂色，第 2 2 2 个矩阵的第 W W W 列涂色。

由于图案要求四联通，所以可以将第 1 1 1 个矩阵的奇数行涂色，第 2 2 2 个矩阵的偶数行涂色，这样就能将所有图案四联通了。

cpp 复制代码

n 是题目中的 H, m 是题目中的 W
a, b 是两个矩阵
输入矩阵 a
for(int i = 1; i <= n; ++ i){
	for(int j = 1; j <= m; ++ j){
		b[i][j] = a[i][j];
	}
}
for(int i = 1; i <= n; i += 2){
	for(int j = 2; j < m; ++ j){
		a[i][j] = '#';
	}
}
for(int i = 2; i <= n; i += 2){
	for(int j = 2; j < m; ++ j){
		b[i][j] = '#';
	}
}
for(int i = 1; i <= n; ++ i){
	a[i][1] = '#';
}
for(int i = 1; i <= n; ++ i){
	b[i][m] = '#';
}
输出 a 和 b

2

还可以构造蛇形矩阵，可以不用四边不涂色的条件（但是四个角不能有），具体见 agc004c。

禁止抄袭!!!