完全二叉树的节点个数

Given the root of a complete binary tree, return the number of the nodes in the tree.

According to Wikipedia , every level, except possibly the last, is completely filled in a complete binary tree, and all nodes in the last level are as far left as possible. It can have between 1 and 2h nodes inclusive at the last level h.

Design an algorithm that runs in less than O(n) time complexity.

Example 1:

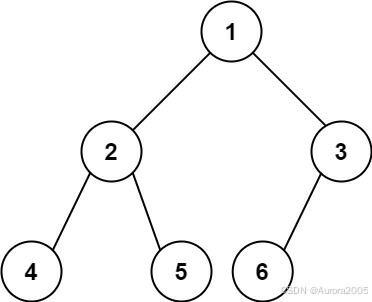
Input: root = [1,2,3,4,5,6]
Output: 6

Example 2:

Input: root = []
Output: 0

Example 3:

Input: root = [1]
Output: 1

Constraints:

• The number of nodes in the tree is in the range [0, 5 * 104].

• 0 <= Node.val <= 5 * 104

• The tree is guaranteed to be complete.

  class Solution {
  public:
  int countNodes(TreeNode* root) {
  if(root==NULL)return 0;
  TreeNodeleftNode=root->left;
  TreeNoderightNode=root->right;
  int leftDepth=0,rightDepth=0;
  while(leftNode){
  leftNode=leftNode->left;
  leftDepth++;
  }
  while(rightNode){
  rightNode=rightNode->right;
  rightDepth++;
  }
  if(leftDepth==rightDepth){
  return (2<<leftDepth)-1;
  }
  return countNodes(root->left)+countNodes(root->right)+1;//后序遍历的精简
  }
  };

思路：

1，计算完全二叉树节点的公式：满二叉树就可以直接2*2^depth-1

2，那问题来了，怎么判断是否为满二叉树呢？遍历得到左右两边的深度，leftDepth==rightDepth就是满二叉树（Ps：这种不是完全二叉树------完全二叉树除了最低级别的以外都是满的，尽可能满足左子树）

3，那如果不是满二叉树怎么求呢？------后序递归求得各个完全二叉子树的节点数相加，后+1（根节点）