LeetCode 427. 建立四叉树

（题干略）

python 复制代码

"""
# Definition for a QuadTree node.
class Node:
    def __init__(self, val, isLeaf, topLeft, topRight, bottomLeft, bottomRight):
        self.val = val
        self.isLeaf = isLeaf
        self.topLeft = topLeft
        self.topRight = topRight
        self.bottomLeft = bottomLeft
        self.bottomRight = bottomRight
"""


class Solution:
    def construct(self, grid: List[List[int]]) -> "Node":
        return self._construct(grid, 0, 0, len(grid) - 1, len(grid[0]) - 1)

    def _construct(
        self, grid: List[List[int]], x1: int, y1: int, x2: int, y2: int
    ) -> "Node":
        q = (
            x2 - x1 + 1
        ) >> 1  # 给定正方形中四分之一正方形的边长，特别地，q == 0 时，表示该正方形不可再分
        if not q:
            return Node(grid[x1][y1], True, None, None, None, None)
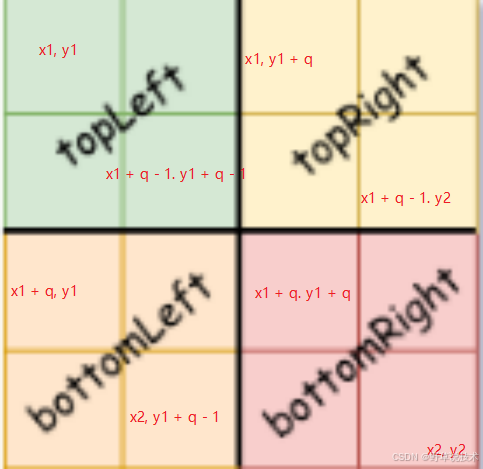
        topLeft = self._construct(grid, x1, y1, x1 + q - 1, y1 + q - 1)
        topRight = self._construct(grid, x1, y1 + q, x1 + q - 1, y2)
        bottomLeft = self._construct(grid, x1 + q, y1, x2, y1 + q - 1)
        bottomRight = self._construct(grid, x1 + q, y1 + q, x2, y2)
        # 有四个叶子节点，且值相同就向上合并为新的叶子节点
        if (
            topLeft.isLeaf
            and topRight.isLeaf
            and bottomLeft.isLeaf
            and bottomRight.isLeaf
            and topLeft.val == topRight.val == bottomLeft.val == bottomRight.val
        ):
            return Node(topLeft.val, True, None, None, None, None)
        else:
            return Node(0, False, topLeft, topRight, bottomLeft, bottomRight)

时间复杂度

本题是经典的基于分治思想写出的递归解法，假设每个边长为n的矩形区域耗时为T(n)，显然T(1) = O(1)，则 T(n) = 4 T(n/2) + O(1)，根据主定理可以求得时间复杂度为 O(n^2)

空间复杂度

空间复杂度为递归所占用的最大栈深度，算法整个栈的搜索空间为一颗完全四叉树，最深层的叶子节点为n^2个，最大栈深度就是二叉树的高度，有公式 4^(h-1) = n^2，则空间复杂度为 O(logn)