Leetcode: 0001-0010题速览
研一在读备战就业,制此集合便于空闲时间浏览,有任何疑惑问题欢迎讨论,共同进步
目录
- [Leetcode: 0001-0010题速览](#Leetcode: 0001-0010题速览)
-
- [[1. 两数之和](https://leetcode.cn/problems/two-sum)](#1. 两数之和)
- [[2. 两数相加](https://leetcode.cn/problems/add-two-numbers)](#2. 两数相加)
- [[3. 无重复字符的最长子串](https://leetcode.cn/problems/longest-substring-without-repeating-characters)](#3. 无重复字符的最长子串)
- [[4. 寻找两个正序数组的中位数](https://leetcode.cn/problems/median-of-two-sorted-arrays)](#4. 寻找两个正序数组的中位数)
- [[5. 最长回文子串](https://leetcode.cn/problems/longest-palindromic-substring)](#5. 最长回文子串)
- [[6. Z 字形变换](https://leetcode.cn/problems/zigzag-conversion)](#6. Z 字形变换)
- [[7. 整数反转](https://leetcode.cn/problems/reverse-integer)](#7. 整数反转)
- [[8. 字符串转换整数 (atoi)](https://leetcode.cn/problems/string-to-integer-atoi)](#8. 字符串转换整数 (atoi))
- [[9. 回文数](https://leetcode.cn/problems/palindrome-number)](#9. 回文数)
- [[10. 正则表达式匹配](https://leetcode.cn/problems/regular-expression-matching)](#10. 正则表达式匹配)
1. 两数之和
题目描述
给定一个整数数组 nums 和一个整数目标值 target,请你在该数组中找出 和为目标值 target 的那 两个 整数,并返回它们的数组下标。
你可以假设每种输入只会对应一个答案,并且你不能使用两次相同的元素。
你可以按任意顺序返回答案。
示例 1:
输入: nums = [2,7,11,15], target = 9
输出: [0,1]
**解释:**因为 nums[0] + nums[1] == 9 ,返回 [0, 1] 。
示例 2:
输入: nums = [3,2,4], target = 6
输出:[1,2]
示例 3:
输入: nums = [3,3], target = 6
输出:[0,1]
提示:
2 <= nums.length <= 104-109<= nums[i] <= 109-109<= target <= 109- 只会存在一个有效答案
进阶: 你可以想出一个时间复杂度小于 O(n2) 的算法吗?
难度:简单
标签:数组,哈希表
解法
方法一:哈希表
我们可以使用一个哈希表 d \textit{d} d 来存储每个元素及其对应的索引。
遍历数组 nums \textit{nums} nums,对于当前元素 nums [ i ] \textit{nums}[i] nums[i],我们首先判断 target − nums [ i ] \textit{target} - \textit{nums}[i] target−nums[i] 是否在哈希表 d \textit{d} d 中,如果在 d \textit{d} d 中,说明 target \textit{target} target 值已经找到,返回 target − nums [ i ] \textit{target} - \textit{nums}[i] target−nums[i] 的索引和 i i i 即可。
时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( n ) O(n) O(n),其中 n n n 为数组 nums \textit{nums} nums 的长度。
Python3
python
class Solution:
def twoSum(self, nums: List[int], target: int) -> List[int]:
d = {}
for i, x in enumerate(nums):
y = target - x
if y in d:
return [d[y], i]
d[x] = iJava
java
class Solution {
public int[] twoSum(int[] nums, int target) {
Map<Integer, Integer> d = new HashMap<>();
for (int i = 0;; ++i) {
int x = nums[i];
int y = target - x;
if (d.containsKey(y)) {
return new int[] {d.get(y), i};
}
d.put(x, i);
}
}
}C++
cpp
class Solution {
public:
vector<int> twoSum(vector<int>& nums, int target) {
unordered_map<int, int> d;
for (int i = 0;; ++i) {
int x = nums[i];
int y = target - x;
if (d.contains(y)) {
return {d[y], i};
}
d[x] = i;
}
}
};2. 两数相加
题目描述
给你两个 非空 的链表,表示两个非负的整数。它们每位数字都是按照 逆序 的方式存储的,并且每个节点只能存储 一位 数字。
请你将两个数相加,并以相同形式返回一个表示和的链表。
你可以假设除了数字 0 之外,这两个数都不会以 0 开头。
示例 1:
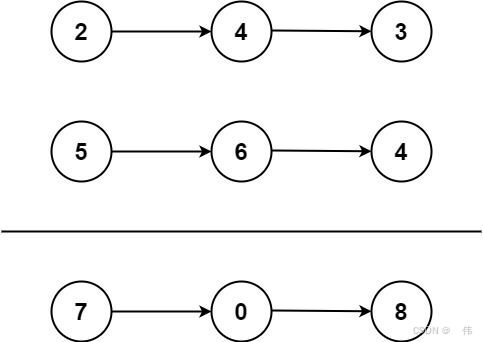
输入: l1 = [2,4,3], l2 = [5,6,4]
输出: [7,0,8]
**解释:**342 + 465 = 807.
示例 2:
输入: l1 = [0], l2 = [0]
输出:[0]
示例 3:
输入: l1 = [9,9,9,9,9,9,9], l2 = [9,9,9,9]
输出:[8,9,9,9,0,0,0,1]
提示:
- 每个链表中的节点数在范围
[1, 100]内 0 <= Node.val <= 9- 题目数据保证列表表示的数字不含前导零
难度:中等
标签:递归,链表,数学
解法
方法一:模拟
我们同时遍历两个链表 l 1 l_1 l1 和 l 2 l_2 l2,并使用变量 c a r r y carry carry 表示当前是否有进位。
每次遍历时,我们取出对应链表的当前位,计算它们与进位 c a r r y carry carry 的和,然后更新进位的值,最后将当前位的值加入答案链表。如果两个链表都遍历完了,并且进位为 0 0 0 时,遍历结束。
最后我们返回答案链表的头节点即可。
时间复杂度 O ( max ( m , n ) ) O(\max(m, n)) O(max(m,n)),其中 m m m 和 n n n 分别为两个链表的长度。我们需要遍历两个链表的全部位置,而处理每个位置只需要 O ( 1 ) O(1) O(1) 的时间。忽略答案的空间消耗,空间复杂度 O ( 1 ) O(1) O(1)。
Python3
python
## Definition for singly-linked list.
## class ListNode:
## def __init__(self, val=0, next=None):
## self.val = val
## self.next = next
class Solution:
def addTwoNumbers(
self, l1: Optional[ListNode], l2: Optional[ListNode]
) -> Optional[ListNode]:
dummy = ListNode()
carry, curr = 0, dummy
while l1 or l2 or carry:
s = (l1.val if l1 else 0) + (l2.val if l2 else 0) + carry
carry, val = divmod(s, 10)
curr.next = ListNode(val)
curr = curr.next
l1 = l1.next if l1 else None
l2 = l2.next if l2 else None
return dummy.nextJava
java
/**
* Definition for singly-linked list.
* public class ListNode {
* int val;
* ListNode next;
* ListNode() {}
* ListNode(int val) { this.val = val; }
* ListNode(int val, ListNode next) { this.val = val; this.next = next; }
* }
*/
class Solution {
public ListNode addTwoNumbers(ListNode l1, ListNode l2) {
ListNode dummy = new ListNode(0);
int carry = 0;
ListNode cur = dummy;
while (l1 != null || l2 != null || carry != 0) {
int s = (l1 == null ? 0 : l1.val) + (l2 == null ? 0 : l2.val) + carry;
carry = s / 10;
cur.next = new ListNode(s % 10);
cur = cur.next;
l1 = l1 == null ? null : l1.next;
l2 = l2 == null ? null : l2.next;
}
return dummy.next;
}
}C++
cpp
/**
* Definition for singly-linked list.
* struct ListNode {
* int val;
* ListNode *next;
* ListNode() : val(0), next(nullptr) {}
* ListNode(int x) : val(x), next(nullptr) {}
* ListNode(int x, ListNode *next) : val(x), next(next) {}
* };
*/
class Solution {
public:
ListNode* addTwoNumbers(ListNode* l1, ListNode* l2) {
ListNode* dummy = new ListNode();
int carry = 0;
ListNode* cur = dummy;
while (l1 || l2 || carry) {
int s = (l1 ? l1->val : 0) + (l2 ? l2->val : 0) + carry;
carry = s / 10;
cur->next = new ListNode(s % 10);
cur = cur->next;
l1 = l1 ? l1->next : nullptr;
l2 = l2 ? l2->next : nullptr;
}
return dummy->next;
}
};3. 无重复字符的最长子串
题目描述
给定一个字符串 s ,请你找出其中不含有重复字符的 最长 子串 的长度。
示例 1:
输入: s = "abcabcbb"
输出: 3
解释: 因为无重复字符的最长子串是 "abc",所以其长度为 3。
示例 2:
输入: s = "bbbbb"
输出: 1
解释: 因为无重复字符的最长子串是 "b",所以其长度为 1。
示例 3:
输入: s = "pwwkew"
输出: 3
解释: 因为无重复字符的最长子串是 "wke",所以其长度为 3。
请注意,你的答案必须是 子串 的长度,"pwke" 是一个*子序列,*不是子串。
提示:
0 <= s.length <= 5 * 104s由英文字母、数字、符号和空格组成
难度:中等
标签:哈希表,字符串,滑动窗口
解法
方法一:双指针 + 哈希表
定义一个哈希表记录当前窗口内出现的字符,记 i i i 和 j j j 分别表示不重复子串的开始位置和结束位置,无重复字符子串的最大长度记为 ans。
遍历字符串 s 的每个字符 s [ j ] s[j] s[j],我们记为 c c c。若 s [ i . . j − 1 ] s[i..j-1] s[i..j−1] 窗口内存在 c c c,则 i i i 循环向右移动,更新哈希表,直至 s [ i . . j − 1 ] s[i..j-1] s[i..j−1] 窗口不存在 c,循环结束。将 c 加入哈希表中,此时 s [ i . . j ] s[i..j] s[i..j] 窗口内不含重复元素,更新 ans 的最大值。
最后返回 ans 即可。
时间复杂度 O ( n ) O(n) O(n),其中 n n n 表示字符串 s 的长度。
双指针算法模板:
java
for (int i = 0, j = 0; i < n; ++i) {
while (j < i && check(j, i)) {
++j;
}
// 具体问题的逻辑
}Python3
python
class Solution:
def lengthOfLongestSubstring(self, s: str) -> int:
ss = set()
ans = i = 0
for j, c in enumerate(s):
while c in ss:
ss.remove(s[i])
i += 1
ss.add(c)
ans = max(ans, j - i + 1)
return ansJava
java
class Solution {
public int lengthOfLongestSubstring(String s) {
boolean[] ss = new boolean[128];
int ans = 0;
for (int i = 0, j = 0; j < s.length(); ++j) {
char c = s.charAt(j);
while (ss[c]) {
ss[s.charAt(i++)] = false;
}
ss[c] = true;
ans = Math.max(ans, j - i + 1);
}
return ans;
}
}C++
cpp
class Solution {
public:
int lengthOfLongestSubstring(string s) {
bool ss[128]{};
int ans = 0;
for (int i = 0, j = 0; j < s.size(); ++j) {
while (ss[s[j]]) {
ss[s[i++]] = false;
}
ss[s[j]] = true;
ans = max(ans, j - i + 1);
}
return ans;
}
};4. 寻找两个正序数组的中位数
题目描述
给定两个大小分别为 m 和 n 的正序(从小到大)数组 nums1 和 nums2。请你找出并返回这两个正序数组的 中位数 。
算法的时间复杂度应该为 O(log (m+n)) 。
示例 1:
输入: nums1 = [1,3], nums2 = [2]
输出: 2.00000
**解释:**合并数组 = [1,2,3] ,中位数 2
示例 2:
输入: nums1 = [1,2], nums2 = [3,4]
输出: 2.50000
**解释:**合并数组 = [1,2,3,4] ,中位数 (2 + 3) / 2 = 2.5
提示:
nums1.length == mnums2.length == n0 <= m <= 10000 <= n <= 10001 <= m + n <= 2000-106<= nums1[i], nums2[i] <= 106
难度:困难
标签:数组,二分查找,分治
解法
方法一:分治
题目要求算法的时间复杂度为 O ( log ( m + n ) ) O(\log (m + n)) O(log(m+n)),因此不能直接遍历两个数组,而是需要使用二分查找的方法。
如果 m + n m + n m+n 是奇数,那么中位数就是第 ⌊ m + n + 1 2 ⌋ \left\lfloor\frac{m + n + 1}{2}\right\rfloor ⌊2m+n+1⌋ 个数;如果 m + n m + n m+n 是偶数,那么中位数就是第 ⌊ m + n + 1 2 ⌋ \left\lfloor\frac{m + n + 1}{2}\right\rfloor ⌊2m+n+1⌋ 和第 ⌊ m + n + 2 2 ⌋ \left\lfloor\frac{m + n + 2}{2}\right\rfloor ⌊2m+n+2⌋ 个数的平均数。实际上,我们可以统一为求第 ⌊ m + n + 1 2 ⌋ \left\lfloor\frac{m + n + 1}{2}\right\rfloor ⌊2m+n+1⌋ 个数和第 ⌊ m + n + 2 2 ⌋ \left\lfloor\frac{m + n + 2}{2}\right\rfloor ⌊2m+n+2⌋ 个数的平均数。
因此,我们可以设计一个函数 f ( i , j , k ) f(i, j, k) f(i,j,k),表示在数组 n u m s 1 nums1 nums1 的区间 [ i , m ) [i, m) [i,m) 和数组 n u m s 2 nums2 nums2 的区间 [ j , n ) [j, n) [j,n) 中,求第 k k k 小的数。那么中位数就是 f ( 0 , 0 , ⌊ m + n + 1 2 ⌋ ) f(0, 0, \left\lfloor\frac{m + n + 1}{2}\right\rfloor) f(0,0,⌊2m+n+1⌋) 和 f ( 0 , 0 , ⌊ m + n + 2 2 ⌋ ) f(0, 0, \left\lfloor\frac{m + n + 2}{2}\right\rfloor) f(0,0,⌊2m+n+2⌋) 的平均数。
函数 f ( i , j , k ) f(i, j, k) f(i,j,k) 的实现思路如下:
- 如果 i ≥ m i \geq m i≥m,说明数组 n u m s 1 nums1 nums1 的区间 [ i , m ) [i, m) [i,m) 为空,因此直接返回 n u m s 2 [ j + k − 1 ] nums2[j + k - 1] nums2[j+k−1];
- 如果 j ≥ n j \geq n j≥n,说明数组 n u m s 2 nums2 nums2 的区间 [ j , n ) [j, n) [j,n) 为空,因此直接返回 n u m s 1 [ i + k − 1 ] nums1[i + k - 1] nums1[i+k−1];
- 如果 k = 1 k = 1 k=1,说明要找第一个数,因此只需要返回 n u m s 1 [ i ] nums1[i] nums1[i] 和 n u m s 2 [ j ] nums2[j] nums2[j] 中的最小值;
- 否则,我们分别在两个数组中查找第 ⌊ k 2 ⌋ \left\lfloor\frac{k}{2}\right\rfloor ⌊2k⌋ 个数,设为 x x x 和 y y y。(注意,如果某个数组不存在第 ⌊ k 2 ⌋ \left\lfloor\frac{k}{2}\right\rfloor ⌊2k⌋ 个数,那么我们将第 ⌊ k 2 ⌋ \left\lfloor\frac{k}{2}\right\rfloor ⌊2k⌋ 个数视为 + ∞ +\infty +∞。)比较 x x x 和 y y y 的大小:
- 如果 x ≤ y x \leq y x≤y,则说明数组 n u m s 1 nums1 nums1 的第 ⌊ k 2 ⌋ \left\lfloor\frac{k}{2}\right\rfloor ⌊2k⌋ 个数不可能是第 k k k 小的数,因此我们可以排除数组 n u m s 1 nums1 nums1 的区间 [ i , i + ⌊ k 2 ⌋ ) [i, i + \left\lfloor\frac{k}{2}\right\rfloor) [i,i+⌊2k⌋),递归调用 f ( i + ⌊ k 2 ⌋ , j , k − ⌊ k 2 ⌋ ) f(i + \left\lfloor\frac{k}{2}\right\rfloor, j, k - \left\lfloor\frac{k}{2}\right\rfloor) f(i+⌊2k⌋,j,k−⌊2k⌋)。
- 如果 x > y x > y x>y,则说明数组 n u m s 2 nums2 nums2 的第 ⌊ k 2 ⌋ \left\lfloor\frac{k}{2}\right\rfloor ⌊2k⌋ 个数不可能是第 k k k 小的数,因此我们可以排除数组 n u m s 2 nums2 nums2 的区间 [ j , j + ⌊ k 2 ⌋ ) [j, j + \left\lfloor\frac{k}{2}\right\rfloor) [j,j+⌊2k⌋),递归调用 f ( i , j + ⌊ k 2 ⌋ , k − ⌊ k 2 ⌋ ) f(i, j + \left\lfloor\frac{k}{2}\right\rfloor, k - \left\lfloor\frac{k}{2}\right\rfloor) f(i,j+⌊2k⌋,k−⌊2k⌋)。
时间复杂度 O ( log ( m + n ) ) O(\log(m + n)) O(log(m+n)),空间复杂度 O ( log ( m + n ) ) O(\log(m + n)) O(log(m+n))。其中 m m m 和 n n n 分别是数组 n u m s 1 nums1 nums1 和 n u m s 2 nums2 nums2 的长度。
Python3
python
class Solution:
def findMedianSortedArrays(self, nums1: List[int], nums2: List[int]) -> float:
def f(i: int, j: int, k: int) -> int:
if i >= m:
return nums2[j + k - 1]
if j >= n:
return nums1[i + k - 1]
if k == 1:
return min(nums1[i], nums2[j])
p = k // 2
x = nums1[i + p - 1] if i + p - 1 < m else inf
y = nums2[j + p - 1] if j + p - 1 < n else inf
return f(i + p, j, k - p) if x < y else f(i, j + p, k - p)
m, n = len(nums1), len(nums2)
a = f(0, 0, (m + n + 1) // 2)
b = f(0, 0, (m + n + 2) // 2)
return (a + b) / 2Java
java
class Solution {
private int m;
private int n;
private int[] nums1;
private int[] nums2;
public double findMedianSortedArrays(int[] nums1, int[] nums2) {
m = nums1.length;
n = nums2.length;
this.nums1 = nums1;
this.nums2 = nums2;
int a = f(0, 0, (m + n + 1) / 2);
int b = f(0, 0, (m + n + 2) / 2);
return (a + b) / 2.0;
}
private int f(int i, int j, int k) {
if (i >= m) {
return nums2[j + k - 1];
}
if (j >= n) {
return nums1[i + k - 1];
}
if (k == 1) {
return Math.min(nums1[i], nums2[j]);
}
int p = k / 2;
int x = i + p - 1 < m ? nums1[i + p - 1] : 1 << 30;
int y = j + p - 1 < n ? nums2[j + p - 1] : 1 << 30;
return x < y ? f(i + p, j, k - p) : f(i, j + p, k - p);
}
}C++
cpp
class Solution {
public:
double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) {
int m = nums1.size(), n = nums2.size();
function<int(int, int, int)> f = [&](int i, int j, int k) {
if (i >= m) {
return nums2[j + k - 1];
}
if (j >= n) {
return nums1[i + k - 1];
}
if (k == 1) {
return min(nums1[i], nums2[j]);
}
int p = k / 2;
int x = i + p - 1 < m ? nums1[i + p - 1] : 1 << 30;
int y = j + p - 1 < n ? nums2[j + p - 1] : 1 << 30;
return x < y ? f(i + p, j, k - p) : f(i, j + p, k - p);
};
int a = f(0, 0, (m + n + 1) / 2);
int b = f(0, 0, (m + n + 2) / 2);
return (a + b) / 2.0;
}
};5. 最长回文子串
题目描述
给你一个字符串 s,找到 s 中最长的 回文 子串。
示例 1:
输入: s = "babad"
输出: "bab"
解释:"aba" 同样是符合题意的答案。
示例 2:
输入: s = "cbbd"
输出:"bb"
提示:
1 <= s.length <= 1000s仅由数字和英文字母组成
难度:中等
标签:双指针,字符串,动态规划
解法
方法一:动态规划
我们定义 f [ i ] [ j ] f[i][j] f[i][j] 表示字符串 s [ i . . j ] s[i..j] s[i..j] 是否为回文串,初始时 f [ i ] [ j ] = t r u e f[i][j] = true f[i][j]=true。
接下来,我们定义变量 k k k 和 m x mx mx,其中 k k k 表示最长回文串的起始位置, m x mx mx 表示最长回文串的长度。初始时 k = 0 k = 0 k=0, m x = 1 mx = 1 mx=1。
考虑 f [ i ] [ j ] f[i][j] f[i][j],如果 s [ i ] = s [ j ] s[i] = s[j] s[i]=s[j],那么 f [ i ] [ j ] = f [ i + 1 ] [ j − 1 ] f[i][j] = f[i + 1][j - 1] f[i][j]=f[i+1][j−1];否则 f [ i ] [ j ] = f a l s e f[i][j] = false f[i][j]=false。如果 f [ i ] [ j ] = t r u e f[i][j] = true f[i][j]=true 并且 m x < j − i + 1 mx \lt j - i + 1 mx<j−i+1,那么我们更新 k = i k = i k=i, m x = j − i + 1 mx = j - i + 1 mx=j−i+1。
由于 f [ i ] [ j ] f[i][j] f[i][j] 依赖于 f [ i + 1 ] [ j − 1 ] f[i + 1][j - 1] f[i+1][j−1],因此我们需要保证 i + 1 i + 1 i+1 在 j − 1 j - 1 j−1 之前,因此我们需要从大到小地枚举 i i i,从小到大地枚举 j j j。
时间复杂度 O ( n 2 ) O(n^2) O(n2),空间复杂度 O ( n 2 ) O(n^2) O(n2)。其中 n n n 是字符串 s s s 的长度。
Python3
python
class Solution:
def longestPalindrome(self, s: str) -> str:
n = len(s)
f = [[True] * n for _ in range(n)]
k, mx = 0, 1
for i in range(n - 2, -1, -1):
for j in range(i + 1, n):
f[i][j] = False
if s[i] == s[j]:
f[i][j] = f[i + 1][j - 1]
if f[i][j] and mx < j - i + 1:
k, mx = i, j - i + 1
return s[k : k + mx]Java
java
class Solution {
public String longestPalindrome(String s) {
int n = s.length();
boolean[][] f = new boolean[n][n];
for (var g : f) {
Arrays.fill(g, true);
}
int k = 0, mx = 1;
for (int i = n - 2; i >= 0; --i) {
for (int j = i + 1; j < n; ++j) {
f[i][j] = false;
if (s.charAt(i) == s.charAt(j)) {
f[i][j] = f[i + 1][j - 1];
if (f[i][j] && mx < j - i + 1) {
mx = j - i + 1;
k = i;
}
}
}
}
return s.substring(k, k + mx);
}
}C++
cpp
class Solution {
public:
string longestPalindrome(string s) {
int n = s.size();
vector<vector<bool>> f(n, vector<bool>(n, true));
int k = 0, mx = 1;
for (int i = n - 2; ~i; --i) {
for (int j = i + 1; j < n; ++j) {
f[i][j] = false;
if (s[i] == s[j]) {
f[i][j] = f[i + 1][j - 1];
if (f[i][j] && mx < j - i + 1) {
mx = j - i + 1;
k = i;
}
}
}
}
return s.substr(k, mx);
}
};6. Z 字形变换
题目描述
将一个给定字符串 s 根据给定的行数 numRows ,以从上往下、从左到右进行 Z 字形排列。
比如输入字符串为 "PAYPALISHIRING" 行数为 3 时,排列如下:
P A H N
A P L S I I G
Y I R
之后,你的输出需要从左往右逐行读取,产生出一个新的字符串,比如:"PAHNAPLSIIGYIR"。
请你实现这个将字符串进行指定行数变换的函数:
string convert(string s, int numRows);
示例 1:
输入: s = "PAYPALISHIRING", numRows = 3
输出:"PAHNAPLSIIGYIR"
示例 2:
输入: s = "PAYPALISHIRING", numRows = 4
输出: "PINALSIGYAHRPI"
解释:
P I N
A L S I G
Y A H R
P I
示例 3:
输入: s = "A", numRows = 1
输出:"A"
提示:
1 <= s.length <= 1000s由英文字母(小写和大写)、','和'.'组成1 <= numRows <= 1000
难度:中等
标签:字符串
解法
方法一:模拟
我们用一个二维数组 g g g 来模拟 Z Z Z 字形排列的过程,其中 g [ i ] [ j ] g[i][j] g[i][j] 表示第 i i i 行第 j j j 列的字符。初始时 i = 0 i=0 i=0,另外我们定义一个方向变量 k k k,初始时 k = − 1 k=-1 k=−1,表示向上走。
我们从左到右遍历字符串 s s s,每次遍历到一个字符 c c c,将其追加到 g [ i ] g[i] g[i] 中,如果此时 i = 0 i=0 i=0 或者 i = n u m R o w s − 1 i=numRows-1 i=numRows−1,说明当前字符位于 Z Z Z 字形排列的拐点,我们将 k k k 的值反转,即 k = − k k=-k k=−k。接下来,我们将 i i i 的值更新为 i + k i+k i+k,即向上或向下移动一行。继续遍历下一个字符,直到遍历完字符串 s s s,我们返回 g g g 中所有行拼接后的字符串即可。
时间复杂度 O ( n ) O(n) O(n),空间复杂度 O ( n ) O(n) O(n)。其中 n n n 为字符串 s s s 的长度。
Python3
python
class Solution:
def convert(self, s: str, numRows: int) -> str:
if numRows == 1:
return s
g = [[] for _ in range(numRows)]
i, k = 0, -1
for c in s:
g[i].append(c)
if i == 0 or i == numRows - 1:
k = -k
i += k
return ''.join(chain(*g))Java
java
class Solution {
public String convert(String s, int numRows) {
if (numRows == 1) {
return s;
}
StringBuilder[] g = new StringBuilder[numRows];
Arrays.setAll(g, k -> new StringBuilder());
int i = 0, k = -1;
for (char c : s.toCharArray()) {
g[i].append(c);
if (i == 0 || i == numRows - 1) {
k = -k;
}
i += k;
}
return String.join("", g);
}
}C++
cpp
class Solution {
public:
string convert(string s, int numRows) {
if (numRows == 1) {
return s;
}
vector<string> g(numRows);
int i = 0, k = -1;
for (char c : s) {
g[i] += c;
if (i == 0 || i == numRows - 1) {
k = -k;
}
i += k;
}
string ans;
for (auto& t : g) {
ans += t;
}
return ans;
}
};7. 整数反转
题目描述
给你一个 32 位的有符号整数 x ,返回将 x 中的数字部分反转后的结果。
如果反转后整数超过 32 位的有符号整数的范围 [−231, 231− 1] ,就返回 0。
假设环境不允许存储 64 位整数(有符号或无符号)。
示例 1:
输入: x = 123
**输出:**321
示例 2:
输入: x = -123
输出:-321
示例 3:
输入: x = 120
**输出:**21
示例 4:
输入: x = 0
**输出:**0
提示:
-231<= x <= 231- 1
难度:中等
标签:数学
解法
方法一:数学
我们不妨记 m i mi mi 和 m x mx mx 分别为 − 2 31 -2^{31} −231 和 2 31 − 1 2^{31} - 1 231−1,则 x x x 的反转结果 a n s ans ans 需要满足 m i ≤ a n s ≤ m x mi \le ans \le mx mi≤ans≤mx。
我们可以通过不断地对 x x x 取余来获取 x x x 的最后一位数字 y y y,并将 y y y 添加到 a n s ans ans 的末尾。在添加 y y y 之前,我们需要判断 a n s ans ans 是否溢出。即判断 a n s × 10 + y ans \times 10 + y ans×10+y 是否在 [ m i , m x ] [mi, mx] [mi,mx] 的范围内。
若 x > 0 x \gt 0 x>0,那么需要满足 a n s × 10 + y ≤ m x ans \times 10 + y \leq mx ans×10+y≤mx,即 a n s × 10 + y ≤ ⌊ m x 10 ⌋ × 10 + 7 ans \times 10 + y \leq \left \lfloor \frac{mx}{10} \right \rfloor \times 10 + 7 ans×10+y≤⌊10mx⌋×10+7。整理得 ( a n s − ⌊ m x 10 ⌋ ) × 10 ≤ 7 − y (ans - \left \lfloor \frac{mx}{10} \right \rfloor) \times 10 \leq 7 - y (ans−⌊10mx⌋)×10≤7−y。
下面我们讨论上述不等式成立的条件:
- 当 a n s < ⌊ m x 10 ⌋ ans \lt \left \lfloor \frac{mx}{10} \right \rfloor ans<⌊10mx⌋ 时,不等式显然成立;
- 当 a n s = ⌊ m x 10 ⌋ ans = \left \lfloor \frac{mx}{10} \right \rfloor ans=⌊10mx⌋ 时,不等式成立的充要条件是 y ≤ 7 y \leq 7 y≤7。如果 a n s = ⌊ m x 10 ⌋ ans = \left \lfloor \frac{mx}{10} \right \rfloor ans=⌊10mx⌋ 并且还能继续添加数字,说明此时数字是最高位,即此时 y y y 一定不超过 2 2 2,因此,不等式一定成立;
- 当 a n s > ⌊ m x 10 ⌋ ans \gt \left \lfloor \frac{mx}{10} \right \rfloor ans>⌊10mx⌋ 时,不等式显然不成立。
综上,当 x > 0 x \gt 0 x>0 时,不等式成立的充要条件是 a n s ≤ ⌊ m x 10 ⌋ ans \leq \left \lfloor \frac{mx}{10} \right \rfloor ans≤⌊10mx⌋。
同理,当 x < 0 x \lt 0 x<0 时,不等式成立的充要条件是 a n s ≥ ⌊ m i 10 ⌋ ans \geq \left \lfloor \frac{mi}{10} \right \rfloor ans≥⌊10mi⌋。
因此,我们可以通过判断 a n s ans ans 是否在 [ ⌊ m i 10 ⌋ , ⌊ m x 10 ⌋ ] [\left \lfloor \frac{mi}{10} \right \rfloor, \left \lfloor \frac{mx}{10} \right \rfloor] [⌊10mi⌋,⌊10mx⌋] 的范围内来判断 a n s ans ans 是否溢出。若溢出,则返回 0 0 0。否则,将 y y y 添加到 a n s ans ans 的末尾,然后将 x x x 的最后一位数字去除,即 x ← ⌊ x 10 ⌋ x \gets \left \lfloor \frac{x}{10} \right \rfloor x←⌊10x⌋。
时间复杂度 O ( log ∣ x ∣ ) O(\log |x|) O(log∣x∣),其中 ∣ x ∣ |x| ∣x∣ 为 x x x 的绝对值。空间复杂度 O ( 1 ) O(1) O(1)。
Python3
python
class Solution:
def reverse(self, x: int) -> int:
ans = 0
mi, mx = -(2**31), 2**31 - 1
while x:
if ans < mi // 10 + 1 or ans > mx // 10:
return 0
y = x % 10
if x < 0 and y > 0:
y -= 10
ans = ans * 10 + y
x = (x - y) // 10
return ansJava
java
class Solution {
public int reverse(int x) {
int ans = 0;
for (; x != 0; x /= 10) {
if (ans < Integer.MIN_VALUE / 10 || ans > Integer.MAX_VALUE / 10) {
return 0;
}
ans = ans * 10 + x % 10;
}
return ans;
}
}C++
cpp
class Solution {
public:
int reverse(int x) {
int ans = 0;
for (; x; x /= 10) {
if (ans < INT_MIN / 10 || ans > INT_MAX / 10) {
return 0;
}
ans = ans * 10 + x % 10;
}
return ans;
}
};8. 字符串转换整数 (atoi)
题目描述
请你来实现一个 myAtoi(string s) 函数,使其能将字符串转换成一个 32 位有符号整数。
函数 myAtoi(string s) 的算法如下:
- 空格: 读入字符串并丢弃无用的前导空格(
" ") - 符号: 检查下一个字符(假设还未到字符末尾)为
'-'还是'+'。如果两者都不存在,则假定结果为正。 - **转换:**通过跳过前置零来读取该整数,直到遇到非数字字符或到达字符串的结尾。如果没有读取数字,则结果为0。
- 舍入: 如果整数数超过 32 位有符号整数范围
[−231, 231− 1],需要截断这个整数,使其保持在这个范围内。具体来说,小于−231 的整数应该被舍入为−231 ,大于231− 1的整数应该被舍入为231− 1。
返回整数作为最终结果。
示例 1:
输入: s = "42"
输出: 42
**解释:**加粗的字符串为已经读入的字符,插入符号是当前读取的字符。
带下划线线的字符是所读的内容,插入符号是当前读入位置。
第 1 步:"42"(当前没有读入字符,因为没有前导空格)
^
第 2 步:"42"(当前没有读入字符,因为这里不存在 '-' 或者 '+')
^
第 3 步:"++42++ "(读入 "42")
^
示例 2:
输入: s = " -042"
输出: -42
解释:
第 1 步:"-042"(读入前导空格,但忽视掉)
^
第 2 步:" ++-++ 042"(读入 '-' 字符,所以结果应该是负数)
^
第 3 步:" ++-042++ "(读入 "042",在结果中忽略前导零)
^
示例 3:
输入: s = "1337c0d3"
输出: 1337
解释:
第 1 步:"1337c0d3"(当前没有读入字符,因为没有前导空格)
^
第 2 步:"1337c0d3"(当前没有读入字符,因为这里不存在 '-' 或者 '+')
^
第 3 步:"1337c0d3"(读入 "1337";由于下一个字符不是一个数字,所以读入停止)
^
示例 4:
输入: s = "0-1"
**输出:**0
解释:
第 1 步:"0-1" (当前没有读入字符,因为没有前导空格)
^
第 2 步:"0-1" (当前没有读入字符,因为这里不存在 '-' 或者 '+')
^
第 3 步:"++0++ -1" (读入 "0";由于下一个字符不是一个数字,所以读入停止)
^
示例 5:
输入: s = "words and 987"
输出: 0
解释:
读取在第一个非数字字符"w"处停止。
提示:
0 <= s.length <= 200s由英文字母(大写和小写)、数字(0-9)、' '、'+'、'-'和'.'组成
难度:中等
标签:字符串
解法
方法一:遍历字符串
我们首先判断字符串是否为空,如果是,直接返回 0 0 0。
否则,我们需要遍历字符串,跳过前导空格,判断第一个非空格字符是否为正负号。
接着遍历后面的字符,如果是数字,我们判断添加该数字是否会导致整数溢出,如果会,我们根据正负号返回结果。否则我们将数字添加到结果中。继续遍历后面的字符,直到遇到非数字字符或者遍历结束。
遍历结束后,我们根据正负号返回结果。
时间复杂度 O ( n ) O(n) O(n),其中 n n n 为字符串的长度。我们只需要依次处理所有字符。空间复杂度 O ( 1 ) O(1) O(1)。
Python3
python
class Solution:
def myAtoi(self, s: str) -> int:
if not s:
return 0
n = len(s)
if n == 0:
return 0
i = 0
while s[i] == ' ':
i += 1
# 仅包含空格
if i == n:
return 0
sign = -1 if s[i] == '-' else 1
if s[i] in ['-', '+']:
i += 1
res, flag = 0, (2**31 - 1) // 10
while i < n:
# 非数字,跳出循环体
if not s[i].isdigit():
break
c = int(s[i])
# 溢出判断
if res > flag or (res == flag and c > 7):
return 2**31 - 1 if sign > 0 else -(2**31)
res = res * 10 + c
i += 1
return sign * resJava
java
class Solution {
public int myAtoi(String s) {
if (s == null) return 0;
int n = s.length();
if (n == 0) return 0;
int i = 0;
while (s.charAt(i) == ' ') {
// 仅包含空格
if (++i == n) return 0;
}
int sign = 1;
if (s.charAt(i) == '-') sign = -1;
if (s.charAt(i) == '-' || s.charAt(i) == '+') ++i;
int res = 0, flag = Integer.MAX_VALUE / 10;
for (; i < n; ++i) {
// 非数字,跳出循环体
if (s.charAt(i) < '0' || s.charAt(i) > '9') break;
// 溢出判断
if (res > flag || (res == flag && s.charAt(i) > '7'))
return sign > 0 ? Integer.MAX_VALUE : Integer.MIN_VALUE;
res = res * 10 + (s.charAt(i) - '0');
}
return sign * res;
}
}9. 回文数
题目描述
给你一个整数 x ,如果 x 是一个回文整数,返回 true ;否则,返回 false 。
回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
- 例如,
121是回文,而123不是。
示例 1:
输入: x = 121
**输出:**true
示例 2:
输入: x = -121
输出: false
**解释:**从左向右读, 为 -121 。 从右向左读, 为 121- 。因此它不是一个回文数。
示例 3:
输入: x = 10
输出: false
**解释:**从右向左读, 为 01 。因此它不是一个回文数。
提示:
-231<= x <= 231- 1
**进阶:**你能不将整数转为字符串来解决这个问题吗?
难度:简单
标签:数学
解法
方法一:反转一半数字
我们先判断特殊情况:
- 如果 x < 0 x \lt 0 x<0,那么 x x x 不是回文数,直接返回
false; - 如果 x > 0 x \gt 0 x>0 且 x x x 的个位数是 0 0 0,那么 x x x 不是回文数,直接返回
false; - 如果 x x x 的个位数不是 0 0 0,那么 x x x 可能是回文数,继续执行下面的步骤。
我们将 x x x 的后半部分反转,与前半部分进行比较,如果相等,那么 x x x 是回文数,否则 x x x 不是回文数。
举个例子,例如 x = 1221 x = 1221 x=1221,我们可以将数字后半部分从 "21" 反转为 "12",并将其与前半部分 "12" 进行比较,因为二者相等,我们得知数字 x x x 是回文。
让我们看看如何将后半部分反转。
对于数字 1221 1221 1221,如果执行 1221 m o d 10 1221 \bmod 10 1221mod10,我们将得到最后一位数字 1 1 1,要得到倒数第二位数字,我们可以先通过除以 10 10 10 将最后一位数字从 1221 1221 1221 中移除, 1221 / 10 = 122 1221 / 10 = 122 1221/10=122,再求出上一步结果除以 10 10 10 的余数, 122 m o d 10 = 2 122 \bmod 10 = 2 122mod10=2,就可以得到倒数第二位数字。
如果继续这个过程,我们将得到更多位数的反转数字。
通过将最后一位数字不断地累乘到取出数字的变量 y y y 上,我们可以得到以相反顺序的数字。
在代码实现上,我们可以反复"取出" x x x 的最后一位数字,并将其"添加"到 y y y 的后面,循环直到 y ≥ x y \ge x y≥x,如果此时 x = y x = y x=y,或者 x = y / 10 x = y / 10 x=y/10,那么 x x x 就是回文数。
时间复杂度 O ( log 10 ( n ) ) O(\log_{10}(n)) O(log10(n)),其中 n n n 是 x x x。对于每次迭代,我们会将输入除以 10 10 10,因此时间复杂度为 O ( log 10 ( n ) ) O(\log_{10}(n)) O(log10(n))。空间复杂度 O ( 1 ) O(1) O(1)。
Python3
python
class Solution:
def isPalindrome(self, x: int) -> bool:
if x < 0 or (x and x % 10 == 0):
return False
y = 0
while y < x:
y = y * 10 + x % 10
x //= 10
return x in (y, y // 10)Java
java
class Solution {
public boolean isPalindrome(int x) {
if (x < 0 || (x > 0 && x % 10 == 0)) {
return false;
}
int y = 0;
for (; y < x; x /= 10) {
y = y * 10 + x % 10;
}
return x == y || x == y / 10;
}
}C++
cpp
class Solution {
public:
bool isPalindrome(int x) {
if (x < 0 || (x && x % 10 == 0)) {
return false;
}
int y = 0;
for (; y < x; x /= 10) {
y = y * 10 + x % 10;
}
return x == y || x == y / 10;
}
};10. 正则表达式匹配
题目描述
给你一个字符串 s 和一个字符规律 p,请你来实现一个支持 '.' 和 '*' 的正则表达式匹配。
'.'匹配任意单个字符'*'匹配零个或多个前面的那一个元素
所谓匹配,是要涵盖 整个 字符串 s 的,而不是部分字符串。
示例 1:
输入: s = "aa", p = "a"
输出: false
解释:"a" 无法匹配 "aa" 整个字符串。
示例 2:
输入: s = "aa", p = "a*"
输出: true
**解释:**因为 '*' 代表可以匹配零个或多个前面的那一个元素, 在这里前面的元素就是 'a'。因此,字符串 "aa" 可被视为 'a' 重复了一次。
示例 3:
输入: s = "ab", p = "."
输出: true
解释:"." 表示可匹配零个或多个('*')任意字符('.')。
提示:
1 <= s.length <= 201 <= p.length <= 20s只包含从a-z的小写字母。p只包含从a-z的小写字母,以及字符.和*。- 保证每次出现字符
*时,前面都匹配到有效的字符
难度:困难
标签:递归,字符串,动态规划
解法
方法一:记忆化搜索
我们设计一个函数 d f s ( i , j ) dfs(i, j) dfs(i,j),表示从 s s s 的第 i i i 个字符开始,和 p p p 的第 j j j 个字符开始是否匹配。那么答案就是 d f s ( 0 , 0 ) dfs(0, 0) dfs(0,0)。
函数 d f s ( i , j ) dfs(i, j) dfs(i,j) 的计算过程如下:
- 如果 j j j 已经到达 p p p 的末尾,那么如果 i i i 也到达了 s s s 的末尾,那么匹配成功,否则匹配失败。
- 如果 j j j 的下一个字符是
'*',我们可以选择匹配 0 0 0 个 s [ i ] s[i] s[i] 字符,那么就是 d f s ( i , j + 2 ) dfs(i, j + 2) dfs(i,j+2)。如果此时 i < m i \lt m i<m 并且 s [ i ] s[i] s[i] 和 p [ j ] p[j] p[j] 匹配,那么我们可以选择匹配 1 1 1 个 s [ i ] s[i] s[i] 字符,那么就是 d f s ( i + 1 , j ) dfs(i + 1, j) dfs(i+1,j)。 - 如果 j j j 的下一个字符不是
'*',那么如果 i < m i \lt m i<m 并且 s [ i ] s[i] s[i] 和 p [ j ] p[j] p[j] 匹配,那么就是 d f s ( i + 1 , j + 1 ) dfs(i + 1, j + 1) dfs(i+1,j+1)。否则匹配失败。
过程中,我们可以使用记忆化搜索,避免重复计算。
时间复杂度 O ( m × n ) O(m \times n) O(m×n),空间复杂度 O ( m × n ) O(m \times n) O(m×n)。其中 m m m 和 n n n 分别是 s s s 和 p p p 的长度。
Python3
python
class Solution:
def isMatch(self, s: str, p: str) -> bool:
@cache
def dfs(i, j):
if j >= n:
return i == m
if j + 1 < n and p[j + 1] == '*':
return dfs(i, j + 2) or (
i < m and (s[i] == p[j] or p[j] == '.') and dfs(i + 1, j)
)
return i < m and (s[i] == p[j] or p[j] == '.') and dfs(i + 1, j + 1)
m, n = len(s), len(p)
return dfs(0, 0)Java
java
class Solution {
private Boolean[][] f;
private String s;
private String p;
private int m;
private int n;
public boolean isMatch(String s, String p) {
m = s.length();
n = p.length();
f = new Boolean[m + 1][n + 1];
this.s = s;
this.p = p;
return dfs(0, 0);
}
private boolean dfs(int i, int j) {
if (j >= n) {
return i == m;
}
if (f[i][j] != null) {
return f[i][j];
}
boolean res = false;
if (j + 1 < n && p.charAt(j + 1) == '*') {
res = dfs(i, j + 2)
|| (i < m && (s.charAt(i) == p.charAt(j) || p.charAt(j) == '.') && dfs(i + 1, j));
} else {
res = i < m && (s.charAt(i) == p.charAt(j) || p.charAt(j) == '.') && dfs(i + 1, j + 1);
}
return f[i][j] = res;
}
}C++
cpp
class Solution {
public:
bool isMatch(string s, string p) {
int m = s.size(), n = p.size();
int f[m + 1][n + 1];
memset(f, 0, sizeof f);
function<bool(int, int)> dfs = [&](int i, int j) -> bool {
if (j >= n) {
return i == m;
}
if (f[i][j]) {
return f[i][j] == 1;
}
int res = -1;
if (j + 1 < n && p[j + 1] == '*') {
if (dfs(i, j + 2) or (i < m and (s[i] == p[j] or p[j] == '.') and dfs(i + 1, j))) {
res = 1;
}
} else if (i < m and (s[i] == p[j] or p[j] == '.') and dfs(i + 1, j + 1)) {
res = 1;
}
f[i][j] = res;
return res == 1;
};
return dfs(0, 0);
}
};