详解残差网络
ResNets 是由残差块(Residual block)构建的,首先解释一下什么是残差块。
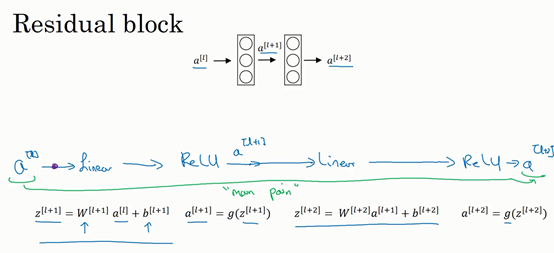
这是一个两层神经网络,在\(L\)层进行激活,得到\(a^{\left\lbrack l + 1 \right\rbrack}\),再次进行激活,两层之后得到\(a^{\left\lbrack l + 2 \right\rbrack}\)。计算过程是从\(a^{[l]}\)开始,首先进行线性激活,根据这个公式:\(z^{\left\lbrack l + 1 \right\rbrack} = W^{\left\lbrack l + 1 \right\rbrack}a^{[l]} + b^{\left\lbrack l + 1 \right\rbrack}\),通过\(a^{[l]}\)算出\(z^{\left\lbrack l + 1 \right\rbrack}\),即\(a^{[l]}\)乘以权重矩阵,再加上偏差因子。然后通过ReLU 非线性激活函数得到\(a^{\left\lbrack l + 1 \right\rbrack}\),\(a^{\left\lbrack l + 1 \right\rbrack} =g(z^{\left\lbrack l + 1 \right\rbrack})\)计算得出。接着再次进行线性激活,依据等式\(z^{\left\lbrack l + 2 \right\rbrack} = W^{\left\lbrack 2 + 1 \right\rbrack}a^{\left\lbrack l + 1 \right\rbrack} + b^{\left\lbrack l + 2 \right\rbrack}\),最后根据这个等式再次进行ReLu 非线性激活,即\(a^{\left\lbrack l + 2 \right\rbrack} = g(z^{\left\lbrack l + 2 \right\rbrack})\),这里的\(g\)是指ReLU 非线性函数,得到的结果就是\(a^{\left\lbrack l + 2 \right\rbrack}\)。换句话说,信息流从\(a^{\left\lbrack l \right\rbrack}\)到\(a^{\left\lbrack l + 2 \right\rbrack}\)需要经过以上所有步骤,即这组网络层的主路径。
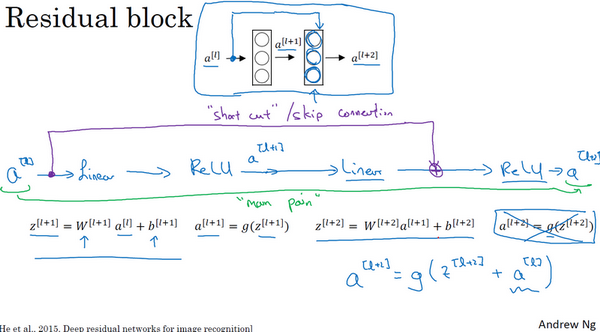
在残差网络中有一点变化,将\(a^{[l]}\)直接向后,拷贝到神经网络的深层,在ReLU 非线性激活函数前加上\(a^{[l]}\),这是一条捷径。\(a^{[l]}\)的信息直接到达神经网络的深层,不再沿着主路径传递,这就意味着最后这个等式(\(a^{\left\lbrack l + 2 \right\rbrack} = g(z^{\left\lbrack l + 2 \right\rbrack})\))去掉了,取而代之的是另一个ReLU 非线性函数,仍然对\(z^{\left\lbrack l + 2 \right\rbrack}\)进行\(g\)函数处理,但这次要加上\(a^{[l]}\),即:\(\ a^{\left\lbrack l + 2 \right\rbrack} = g\left(z^{\left\lbrack l + 2 \right\rbrack} + a^{[l]}\right)\),也就是加上的这个\(a^{[l]}\)产生了一个残差块。
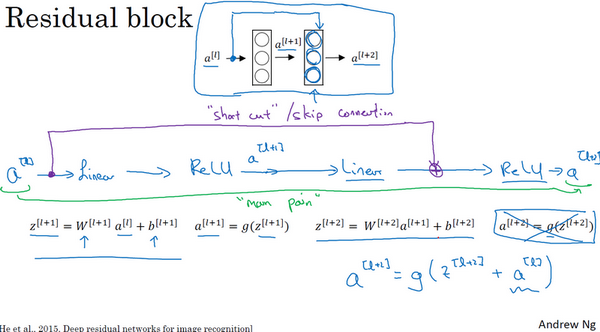
在上面这个图中,也可以画一条捷径,直达第二层。实际上这条捷径是在进行ReLU 非线性激活函数之前加上的,而这里的每一个节点都执行了线性函数和ReLU 激活函数。所以\(a^{[l]}\)插入的时机是在线性激活之后,ReLU 激活之前。除了捷径,还会听到另一个术语"跳跃连接",就是指\(a^{[l]}\)跳过一层或者好几层,从而将信息传递到神经网络的更深层。
ResNet 的发明者是何凯明 (Kaiming He )、张翔宇 (Xiangyu Zhang )、任少卿 (Shaoqing Ren )和孙剑 (Jiangxi Sun ),他们发现使用残差块能够训练更深的神经网络。所以构建一个ResNet网络就是通过将很多这样的残差块堆积在一起,形成一个很深神经网络,来看看这个网络。

这并不是一个残差网络,而是一个普通网络(Plain network ),这个术语来自ResNet论文。
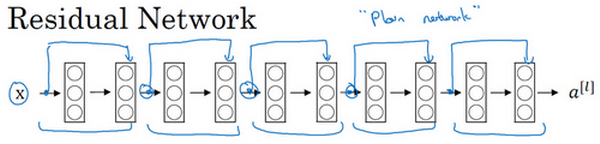
把它变成ResNet的方法是加上所有跳跃连接,每两层增加一个捷径,构成一个残差块。如图所示,5个残差块连接在一起构成一个残差网络。
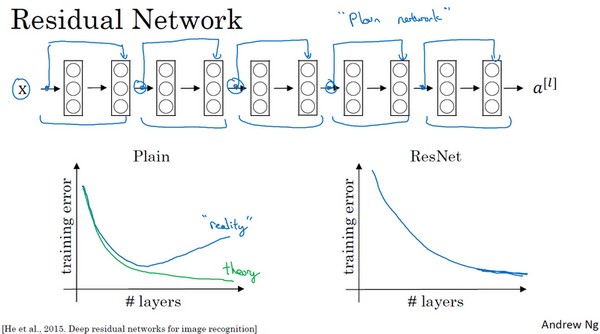
如果使用标准优化算法训练一个普通网络,比如说梯度下降法,或者其它热门的优化算法。如果没有残差,没有这些捷径或者跳跃连接,凭经验会发现随着网络深度的加深,训练错误会先减少,然后增多。而理论上,随着网络深度的加深,应该训练得越来越好才对。也就是说,理论上网络深度越深越好。但实际上,如果没有残差网络,对于一个普通网络来说,深度越深意味着用优化算法越难训练。实际上,随着网络深度的加深,训练错误会越来越多。
但有了ResNets 就不一样了,即使网络再深,训练的表现却不错,比如说训练误差减少,就算是训练深达100层的网络也不例外。有人甚至在1000多层的神经网络中做过实验,尽管目前还没有看到太多实际应用。但是对\(x\)的激活,或者这些中间的激活能够到达网络的更深层。这种方式确实有助于解决梯度消失和梯度爆炸问题,让在训练更深网络的同时,又能保证良好的性能。也许从另外一个角度来看,随着网络越来深,网络连接会变得臃肿,但是ResNet确实在训练深度网络方面非常有效。