七战字节
今天逛牛客网的时候,又看到一篇《伤心字节》系列帖子:
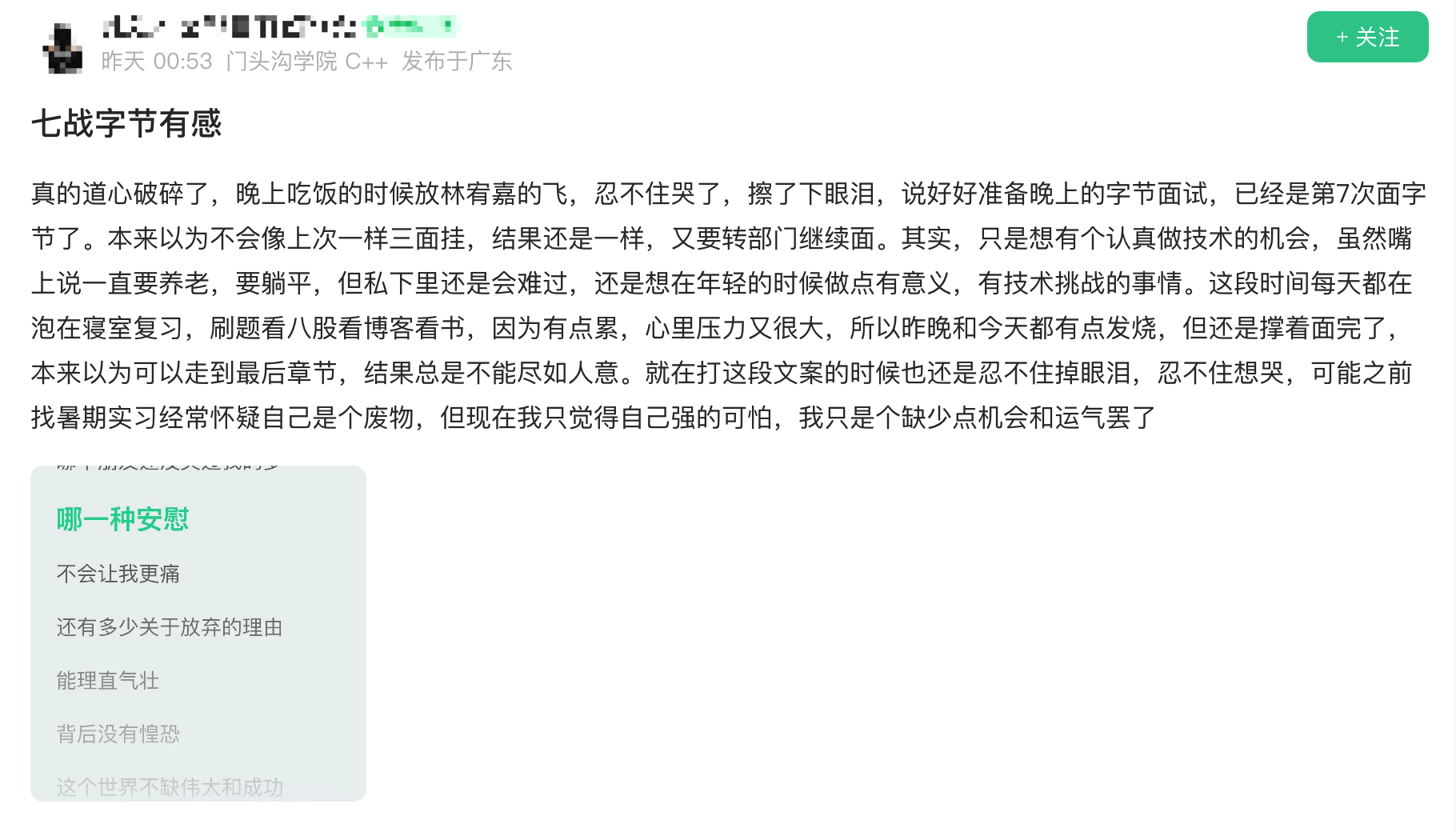
这位同事说道,面字节已经面到道心破碎,吃饭的时候听林宥嘉更是直接泪崩。
这已经是贴主的第 7 次面字节,而且这次和上次一样,都是三面挂,只能转部门继续面。
楼主直言道:虽然平日嘴上一直说想养老想躺平,但还是想趁年轻做一些有意义,有技术挑战的事情。
这段时间每天都泡在宿舍准备面试,心理压力很大,甚至都已经熬到有点发烧了,但还是硬撑着面完了,但结果还是不如人意。
言语间,真的很心疼这届应届生。
往下翻了一下评论区,发现这个世界真的「没有最惨,只有更惨」。
一位同学表示,自己已经面了字节 13 次了,而且还在坚持面。
另外其他同学也表示自己正在艰难秋招,与楼主相互加油。
从结果来看,字节是一个庞大的体系(市值全球第一的独角兽),里面的部门组织更是高度复杂,因此七面、十面的人大有人在。对于此类企业,我们能做到的就是全力准备,认真复盘,然后平常心面对。只要面试过程不犯原则性错误(笔试作弊、与面试官产生冲突),基本上这次挂了,不会影响下个部门邀面。
...
回归主题。
来一道热门社招算法题。
题目描述
平台:LeetCode
题号:面试题 03.01. 三合一
三合一。
描述如何只用一个数组来实现三个栈。
你应该实现 push(stackNum, value)、pop(stackNum)、isEmpty(stackNum)、peek(stackNum) 方法。
stackNum 表示栈下标,value 表示压入的值。
构造函数会传入一个 stackSize 参数,代表每个栈的大小。
示例1:
输入:
["TripleInOne", "push", "push", "pop", "pop", "pop", "isEmpty"]
[[1], [0, 1], [0, 2], [0], [0], [0], [0]]
输出:
[null, null, null, 1, -1, -1, true]
说明:当栈为空时`pop, peek`返回-1,当栈满时`push`不压入元素。示例2:
输入:
["TripleInOne", "push", "push", "push", "pop", "pop", "pop", "peek"]
[[2], [0, 1], [0, 2], [0, 3], [0], [0], [0], [0]]
输出:
[null, null, null, null, 2, 1, -1, -1]二维数组
题目只要求我们使用「一个数组」来实现栈,并没有限制我们使用数组的维度。
因此一个简单的做法是,建立一个二维数组 data 来做。
二维数组的每一行代表一个栈,同时使用一个 locations 记录每个栈「待插入」的下标。
代码:
class TripleInOne {
int N = 3;
// 3 * n 的数组,每一行代表一个栈
int[][] data;
// 记录每个栈「待插入」位置
int[] locations;
public TripleInOne(int stackSize) {
data = new int[N][stackSize];
locations = new int[N];
}
public void push(int stackNum, int value) {
int[] stk = data[stackNum];
int loc = locations[stackNum];
if (loc < stk.length) {
stk[loc] = value;
locations[stackNum]++;
}
}
public int pop(int stackNum) {
int[] stk = data[stackNum];
int loc = locations[stackNum];
if (loc > 0) {
int val = stk[loc - 1];
locations[stackNum]--;
return val;
} else {
return -1;
}
}
public int peek(int stackNum) {
int[] stk = data[stackNum];
int loc = locations[stackNum];
if (loc > 0) return stk[loc - 1];
else return -1;
}
public boolean isEmpty(int stackNum) {
return locations[stackNum] == 0;
}
}C++ 代码:
class TripleInOne {
public:
int N = 3;
vector<vector<int>> data;
vector<int> locations;
TripleInOne(int stackSize) {
data.resize(N, vector<int>(stackSize));
locations.resize(N, 0);
}
void push(int stackNum, int value) {
vector<int>& stk = data[stackNum];
int loc = locations[stackNum];
if (loc < stk.size()) {
stk[loc] = value;
locations[stackNum]++;
}
}
int pop(int stackNum) {
vector<int>& stk = data[stackNum];
int loc = locations[stackNum];
if (loc > 0) {
int val = stk[--loc];
locations[stackNum] = loc;
return val;
} else {
return -1;
}
}
int peek(int stackNum) {
vector<int>& stk = data[stackNum];
int loc = locations[stackNum];
if (loc > 0) return stk[loc - 1];
else return -1;
}
bool isEmpty(int stackNum) {
return locations[stackNum] == 0;
}
};- 时间复杂度:所有的操作均为 。
- 空间复杂度: 。 为我们需要实现的栈的个数, 为栈的容量。
一维数组
当然了,我们也能使用一个一维数组来做。
建立一个长度为 的数组,并将 3 个栈的「待插入」存储在 locations 数组。
代码:
class TripleInOne {
int N = 3;
int[] data, locations;
int size;
public TripleInOne(int stackSize) {
size = stackSize;
data = new int[size * N];
locations = new int[N];
for (int i = 0; i < N; i++) locations[i] = i * size;
}
public void push(int stackNum, int value) {
int idx = locations[stackNum];
if (idx < (stackNum + 1) * size) {
data[idx] = value;
locations[stackNum]++;
}
}
public int pop(int stackNum) {
int idx = locations[stackNum];
if (idx > stackNum * size) {
locations[stackNum]--;
return data[idx - 1];
} else {
return -1;
}
}
public int peek(int stackNum) {
int idx = locations[stackNum];
if (idx > stackNum * size) return data[idx - 1];
else return -1;
}
public boolean isEmpty(int stackNum) {
return locations[stackNum] == stackNum * size;
}
}C++ 代码:
class TripleInOne {
public:
int N = 3;
vector<int> data, locations;
int size;
TripleInOne(int stackSize) : size(stackSize), data(stackSize * N), locations(N, 0) {
for (int i = 0; i < N; i++) locations[i] = i * size;
}
void push(int stackNum, int value) {
int idx = locations[stackNum];
if (idx < (stackNum + 1) * size) {
data[idx] = value;
locations[stackNum]++;
}
}
int pop(int stackNum) {
int idx = locations[stackNum];
if (idx > stackNum * size) {
locations[stackNum]--;
return data[idx - 1];
} else {
return -1;
}
}
int peek(int stackNum) {
int idx = locations[stackNum];
if (idx > stackNum * size) return data[idx - 1];
else return -1;
}
bool isEmpty(int stackNum) {
return locations[stackNum] == stackNum * size;
}
};- 时间复杂度:所有的操作均为 。
- 空间复杂度: 。 为我们需要实现的栈的个数, 为栈的容量。
最后
巨划算的 LeetCode 会员优惠通道目前仍可用 ~
使用福利优惠通道 leetcode.cn/premium/?promoChannel=acoier ,年度会员 有效期额外增加两个月 ,季度会员 有效期额外增加两周,更有超大额专属 🧧 和实物 🎁 福利每月发放。
我是宫水三叶,每天都会分享算法知识 ,并和大家聊聊近期的所见所闻。
欢迎关注,明天见。
更多更全更热门的「笔试/面试」相关资料可访问排版精美的 合集新基地 🎉🎉