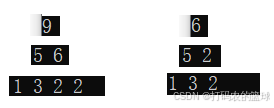每日回顾：简单用C搓个数组堆

heap.h------标准库包含、函数声明

heap.c------函数定义

main.c------测试

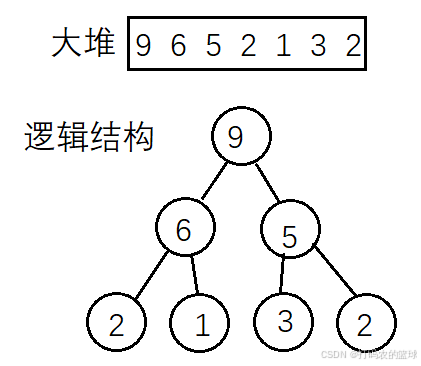
堆的逻辑结构是一颗完全二叉树：

heap.h

heap.h中应包含如下定义和功能：

cpp 复制代码

#pragma once
#include<stdio.h>
#include<stdbool.h>
#include<assert.h>
#include<stdlib.h>

typedef int HPDataType;
typedef struct Heap
{
	HPDataType* a;
	int size;
	int capacity;
}Heap;

// 堆初始化
void HeapInit(Heap* php);
// 堆的销毁
void HeapDestory(Heap* hp);

//向上调整
void AdjustUp(HPDataType* a, int child);
// 堆的插入
void HeapPush(Heap* hp, HPDataType x);

//向下调整
void AdjustDown(HPDataType* a, int n, int parent);
// 堆的删除（删除堆顶元素）
void HeapPop(Heap* hp);

// 取堆顶的数据
HPDataType HeapTop(Heap* hp);
// 堆的数据个数
int HeapSize(Heap* hp);
// 堆的判空
bool HeapEmpty(Heap* hp);

heap.c

逐个在 heap.c 中实现上述功能，同时保证代码的健壮性：

在 heap.c 中包含 heap.h

1、堆初始化

cpp 复制代码

// 堆初始化
void HeapInit(Heap* php) {
	assert(php);
	php->a = NULL;
	php->capacity = 0;
	php->size = 0;
}

2、堆的销毁

cpp 复制代码

// 堆的销毁
void HeapDestory(Heap* hp) {
	assert(hp);
	free(hp->a);
}

3、向上调整

cpp 复制代码

//交换元素
void Swap(HPDataType* p1, HPDataType* p2) {
	HPDataType tmp = *p1;
	*p1 = *p2;
	*p2 = tmp;
}

//向上调整
void AdjustUp(HPDataType* a, int child) {
	int parent = (child - 1) / 2;
	//只要 child 有效，都会进入循环判断
	while (child > 0) {
		//建立大堆
		if (a[child] > a[parent]) {
			Swap(&a[child], &a[parent]);
			child = parent;
			parent = (child - 1) / 2;
		}
		else {	//已满足堆的条件
			break;
		}
	}
}

4、堆的插入

cpp 复制代码

// 堆的插入
void HeapPush(Heap* hp, HPDataType x) {
	assert(hp);
	//检查容量，如果已满，扩容
	if (hp->size == hp->capacity) {
		int newCapacity = hp->capacity == 0 ? 4 : hp->capacity * 2;
		HPDataType* tmp = (HPDataType*)realloc(hp->a, sizeof(HPDataType) * newCapacity);
		if (tmp == NULL) {
			perror("realloc failed");
			return;
		}
		hp->a = tmp;
		hp->capacity = newCapacity;
	}

	hp->a[hp->size++] = x;
	//尾插新数据后，向上调整
	//传入数组和孩子下标
	AdjustUp(hp->a, hp->size - 1);
}

5、向下调整

cpp 复制代码

//向下调整
void AdjustDown(HPDataType* a, int n, int parent) {
	int child = parent * 2 + 1;	//左孩子
	//调整时，parent 要与 左右孩子中大的那个交换--
	//--以保证满足大堆条件

	while (child < n) {
		//选出左右孩子中较大者
		if ((child + 1) < n && a[child] < a[child + 1]) {
			child++;
		}

		if (a[parent] < a[child]) {
			Swap(&a[parent], &a[child]);
			parent = child;
			child = parent * 2 + 1;
		}
		else {	//已满足大堆条件
			break;
		}
	}
}

6、堆的删除

cpp 复制代码

// 堆的删除（删除堆顶元素）
void HeapPop(Heap* hp) {
	//交换堆顶和堆底元素，删除堆底元素，向下调整
	assert(hp);
	assert(!HeapEmpty(hp));	//堆不能为空

	Swap(&hp->a[0], &hp->a[hp->size - 1]);
	hp->size--;
	AdjustDown(hp->a, hp->size, 0);
}

7、取堆顶元素

cpp 复制代码

// 取堆顶的数据
HPDataType HeapTop(Heap* hp) {
	assert(hp);
	assert(!HeapEmpty(hp));	//堆不能为空
	return hp->a[0];
}

8、堆的数据个数

cpp 复制代码

// 堆的数据个数
int HeapSize(Heap* hp) {
	assert(hp);
	return hp->size;
}

9、判断堆空

cpp 复制代码

// 堆的判空
bool HeapEmpty(Heap* hp) {
	assert(hp);
	return hp->size == 0;
}

main.c

cpp 复制代码

#include"heap.h"

void Test1() {
	Heap hp;
	HeapInit(&hp);

	HeapPush(&hp, 2);
	HeapPush(&hp, 1);
	HeapPush(&hp, 3);
	HeapPush(&hp, 6);
	HeapPush(&hp, 5);
	HeapPush(&hp, 9);
	HeapPush(&hp, 2);

	for (int i = 0; i < hp.size; i++) {
		printf("%d ", hp.a[i]);
	}
	printf("\n");

	HeapPop(&hp);
	for (int i = 0; i < hp.size; i++) {
		printf("%d ", hp.a[i]);
	}

	HeapDestory(&hp);
}

int main() {
	Test1();
	return 0;
}

将存储的数据拆成完全二叉树后，仍然是大堆，没有问题