利用Matlab工具生成滤波器
简介
利用Matlab生成IIR型滤波器,IIR型会引入输出项,重新计算出新的输出项;使用matlab的滤波器设计工具,得到系数 a , b a,b a,b,再利用推导出来的公式,带入即可;
Matlab生成系数
以低通滤波器为例:
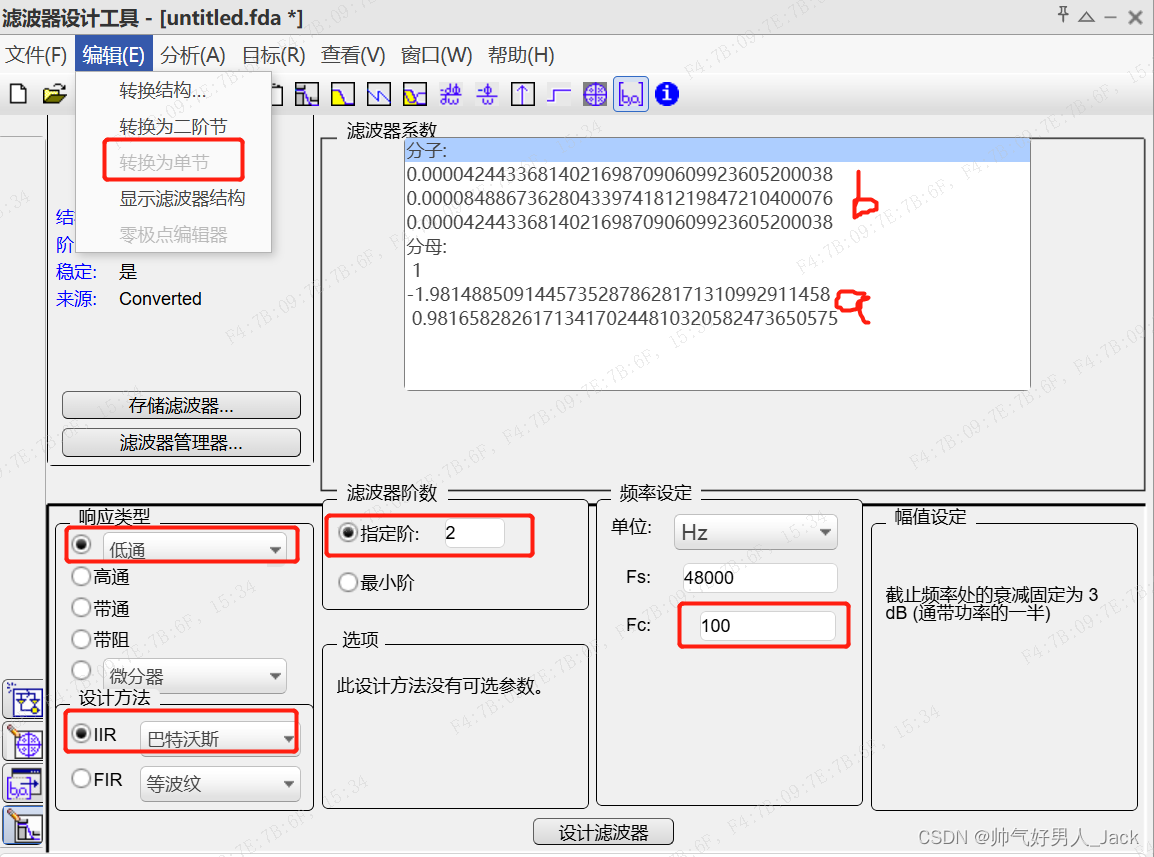
- F c F_c Fc截止频率,也就是说从通带开始到截止频率处,dB值会下降3dB
- F s F_s Fs采样率,采样率要尽可能大一点,过小会造成频谱泄露
- 指定的阶数这里取2,就是参数 a a a会使用到2个
使用IIR型的巴特沃斯函数来构造的参数,其函数图像如下:
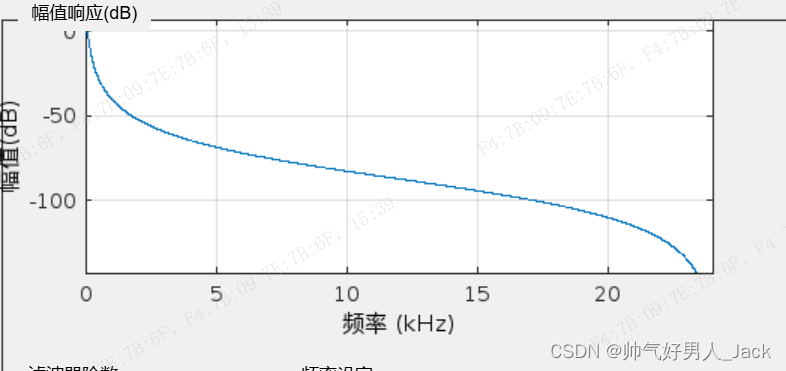
函数图如上,随着频率的上升,dB值呈单调递减的效果,也就是最后经过我们处理后的音频数据也会呈现这种效果;
从上面我们就拿到了 a , b a,b a,b系数,带入下面公式即可
低通滤波器公式
引入IIR型推导出的2阶公式,此公式由前人推导而出,推导相对复杂,后面会有文章简单讲解:
y ( n ) = b 0 ∗ x ( n ) + b 1 ∗ x ( n − 1 ) + b 2 ∗ x ( n − 2 ) − a 1 ∗ y ( n − 1 ) − a 2 ∗ y ( n − 2 ) y(n) = b_0*x(n) + b_1*x(n-1) + b_2*x(n-2) - a_1*y(n-1) - a_2*y(n-2) y(n)=b0∗x(n)+b1∗x(n−1)+b2∗x(n−2)−a1∗y(n−1)−a2∗y(n−2)
最后,将待处理的数据带入公式接口,大致算法如下:
python
for index in range(len(data)):
if index < 2:
low_signal[index] = data[index]
continue
low_signal[index] = b_p[0] * data[index] + b_p[1] * data[index-1] + b_p[2] * data[index-2] - a_p[1] * low_signal[index-1] - a_p[2]*low_signal[index-2]最后运行的效果如下:
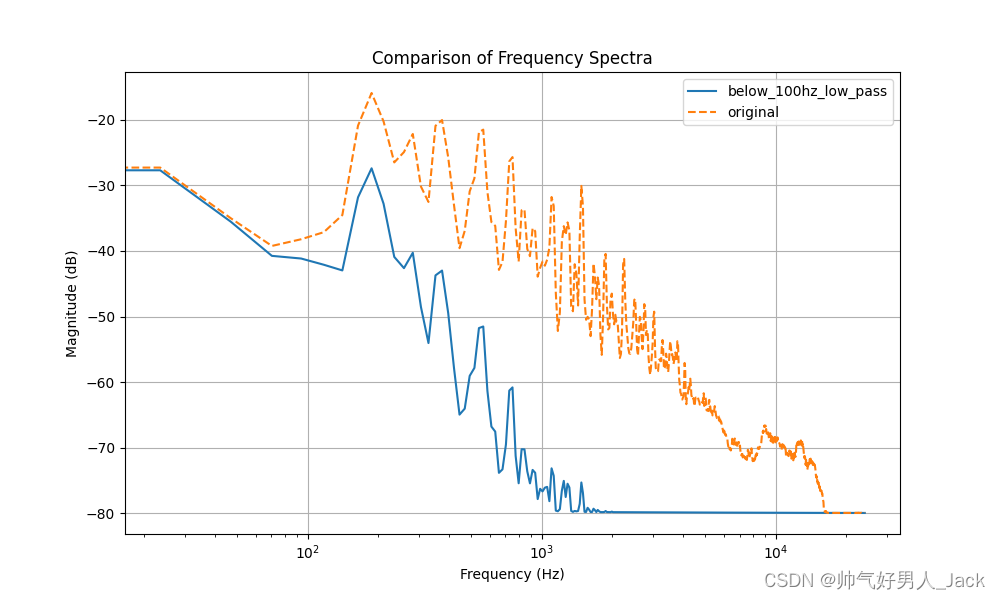
其它的高通滤波器、带通和带阻滤波器也可以按照这种方法做,是不是很简单;还是要理解好原理才重要;