两道算法题 - 技术栈

一、算法一

Amazon would like to enforce a password policy that when a user changes their password, the new password cannot be similar to the current one. To determine whether two passwords are similar, they take the new password, choose a set of indices and change the characters at these indices to the next cyclic character exactly once. Character 'a' is changed to 'b', 'b' to 'c' and so on, and 'z' changes to 'a'.The password is said to be similar if after applying the operation, the old password is a subsequence of the new password. The developers come up with a set of n password change requests, where newPasswords denotes the array of new passwords and oldPasswords denotes the array of old passwords. For each pair newPasswords $i$ and oldPasswords $i$ , return "YES" if the passwords are similar, that is, newPasswords $i$ becomes a subsequence of oldPasswords $i$ after performing the operations, and "No" otherwise. Note: A subsequence is a sequence that can be derived from the given sequence by deleting zero or more elements without changing the order of the remaining elements.

Example: the two lists of passwords are given as newPasswords = $"baacbab", "accdb", "baacba"$ , and oldPasswords = $"abdbc", "ach","abb"$ .

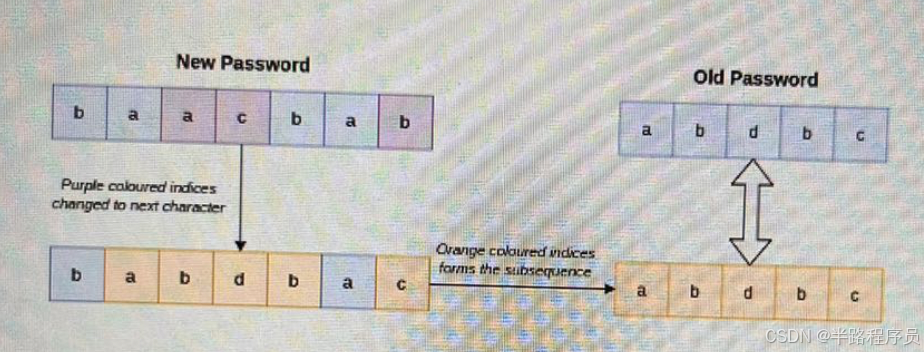
Consider the first pair: newPasswords $0$ = "baacbab"and oldPasswords ="abdbc". Change "ac to "bd"at the 3rd and 4th positions, and "b"to "c" at the last position. The answer for this pair is YES.

The newPasswords $1$ = "accdb" and oldPasswords = "ach". It is not possible to change the character of the new password to "h" which occurs in the old password, so there is no subsequence that matches. The answer for this pair is NO.

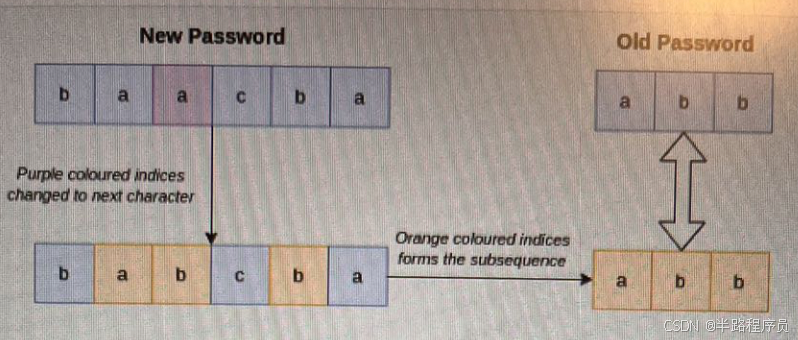
newPasswords $2$ = "baacba" and oldPasswords = "abb". The answer for this pair is YES.

Return $"YES", "NO", YES"$ .

Function Description complete the function findSimilarities below.

findSimilarities has the following parameters:

string newPasswords $n$ : newPasswords $i$ represents the new password of the i-th pair
string oldPasswords $n$ : oldPasswords $i$ represents the old password of the i-th pair

returns

string $n$ : the i-th string represents the answer to the i-th pair of passwords

constraints:

1、1 <= n <= 10
2、Sum of lengths of all passwords in array newPassword and array oldPassword does not exceed(2*10^5)
3、|oldPasswords $i$ | <= |newPasswords $i$ |, for all i

算法思路是：遍历每一对oldPasswords $i$ 和newPasswords $i$ ，判断经过上述的变换之后，oldPasswords $i$ 是否可以成为newPasswords $i$ 的子序列，注意这里是序列，而不是子串，由于题目中说了对newPasswords $i$ 的变换可以不是全部字符，而可以是部分字符，所以思路就是用双指针i,j，i指向newPasswords $k$ 的起始位置，j指向oldPasswords $k$ 的起始位置，然后依次向后遍历，每走一个位置判断newPassword. charAt(i) == oldPassword. charAt(j) 或者nextCyclicChar(newPassword.charAt(i))== oldPassword.charAt(j)，条件满足则j++，i不论满不满足都执行加一操作，最后判断是否完整遍历了oldPassword，也就是返回时判断j==j oldPassword.length()是否成立。下面是java代码：

二、算法二

An Amazon fulfillment center receives a large number of orders each day. Each order is associated with a range of prices of items that need to be picked from the warehouse and packed into a box. There are n items in the warehouse, which are represented as an array items $n$ . The value of items $i$ represents the value of i-th item in the warehouse, and subsequently there are m orders. The start_index and end_ index for the i-th order are represented in the arrays start $i$ and end $i$ . Also start $i$ and end $i$ are 0-index based.

For each order, all the items are picked from the inclusive range from start $i$ through end $i$ . Given array items, start, end, and query. For each query $i$ , find the count of elements in the range with a value strictly less than query $i$ .

Example:

Given, n = 5, items = $1, 2, 5, 4, 5$ , m = 3, start = $0, 0, 1$ , end = $1, 2, 2$ and query= $2, 4$ .

order Number	start index	end index	picked items
1st	0	1	$1, 2$
2nd	0	2	$1, 2, 5$
3rd	1	2	$2, 5$

over the 3 orders, the picked items are $1, 2, 1, 2, 5, 2, 5$ .

For the first query, 2 picked items have values less than 2. 5 picked items have values less than 4. Hence the answer is $2, 5$ .

Function Description: Complete the function getSmalleritems below.

getSmalleritems has the following parameter(s):

int items $n$ : the value of each item
int start $m$ : the start index for each order
int end $m$ :the end index for each order
int query $q$ : query values

Returns: long output $q$ : the answer for each query, the number of picked items having a value strictly less than query $i$ .

Constraints:

1≤ n ≤ 10^5
1 ≤ items $i$ ≤ 10^9, where 0 ≤ i < n
0 ≤ m ≤ 10^5
0 ≤ start $i$ ≤ end $i$ < n, where 0 ≤ i < m
1 ≤ q ≤ 10^5
1 ≤ query $i$ ≤ 10^9，where 0 ≤ i < q

python 复制代码

from typing import List
from collections import defaultdict

def getSmalleritems(items: List[int], start: List[int], end: List[int], query: List[int]) -> List[int]:
    # 创建一个字典来存储每个值的出现次数
    value_count = defaultdict(int)
    
    # 遍历所有订单，统计每个值的出现次数
    for i in range(len(start)):
        for j in range(start[i], end[i] + 1):
            value_count[items[j]] += 1
    
    # 对值进行排序
    sorted_values = sorted(value_count.keys())
    
    # 计算前缀和
    prefix_sum = [0]
    for value in sorted_values:
        prefix_sum.append(prefix_sum[-1] + value_count[value])
    
    # 处理查询
    result = []
    for q in query:
        # 使用二分查找找到小于q的最大值的索引
        left, right = 0, len(sorted_values)
        while left < right:
            mid = (left + right) // 2
            if sorted_values[mid] < q:
                left = mid + 1
            else:
                right = mid
        
        # 返回前缀和
        result.append(prefix_sum[left])
    
    return result

# 测试代码
# items = [1, 2, 5, 4, 5]
# start = [0, 0, 1]
# end = [1, 2, 2]
# query = [2, 4]
# output = [2, 5]

# items = [1, 2, 3, 2, 4, 1]
# start = [2, 0]
# end = [4, 0]
# query = [5, 3]
# output = [4, 2]

items = [4, 4, 5, 3, 2]
start = [0, 1, 0, 2]
end = [1, 2, 3, 4]
query = [5, 4, 1]
# output = [8, 3, 0]

print(getSmalleritems(items, start, end, query))