
摘要
本文研究了无人机设计与控制中的几种经典控制方法,包括PID控制、反步法和滑模控制,旨在实现四旋翼无人机的轨迹跟踪控制。通过Matlab仿真实验,对比分析了各方法在轨迹跟踪中的性能表现。
结果表明,各种方法均能实现基本的轨迹跟踪,其中滑模控制在对抗扰动和跟踪精度方面具有显著优势。
理论
1. PID控制理论
PID控制是一种经典的控制方法,其核心是通过比例、积分和微分控制器对系统的误差进行修正。PID控制适用于线性和部分非线性系统,具有结构简单、易于实现的特点。
控制律如下:
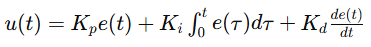
2. 反步法控制理论
反步法是一种基于Lyapunov稳定性理论的非线性控制设计方法。通过逐步设计虚拟控制变量,反步法逐步构造控制律,从而保证系统的全局稳定性。
对于四旋翼无人机模型,反步法的核心是将系统的非线性项逐步引入,并通过Lyapunov函数设计每步的控制输入。
3. 滑模控制理论
滑模控制是一种鲁棒性很强的非线性控制方法。通过设计切换函数和滑模面,滑模控制可以在系统存在不确定性或外界扰动时,保证系统的动态性能。
滑模控制律如下:
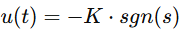
其中,滑模面𝑠=𝑒+𝜆𝑒。
实验结果
实验分别针对PID控制、反步法和滑模控制进行了四旋翼无人机的轨迹跟踪仿真。以下是关键实验结果:
-
PID控制仿真:PID控制能够实现基本的轨迹跟踪,但在系统受到扰动时性能下降。
-
反步法控制仿真:反步法能够较好地应对非线性动态,跟踪精度高。
-
滑模控制仿真:滑模控制表现出较强的鲁棒性,对扰动具有较强的抗干扰能力。
实验数据和对比图表如下图所示:
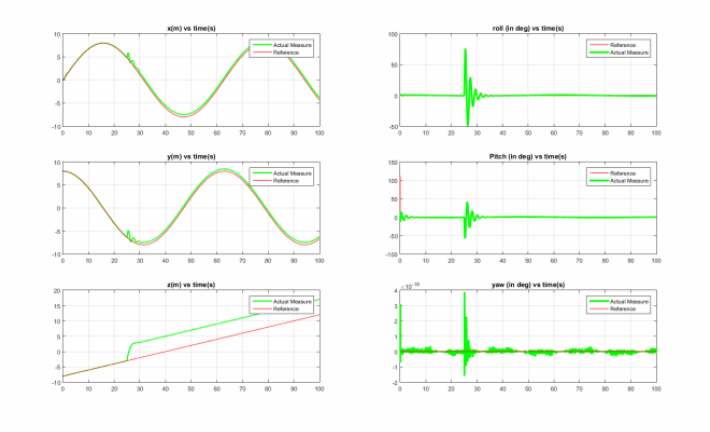
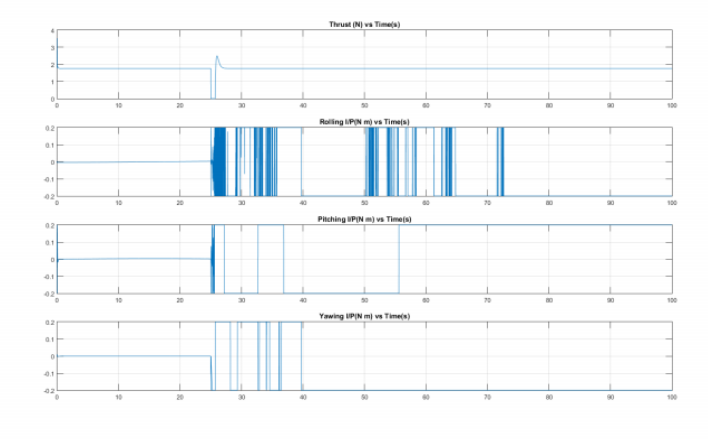
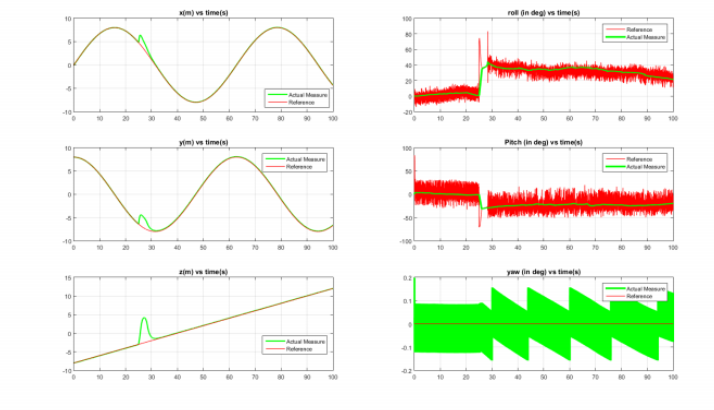
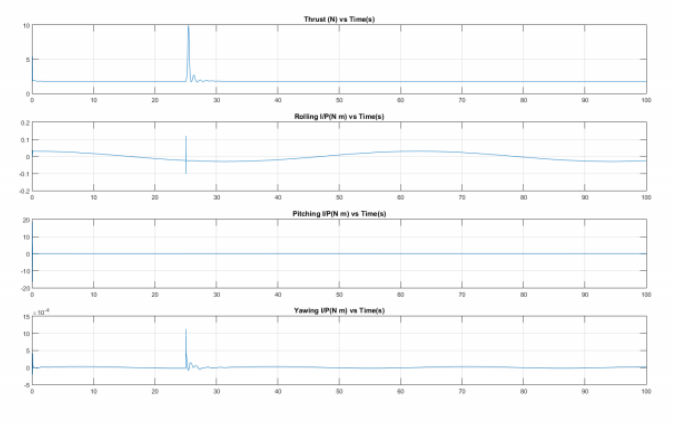
部分代码
% PID控制代码
Kp = 1; Ki = 0.5; Kd = 0.1;
setpoint = desired_trajectory; % 设定轨迹
error = setpoint - actual_position;
for t = 1:length(time)
integral = integral + error(t)*dt;
derivative = (error(t) - error(t-1))/dt;
control_input = Kp*error(t) + Ki*integral + Kd*derivative;
% 更新无人机状态
end
% 反步法控制
function u = backstepping_control(x, x_desired)
% Lyapunov函数设计
e = x - x_desired;
u = -K1 * e - K2 * dot(e);
end
% 滑模控制
function u = sliding_mode_control(s)
u = -K * sign(s); % 控制输入
end参考文献
❝
Zhang, Y., & Du, W. (2018). Adaptive Sliding Mode Control for Quadrotor UAVs with External Disturbance. International Journal of Control, Automation and Systems.
Nguyen, T. H., & Ha, Q. P. (2016). Backstepping Control of Quadrotor UAVs with Adaptive Sliding Mode. IEEE Transactions on Aerospace and Electronic Systems.
Khalil, H. K. (2002). Nonlinear Systems. Prentice Hall.
Sun, C., & Wang, J. (2020). PID Control Design for UAV Path Tracking. Journal of Control Engineering and Applied Informatics.
(文章内容仅供参考,具体效果以图片为准)