LeetCode105.从前序与中序遍历构造二叉树

题目要求

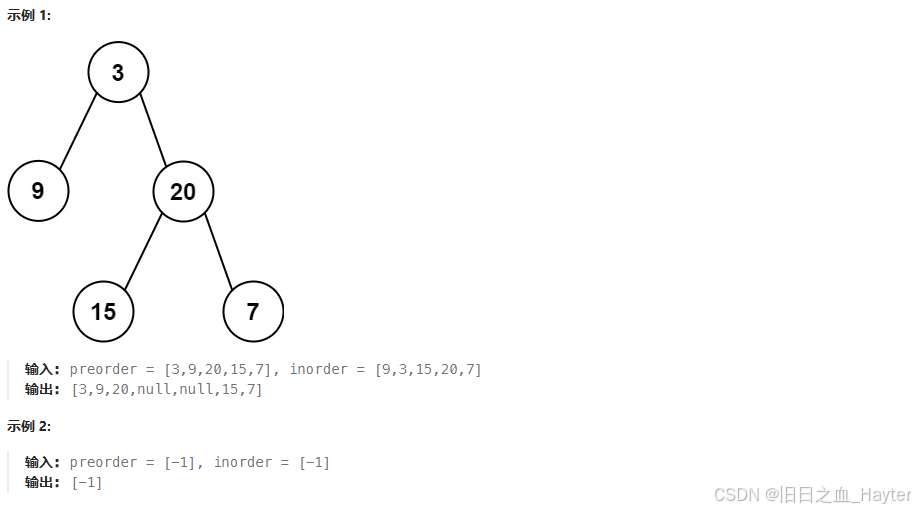
给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历 ， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

提示:

1 <= preorder.length <= 3000
inorder.length == preorder.length
-3000 <= preorder[i], inorder[i] <= 3000
preorder 和 inorder 均 无重复 元素
inorder 均出现在 preorder
preorder 保证为二叉树的前序遍历序列
inorder 保证为二叉树的中序遍历序列

解题思路

一般而言，知道一个二叉树的前序遍历和中序遍历就可以确定为唯一二叉树，前提是没有重复的子元素在里面。

在前序遍历中，我们知道一般是通过根左右的顺序进行遍历，所以我们可以在前序遍历中找到根节点，和当前根节点的左子树右子树的根节点。

而在中序遍历中，根节点的左边是所有左子树的节点，根节点的右边是所有右子树的节点，依此我们可以推断出左右子树的长度。

根据根节点，左右子树的长度作为条件，可以使用回溯的方式进行二叉树的构建。

算法流程

递推参数

根节点在前序遍历的索引 root 、子树在中序遍历的左边界 left 、子树在中序遍历的右边界 right 。

终止条件

当 left > right ，代表已经越过叶节点，此时返回 null 。

递推工作

建立根节点 node ：节点值为 preorder $root$ 。
划分左右子树：查找根节点在中序遍历 inorder 中的索引 i 。、
构建左右子树：开启左右子树递归。

代码解析

java 复制代码

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    Map<Integer, Integer> map;
    int[] preorder;
    int[] inorder;
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        //首先建立中序遍历的哈希表，方便根据根节点的值找到根节点的位置
        HashMap<Integer, Integer> map = new HashMap<>();
        for (int i = 0; i < inorder.length; i++) {
            map.put(inorder[i], i);
        }
        this.map = map;
        this.preorder = preorder;
        this.inorder = inorder;

        return recursion(0,0,inorder.length-1);
    }

    public TreeNode recursion(int root, int left, int right) {
        //终止条件
        if(left > right){
            return null;
        }
        //构建当前根节点
        TreeNode rootNode = new TreeNode(preorder[root]);
        //当前根节点在中序遍历中的索引位置
        int rootInOrderindex = map.get(preorder[root]);
        //开始递归构建左子树
        //左子树的根节点：当前根节点在前序遍历的索引+1，因为 根左右
        //左子树的左节点：在中序遍历中，第一个节点必定在左子树中，所以左子树的左节点必定是left = 0
        //左子树的右节点：中序遍历中，右节点必定是当前根节点在中序遍历中的索引位置-1
        rootNode.left = recursion(root+1,left,rootInOrderindex-1);
        //开始递归构建右子树
        //右子树的根节点：在前序遍历中，当前根节点加上左子树的长度之后，再加一个节点就是有字数的根节点
        //右子树的左节点：在中序遍历中，右子树的左节点一般是根节点在中序遍历中的索引+1
        //右子树的右节点：中序遍历中，右子树的右节点是中序遍历的最后一个节点
        rootNode.right = recursion(root + rootInOrderindex - left +1,rootInOrderindex+1,right);
        return rootNode;
    }
}