Floyd 算法精讲
题目描述
小明喜欢去公园散步,公园内布置了许多的景点,相互之间通过小路连接,小明希望在观看景点的同时,能够节省体力,走最短的路径。
给定一个公园景点图,图中有 N 个景点(编号为 1 到 N),以及 M 条双向道路连接着这些景点。每条道路上行走的距离都是已知的。
小明有 Q 个观景计划,每个计划都有一个起点 start 和一个终点 end,表示他想从景点 start 前往景点 end。由于小明希望节省体力,他想知道每个观景计划中从起点到终点的最短路径长度。 请你帮助小明计算出每个观景计划的最短路径长度。
输入描述
第一行包含两个整数 N, M, 分别表示景点的数量和道路的数量。
接下来的 M 行,每行包含三个整数 u, v, w,表示景点 u 和景点 v 之间有一条长度为 w 的双向道路。
接下里的一行包含一个整数 Q,表示观景计划的数量。
接下来的 Q 行,每行包含两个整数 start, end,表示一个观景计划的起点和终点。
输出描述
对于每个观景计划,输出一行表示从起点到终点的最短路径长度。如果两个景点之间不存在路径,则输出 -1。
输入示例
7 3 2 3 4 3 6 6 4 7 8 2 2 3 3 4输出示例
4 -1提示信息
从 2 到 3 的路径长度为 4,3 到 4 之间并没有道路。
1 <= N, M, Q <= 1000.
1 <= w <= 10000.
思路
多源最短路,即 求多个起点到多个终点的多条最短路径。
Floyd 算法对边的权值正负没有要求,都可以处理。
Floyd算法核心思想是动态规划。那么就应用五部曲思路来解
1.grid[i][j][k] = m,表示 节点i 到 节点j 以[1...k] 集合为中间节点的最短距离为m。
分两种情况:
- 节点i 到 节点j 的最短路径经过节点k
- 节点i 到 节点j 的最短路径不经过节点k
对于第一种情况,grid[i][j][k] = grid[i][k][k - 1] + grid[k][j][k - 1]
节点i 到 节点k 的最短距离 是不经过节点k,中间节点集合为[1...k-1],所以 表示为grid[i][k][k - 1]
节点k 到 节点j 的最短距离 也是不经过节点k,中间节点集合为[1...k-1],所以表示为 grid[k][j][k - 1]
第二种情况,grid[i][j][k] = grid[i][j][k - 1]
如果节点i 到 节点j的最短距离 不经过节点k,那么 中间节点集合[1...k-1],表示为 grid[i][j][k - 1]
因为我们是求最短路,对于这两种情况自然是取最小值。
即: grid[i][j][k] = min(grid[i][k][k - 1] + grid[k][j][k - 1], grid[i][j][k - 1])
k 赋值为 0,本题 节点0 是无意义的,节点是从1 到 n。
这样我们在下一轮计算的时候,就可以根据 grid[i][j][0] 来计算 grid[i][j][1],此时的 grid[i][j][1] 就是 节点i 经过节点1 到达 节点j 的最小距离了。grid是一个三维数组。
i 和j 是平层,而k 是 垂直向上 的。
遍历的顺序是从底向上 一层一层去遍历。
所以遍历k 的for循环一定是在最外面,这样才能一层一层去遍历。如图:
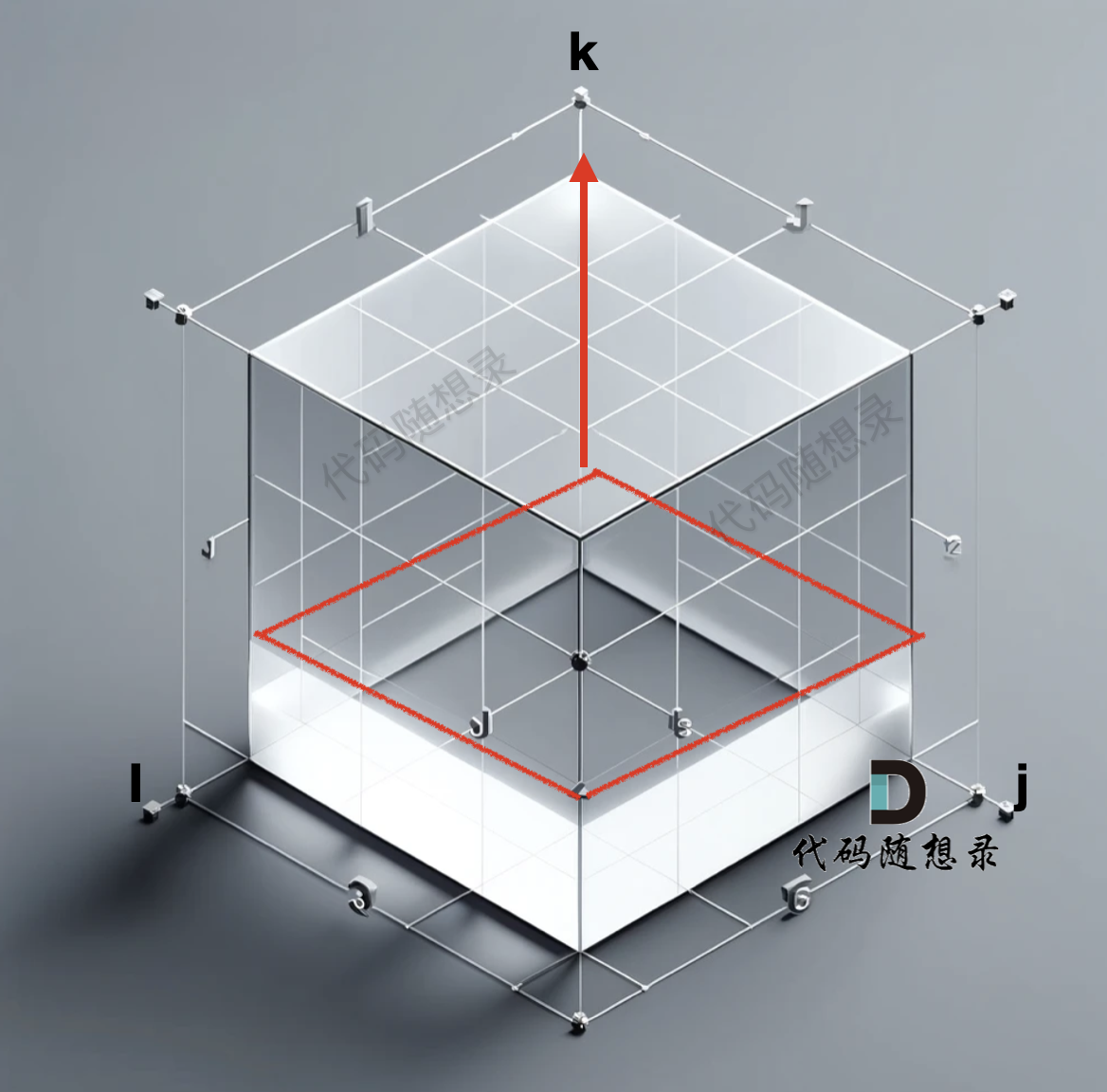
至于遍历 i 和 j 的话,for 循环的先后顺序无所谓。
5.举例打印dp数组
代码
#include <iostream>
#include <vector>
#include <list>
using namespace std;
int main()
{
int n,m,p1,p2,val;
cin>>n>>m;
//声明一个三维向量 grid,用于存储所有节点对之间的最短路径。grid[i][j][k] 表示在考虑前 k 个节点作为中间节点时,从节点 i 到节点 j 的最短路径。
vector<vector<vector<int>>>grid(n+1,vector<vector<int>>(n+1,vector<int>(n+1,10005)));
for(int i=0;i<m;i++)
{
cin>>p1>>p2>>val;
grid[p1][p2][0]=val;//将边 p1 到 p2 的权重存储在 grid[p1][p2][0] 中。
grid[p2][p1][0]=val;//因为这是双向图,所以同时将边 p2 到 p1 的权重存储在 grid[p2][p1][0] 中。
}
//Floyd-Warshall 算法核心
for(int k=1;k<=n;k++)//遍历所有可能的中间节点 k。
{
for(int i=1;i<=n;i++)
{
for(int j=1;j<=n;j++)
{
//更新从节点 i 到节点 j 的最短路径。
//grid[i][j][k-1] 表示不经过节点 k 时的最短路径,
//grid[i][k][k-1] + grid[k][j][k-1] 表示经过节点 k 时的最短路径。
//取两者中的最小值。
grid[i][j][k]=min(grid[i][j][k-1],grid[i][k][k-1]+grid[k][j][k-1]);
}
}
}
int z,start,end;//观景计划z、起始节点 start 和目标节点 end。
cin>>z;
while(z--)
{
cin>>start>>end;
if(grid[start][end][n]==10005)cout<<-1<<endl;
else cout<<grid[start][end][n]<<endl;
}
}模拟运行结果
4 5 1 2 1 1 3 4 2 3 1 3 4 1 4 1 5 3 1 4 2 4 1 3
首先读取
n=4和m=5,初始化邻接矩阵grid。读取边并初始化邻接矩阵:
- 边
(1, 2, 1),grid[1][2][0] = 1,grid[2][1][0] = 1- 边
(1, 3, 4),grid[1][3][0] = 4,grid[3][1][0] = 4- 边
(2, 3, 1),grid[2][3][0] = 1,grid[3][2][0] = 1- 边
(3, 4, 1),grid[3][4][0] = 1,grid[4][3][0] = 1- 边
(4, 1, 5),grid[4][1][0] = 5,grid[1][4][0] = 5运行 Floyd-Warshall 算法:
- 第一轮(
k=1):
- 更新
grid[1][2][1],grid[1][3][1],grid[1][4][1],grid[2][1][1],grid[3][1][1],grid[4][1][1]- 第二轮(
k=2):
- 更新
grid[1][2][2],grid[1][3][2],grid[1][4][2],grid[2][1][2],grid[2][3][2],grid[2][4][2],grid[3][2][2],grid[4][2][2]- 第三轮(
k=3):
- 更新
grid[1][3][3],grid[1][4][3],grid[2][3][3],grid[2][4][3],grid[3][1][3],grid[3][2][3],grid[3][4][3],grid[4][3][3]- 第四轮(
k=4):
- 更新
grid[1][4][4],grid[2][4][4],grid[3][4][4],grid[4][1][4],grid[4][2][4],grid[4][3][4]读取查询次数
z=3并处理每个查询:
- 查询
(1, 4):grid[1][4][4] = 3,输出3- 查询
(2, 4):grid[2][4][4] = 2,输出2- 查询
(1, 3):grid[1][3][4] = 2,输出2最终输出:
3 2 2
A * 算法精讲 (A star算法)
题目描述
在象棋中,马和象的移动规则分别是"马走日"和"象走田"。现给定骑士的起始坐标和目标坐标,要求根据骑士的移动规则,计算从起点到达目标点所需的最短步数。
棋盘大小 1000 x 1000(棋盘的 x 和 y 坐标均在 [1, 1000] 区间内,包含边界)
输入描述
第一行包含一个整数 n,表示测试用例的数量,1 <= n <= 100。
接下来的 n 行,每行包含四个整数 a1, a2, b1, b2,分别表示骑士的起始位置 (a1, a2) 和目标位置 (b1, b2)。
输出描述
输出共 n 行,每行输出一个整数,表示骑士从起点到目标点的最短路径长度。
输入示例
6 5 2 5 4 1 1 2 2 1 1 8 8 1 1 8 7 2 1 3 3 4 6 4 6输出示例
2 4 6 5 1 0提示信息
骑士移动规则如图,红色是起始位置,黄色是骑士可以走的地方。
思路
Astar 是一种 广搜的改良版。
我们在搜索最短路的时候, 如果是无权图(边的权值都是1) 那就用广搜,代码简洁,时间效率和 dijkstra 差不多 (具体要取决于图的稠密)
如果是有权图(边有不同的权值),优先考虑 dijkstra。
BFS 是没有目的性的 一圈一圈去搜索, 而 A * 是有方向性的去搜索。
从队列里取出什么元素,接下来就是从哪里开始搜索。
所以 启发式函数 要影响的就是队列里元素的排序!
对队列里节点进行排序,就需要给每一个节点权值,如何计算权值呢?
每个节点的权值为F,给出公式为:F = G + H
G:起点达到目前遍历节点的距离
H:目前遍历的节点到达终点的距离
起点达到目前遍历节点的距离 + 目前遍历的节点到达终点的距离 就是起点到达终点的距离。
本题的图是无权网格状,在计算两点距离 通常有如下三种计算方式:
- 曼哈顿距离,计算方式: d = abs(x1-x2)+abs(y1-y2)
- 欧氏距离(欧拉距离) ,计算方式:d = sqrt( (x1-x2)^2 + (y1-y2)^2 )
- 切比雪夫距离,计算方式:d = max(abs(x1 - x2), abs(y1 - y2))
x1, x2 为起点坐标,y1, y2 为终点坐标 ,abs 为求绝对值,sqrt 为求开根号,
本题采用欧拉距离 才能最大程度体现 点与点之间的距离。
代码
/A* 算法是一种启发式搜索算法,
//结合了 Dijkstra 算法和贪心算法的特点,
//通过评估函数 F = G + H 来选择最优路径。
#include <iostream>
#include <queue>
#include <string.h>//引入字符串处理库,这里主要用于 memset 函数。
using namespace std;
int moves[1001][1001];
//骑士的8个可能移动方向。
int dir[8][2]={-2,-1,-2,1,-1,2,1,2,2,1,2,-1,1,-2,-1,-2};
int b1,b2;//目标位置的坐标
struct Knight//表示骑士的状态。
{
int x,y;//骑士的当前位置。
int g,h,f;
//从起点到当前节点的路径消耗,表示从当前节点到目标节点的预估消耗。表示总评估值 F = G + H。
//重载小于运算符,使优先队列按 f 值从小到大排序。
bool operator<(const Knight &k)const{
return k.f<f;
}
};
priority_queue<Knight> que;
//定义启发式函数
int Heuristic(const Knight&k)//欧拉距离
{
return (k.x-b1)*(k.x-b1)+(k.y-b2)*(k.y-b2);
}
//实现A* 算法
void astar(const Knight& k)
{
Knight cur,next;
que.push(k);//将起始节点 k 推入优先队列。
while(!que.empty())
{
cur=que.top();que.pop();//取出优先队列中的最小 f 值节点。
if(cur.x==b1&&cur.y==b2)break;//如果当前节点是目标节点,结束搜索。
for(int i=0;i<8;i++)//遍历骑士的8个可能移动方向。
{
next.x=cur.x+dir[i][0];
next.y=cur.y+dir[i][1];
//检查下一个节点是否在棋盘范围内。
if(next.x<1||next.x>1000||next.y<1||next.y>1000)continue;
if(!moves[next.x][next.y])//如果下一个节点未被访问过,进行以下操作
{
moves[next.x][next.y]=moves[cur.x][cur.y]+1;//更新下一个节点的步数。
next.g=cur.g+5;//更新下一个节点的 g 值,马走日的步长为 sqrt(1^2 + 2^2) = sqrt(5)
next.h=Heuristic(next);//计算下一个节点的 h 值。
next.f=next.g+next.h;
que.push(next);
}
}
}
}
int main()
{
int n,a1,a2;//测试用例数 n 和起始位置的坐标 a1 和 a2。
cin>>n;
while(n--)
{
cin>>a1>>a2>> b1>>b2;
//初始化 moves 数组,将其所有元素设为 0。
memset(moves,0,sizeof(moves));
Knight start;
start.x=a1;//设置起始节点的坐标。
start.y=a2;
start.g=0;
start.h=Heuristic(start);
start.f=start.g+start.h;
astar(start);//设置起始节点的坐标。
while(!que.empty())que.pop();//队列清空
cout<<moves[b1][b2]<<endl;//输出从起始位置到目标位置的最短步数。
}
return 0;
}模拟运行结果
2 1 1 8 8 1 1 2 2
- 首先读取测试用例数
n=2。第一个测试用例
- 起始位置
(1, 1),目标位置(8, 8)。- 初始化
moves数组。- 创建起始节点
start,计算g、h和f值。- 调用
astar(start),执行 A* 算法。- 输出从
(1, 1)到(8, 8)的最短步数。第二个测试用例
- 起始位置
(1, 1),目标位置(2, 2)。- 初始化
moves数组。- 创建起始节点
start,计算g、h和f值。- 调用
astar(start),执行 A* 算法。- 输出从
(1, 1)到(2, 2)的最短步数。最终输出
6 2
最短路算法总结篇
四大最短路算法,分别是Dijkstra、Bellman_ford、SPFA 和 Floyd。

大体使用场景的分析
如果遇到单源且边为正数,直接Dijkstra 。使用朴素版还是 堆优化版 还是取决于图的稠密度.
如果遇到单源边可为负数,直接 Bellman-Ford,同样 SPFA 还是 Bellman-Ford 取决于图的稠密度。一般情况下,直接用 SPFA。
如果有负权回路,优先 Bellman-Ford, 如果是有限节点最短路 也优先 Bellman-Ford,理由是写代码比较方便。
如果是遇到多源点求最短路,直接 Floyd。除非 源点特别少,且边都是正数,那可以 多次 Dijkstra 求出最短路径,但这种情况很少,一般出现多个源点了,就是想让你用 Floyd 了。
对于A * ,由于其高效性,所以在实际工程应用中使用最为广泛 ,由于其 结果的不唯一性,也就是可能是次短路的特性,一般不适合作为算法题。
游戏开发、地图导航、数据包路由等都广泛使用 A * 算法。
图论总结
从深搜广搜 到并查集,从最小生成树到拓扑排序, 最后是最短路算法系列。
深搜与广搜是图论里基本的搜索方法,大家需要掌握三点:
- 搜索方式:深搜是可一个方向搜,不到黄河不回头。 广搜是围绕这起点一圈一圈的去搜。
- 代码模板:需要熟练掌握深搜和广搜的基本写法。
- 应用场景:图论题目基本上可以即用深搜也可用广搜,无疑是用哪个方便而已
并查集
- 为什么要用并查集,怎么不用个二维数据,或者set、map之类的。
- 并查集能解决那些问题,哪些场景会用到并查集
- 并查集原理以及代码实现
- 并查集写法的常见误区
- 带大家去模拟一遍并查集的过程
- 路径压缩的过程
- 时间复杂度分析
最小生成树
最小生成树是所有节点的最小连通子图, 即:以最小的成本(边的权值)将图中所有节点链接到一起。
最小生成树算法,有prim 和 kruskal。
prim 算法是维护节点的集合,而 Kruskal 是维护边的集合。
在 稀疏图中,用Kruskal更优。 在稠密图中,用prim算法更优。
prim算法三部曲
- 第一步,选距离生成树最近节点
- 第二步,最近节点加入生成树
- 第三步,更新非生成树节点到生成树的距离(即更新minDist数组)
kruscal的主要思路:
- 边的权值排序,因为要优先选最小的边加入到生成树里
- 遍历排序后的边
- 如果边首尾的两个节点在同一个集合,说明如果连上这条边图中会出现环
- 如果边首尾的两个节点不在同一个集合,加入到最小生成树,并把两个节点加入同一个集合
给出一个 有向图,把这个有向图转成线性的排序 就叫拓扑排序。
- 找到入度为0 的节点,加入结果集
- 将该节点从图中移除
最后是最短路算法,好多好多题目,一刷只能理解并跟着写代码。
