Transformer-Squared:停止微调 LLMs
自适应大语言模型背后的架构、Transformer-Squared 的数学与代码,以及奇异值分解

DALL-E 生成的图片我们已经进入了这样一个时代:AI 能够写出惊人连贯的文章,回答复杂问题,甚至生成代码。这确实令人叹为观止。但如果你曾真正用这些模型来处理具体任务,你可能会遇到和我一样的问题:那就是不可避免的微调需求。想让你的 LLM 精通编程?微调它。需要它解决数学难题?再微调。微调已经成为默认方法,甚至可以说是业内的一种本能反应。
说实话,微调确实有效。它让我们得以把这些通用的大型模型塑造成更加专业、更加实用的工具。然而,换个角度想一想,我们不得不问:这种不断微调的循环,真的是最有效、最优雅的解决方案吗? 微调的计算成本极高,耗时耗力,而且每次微调,我们本质上都在创建一个新的、相对静态的模型版本。那当我们需要它转向另一个任务,或者进入一个全新的领域时怎么办?没错------还得再微调。这样一来,就好像每次想在不同类型的道路上行驶,我们都得重新组装一台发动机。
有没有更聪明的方法?如果我们的 LLM 不用经历这些高强度、全面的再训练过程,而是能在实际任务处理中自适应调整,像是在实时思考并动态调整内部机制,那会怎样?
这正是 Sun、Cetin 和 Tang 在 Sakana AI 提出的最新论文 "Transformer-Squared: Self-adaptive LLMs"(Transformer²:自适应大语言模型)中的核心设想。他们引入了一种名为 Transformer² 的框架,大胆地提出,我们或许可以摆脱对微调的持续依赖。
这个核心思路围绕着奇异值分解(Singular Value Decomposition, SVD)展开。听起来很复杂?别担心,我们稍后会详细拆解。简单来说,Transformer² 让 LLM 可以在回答问题的过程中,动态调整自身的内部机制------就像拧几个关键的旋钮和调节器,而不是事先进行大规模的参数调整。
他们通过一种称为奇异值微调(Singular Value Fine-tuning, SVF)的技术来实现这一目标,并结合了强化学习(Reinforcement Learning)。这个方法采用双通推理机制:模型首先分析输入任务,确定需求,然后在生成最终输出之前调整自身。
这个方法令人瞩目的原因有几个:
-
更高的效率 ------ 想象一下,如果我们不需要为每个特定应用进行微调,而是能动态适应,能节省多少计算资源?
-
更强的灵活性 ------ 模型不再那么僵硬,而是可以即刻调整,不局限于单一用途。
-
更接近人类的学习方式 ------ 我们人类的学习方式不是完全推翻旧知识,而是根据情境动态调整思维。
当然,这种方法是否真的适用于各种任务?它的泛化能力如何?有什么限制?这些正是本文将要探讨的问题。我们会深入研究 Transformer² 的数学原理,拆解代码概念,并讨论这一创新框架可能会对 AI 未来产生怎样的影响。那么,你准备好探索 LLM 自适应未来 了吗?让我们深入研究。
Transformer-Squared

动画来自 Transformer-Squared 原始代码库Transformer²,由Sun及其同事提出,带来了一种范式转变。与其将大语言模型(LLM)的调整视为一种全面的重新训练,他们设想了一种模型,它可以在遇到新任务时灵活地调整自己。这有点像从单速自行车换成变速自行车------突然之间,你可以适应上坡、逆风和不同的地形,而无需从根本上改变整辆自行车,只需智能地换挡。Transformer² 旨在为 LLM 配备类似的动态换挡机制。
如果你愿意称其为"魔法",那么它的起点是一个相当优雅的数学概念:奇异值分解(Singular Value Decomposition, SVD)。把 SVD 想象成一种解析矩阵的方法------在神经网络的世界里,到处都是权重矩阵,而 SVD 就是把这些矩阵拆解成它们的基本组成部分。想象一下,你有一个复杂的食谱。SVD 就像是把它分解成一系列更简单、彼此正交的烹饪技巧,每种技巧都为最终的菜肴贡献独特的风味或质感。从数学上讲,SVD 告诉我们,任何矩阵------我们称之为 W------都可以分解成三个其他矩阵:U、Σ 和 V^T。至关重要的是,Σ 是一个对角矩阵,其中包含我们称之为"奇异值"的内容。从某种意义上说,这些奇异值代表了这些基本组成部分的"重要性"或"强度"。这就像是在识别真正定义你复杂食谱的核心食材和技术。
Transformer² 通过一种称为奇异值微调(Singular Value Fine-tuning, SVF)的方法来利用 SVD 这一洞见。SVF 的核心思想很简单,但乍一看可能有点违反直觉。与其在微调过程中调整权重矩阵的所有无数参数(这是传统方法,甚至一些参数高效方法通常采用的做法),SVF 只专注于调整这些奇异值,也就是 UΣV^T 分解中的 Σ 部分。他们使用了一种称为"专家向量"(expert vectors)的手段来实现这一点。想象一下,你有一组专精于不同菜系的厨师。这些"专家向量"就像是这些厨师的烹饪档案,编码了他们特定的技能和风格。在训练过程中,Transformer² 通过强化学习(Reinforcement Learning)学习这些"专家向量",每个向量都针对特定类型的任务,例如编码、数学或推理。这里的高明之处在于其高效性:通过仅学习这些相对较小的"专家向量"来调整奇异值,SVF 相比修改模型权重大块参数的方法,变得极其高效。这就像是给每位厨师提供一小套调味料,微妙地调整他们的基础食谱,而不是为了每道新菜肴重新编写整本烹饪手册。
但这如何转化为实时适应能力呢?这就是 Transformer² 的两遍推理机制(two-pass inference mechanism)发挥作用的地方。把它想象成一个两步过程:"理解任务,然后调整并回答。"在第一遍时,当你给 Transformer² 一个提示------一个问题、一个请求,或任何输入------模型会先使用其基础的预训练权重进行初步处理。这一遍并不用于生成最终答案,而更像是在"评估形势",尝试理解当前任务的性质。基于这个初步评估,Transformer² 进入第二遍。在这里,模型会动态选择并混合之前提到的预训练"专家向量"。如果第一遍的分析表明任务与数学密切相关,它可能会强调"数学专家向量"。如果任务似乎需要逻辑推理,它可能会倾向于"推理专家向量"。这种专家向量的混合过程实际上是在实时调整模型的权重矩阵,使其适应输入提示的具体需求。然后,使用这些调整后的权重,模型执行第二遍推理,并生成最终答案。
Transformer² 方法的潜在优势颇具吸引力。首先,也是最实际的一点,它承诺更高的效率。通过绕过全面微调,仅专注于这些轻量级的专家向量,它可以显著降低 LLM 适应新任务的计算开销。其次,它暗示了一种新的实时适应能力。想象一下,一个 LLM 可以流畅地在不同的技能集之间切换,而无需为每个技能集单独进行显式的重新训练。这可能会带来更加多才多艺、更加灵活的 AI 系统。第三,这种方法的通用性也令人向往。论文表明,Transformer² 并不局限于特定的 LLM 架构;它可能适用于不同的模型,甚至跨模态,如视觉-语言任务。
当然,现在还处于早期阶段。我们需要对 Transformer² 在实践中的表现进行严格评估,涵盖广泛的任务和真实世界场景。这些"专家向量"真的捕捉到了有意义的技能吗?这种动态适应机制有多强大?是否存在我们尚未发现的局限性?这些都是关键问题,而要开始解答它们,我们需要更深入地研究 Transformer² 的数学核心。让我们来拆解那些公式,看看其底层到底发生了什么。
Transformer-Squared 背后的数学
好了,让我们戴上数学帽,深入探究 Transformer² 的内部机制。别担心,我们会尽量保持接地气,专注于核心思想,而不会迷失在过于复杂的方程式里。目标是理解支撑这种动态适应的数学运算,并欣赏这种方法的优雅之处,以及它可能存在的局限性。
正如我们之前讨论的,基础是奇异值分解(Singular Value Decomposition,SVD)。如果我们有一个权重矩阵 W,可以把它想象成一种转换,它在数据流经神经网络的过程中重新塑造和调整数据。SVD 允许我们将这种复杂的转换分解成一系列更简单、更基础的转换。从数学上讲,我们可以表示为:
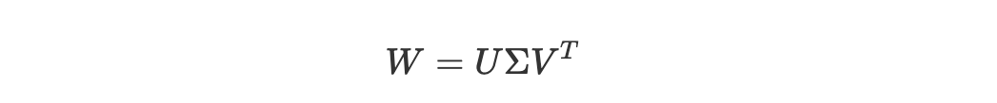
奇异值分解 --- 作者自制图让我们分解每个组成部分:
• U 和 V 是所谓的半正交矩阵。可以把它们想象成一组正交坐标轴------即在空间中彼此垂直的方向。U 代表输出方向,而 V 代表输入方向。
• Σ 是我们讨论的核心部分。它是一个对角矩阵,也就是说,它的对角线上有值,而其他地方都是零。这些对角线上的值 σ_i 称为奇异值。它们始终是非负的,并且通常按照从大到小排序。每个 σ_i 本质上决定了 V 的列和 U 的列相应部分在整体变换中的贡献大小。
那么,这在实际中意味着什么?当我们执行矩阵乘法 y=Wxy = Wxy=Wx 时,我们可以用 SVD 分解重写它,如下所示:
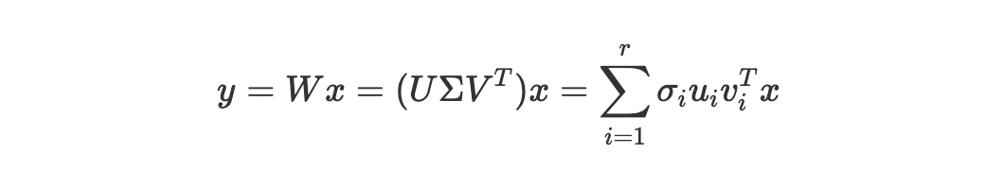
SVD 矩阵乘法 --- 作者自制图在这里,uiu_iui 和 viv_ivi 分别是 U 和 V 的第 i 列,而 r 是矩阵 W 的秩(rank)。这个方程传达了一个非常深刻的思想:复杂的变换 W 实际上是多个简单的秩一(rank-one)变换的总和,每个变换由一个奇异值 σi\sigma_iσi 进行缩放。换句话说,就像一个复杂的旋律是由多个简单的音符组合而成,而奇异值决定了每个音符的音量或重要性。
现在进入关键部分:奇异值微调(Singular Value Fine-tuning,SVF)。
Transformer² 的创新之处在于,它意识到我们不需要调整整个权重矩阵 W 来改变它的行为。相反,我们可以只调整奇异值 Σ 来实现针对性的修改。他们提出学习一个向量,称之为"专家向量"(expert vector),我们可以用 z 来表示。这个向量 z 的维度与奇异值的数量相同。SVF 通过逐元素乘法来修改原始奇异值矩阵 Σ,从而得到一个新的矩阵 Σ′:
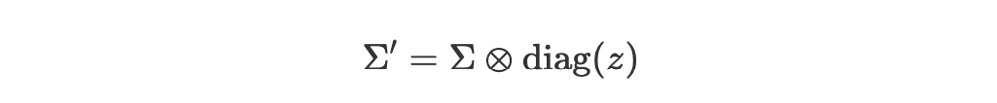
奇异值微调 --- 作者自制图在这里,diag(z) 从向量 z 创建一个对角矩阵,而 ⊗ 表示逐元素乘法。基本上,专家向量的每个元素 ziz_izi 负责缩放相应的奇异值 σi\sigma_iσi。新的适配后权重矩阵 W′ 变成:
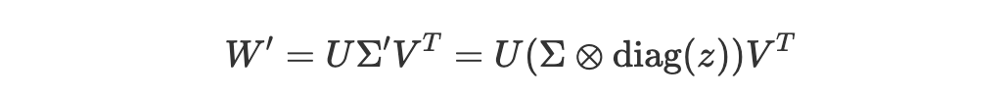
SVD 与 SVF --- 作者自制图请注意,U 和 V 仍然保持 W 原始 SVD 分解时的值不变。只有对角矩阵 Σ 受专家向量 z 的影响进行了修改。这正是 SVF 在参数上高效的核心:我们仅仅学习了一个相对较小的向量 z,而不是直接修改庞大的 U、Σ 和 V 矩阵。
在 两遍推理(two-pass inference) 过程中,第一遍使用的是原始权重矩阵 W。假设输入提示是 x,第一遍的隐藏状态可以概念化地表示为:h1=LLM(x;W).
这些隐藏状态随后用于确定合适的"专家向量",我们称之为 z′。适配发生在第二遍。在第二遍中,权重矩阵使用所选的专家向量 z′ 进行修改,变为 W'_adapted′ = U(Σ ⊗ diag(z′))V^T。最后,使用这些适配后的权重生成输出 y:y = LLM(x ; W'_adapted)。
z′ 的选择取决于"适配策略"(adaptation strategy)------无论是基于提示的分类器、专门的分类器,还是更复杂的少样本(few-shot)适配方法,我们稍后会详细讨论。
为了训练这些专家向量 z,作者使用了强化学习(Reinforcement Learning,RL)。这与预训练和标准微调中通常使用的下一标记预测目标不同,而是直接针对任务性能进行优化。对于一个给定的提示 x_i 和生成的答案 y^i,定义了一个奖励 r(y^i, y_i),基于生成的答案与真实答案 y_i 之间的正确性来计算。他们希望最大化的目标函数 J(θ_z)(简化形式)如下所示:
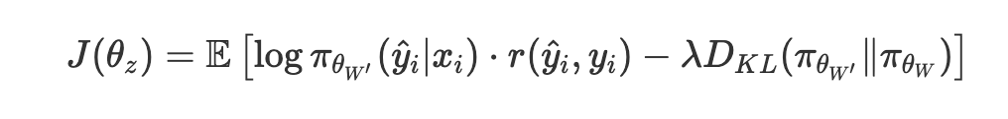
目标函数 --- 作者自制图虽然这个公式看起来有点复杂,但关键部分是:
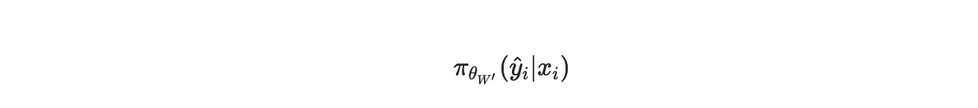
目标函数的概率成分 --- 作者自制图这表示在适配后的模型权重 W′W'W′ 下,生成答案 yiy^iyi 的概率。

目标函数的奖励成分 --- 作者自制图这是奖励信号,衡量生成的答案质量。
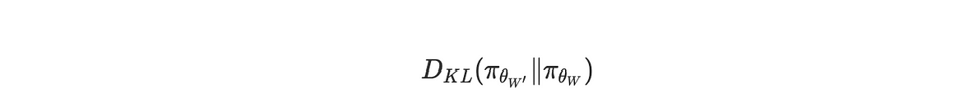
目标函数的散度成分 --- 作者自制图这是一个 KL 散度项,用于惩罚适配后的模型π_θ_W′ 过度偏离原始模型 π_θ_W。这起到了正则化作用,防止模型发生剧烈变化,并保留基础模型的一些通用能力。
最后,λ是一个系数,用于控制这个正则化的强度。
从本质上讲,RL 目标鼓励专家向量调整模型,使其在特定任务上最大化奖励,同时由于 KL 散度惩罚,保持这些变化在一定范围内,不会偏离原始模型太远。
与传统微调相比,SVF 只修改奇异值,而不是直接调整整个模型的参数。即使是像 LoRA 这样的参数高效方法,它们仍然需要引入额外的低秩矩阵,而 SVF 通过直接操作奇异值,实现了一种根本不同且可能更高效的方式。它直接作用于权重矩阵的核心"强度",允许在最小参数开销下进行细致入微的任务适配。
不过,也需要考虑可能的局限性。仅仅修改奇异值,是否足以捕捉所有任务所需的完整适配?在某些场景下,这种方法会不会过于受限?这些都是需要思考的问题。随着我们继续探索 Transformer² 及其实际应用,这些问题值得进一步研究。但至少目前,希望这个数学解析能让你对这个自适应 LLM 框架的精妙机制有更清晰的认识。
Transformer-Squared 背后的代码
研究人员在论文发布的同时提供了一个 GitHub 仓库,我们将在本文的这一部分对其进行剖析,以理解如何将上述数学公式转换为可执行的代码。
整体概述
让我们快速总结一下到目前为止所说的一切,然后准备进入有趣的部分。传统的微调方法会更新模型的许多参数。而 Transformer² 提出了一种不同的方法:仅"微调"权重矩阵的"强度",通过 SVD 进行分解,然后只调整奇异值。在实践中,这意味着对于给定的权重矩阵

SVD 公式 --- 作者自制图该框架学习一个小的"专家向量" z,它通过逐元素操作来调节奇异值(Σ 的对角元素)。新的权重矩阵变成类似于
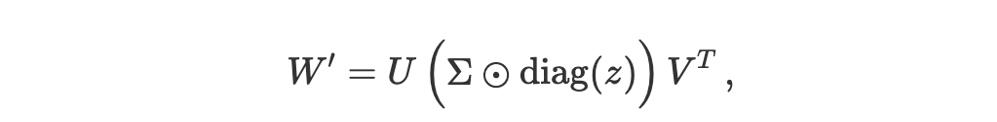
带有 SVD 的 SVF 公式 --- 作者自制图可能还会有一个缩放因子来保持整体幅度。这就是"奇异值微调"(Singular Value Fine-tuning,SVF)的核心:与其重新优化数百万个参数,不如仅使用强化学习(RL)来学习一个紧凑的向量。
提供的脚本实现了这个想法。它们(1)通过 SVD 分解某些层的权重,(2)定义一个"策略"(或一组专家向量),用于生成掩码或系数来修改奇异值,(3)在需要时组合(甚至混合)多个专家向量,并且(4)使用一个两遍评估机制,先对提示进行分类,然后应用相应的"专家"调整。现在让我们来逐步解析这些文件。
主程序: svd_reinforce_hydra.py
这个脚本负责协调整个适配过程,训练学习专家向量的"策略",然后将其应用到模型中。
它使用 Hydra 和 OmegaConf 来加载实验设置(迭代次数、批量大小、随机种子、是否仅运行测试模式等)。
@hydra.main(version_base=None, config_path="cfgs", config_name="config")
def main(cfg):
...
这种结构允许进行动态配置管理,所有参数------从训练迭代次数到模型选择------都可以在 YAML 文件中指定。该脚本的配置处理尤为精细,如在 wandb 初始化中所示:
def wandb_init(cfg, run_name: str, group_name: str, log_dir: str):
config_dict = OmegaConf.to_container(
cfg,
resolve=True,
throw_on_missing=False,
)
config_dict["log_dir"] = log_dir
config_dict["wandb_run_name"] = run_name
config_dict["wandb_group_name"] = group_name
这段代码将 Hydra 的 OmegaConf 配置转换为适合实验追踪的格式,确保所有参数被正确记录,并使实验具有可复现性。
模型初始化阶段尤其有趣。看看脚本是如何处理 SVD 分解的:
if not os.path.exists(decomposed_param_file):
print("Decomposed params not found. Decomposing...")
decomposed_params = {}
for k, v in base_params.items():
if "norm" not in k:
print(k)
U, S, V = torch.svd(v)
decomposed_params[f"{k}.U"] = U
decomposed_params[f"{k}.S"] = S
decomposed_params[f"{k}.V"] = V
torch.save(decomposed_params, decomposed_param_file)
这对模型的权重矩阵执行 SVD,但关键是它是有选择性的------注意 if "norm" not in k 这个条件。这意味着它只对特定的层进行分解,避免在归一化层上执行不必要的计算,因为 SVD 在这些层上并无实际意义。
这与 SVD 相对应:
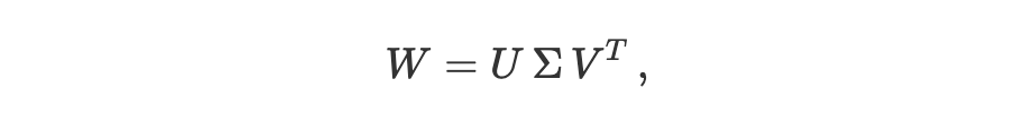
其中 Σ(这里称为 S)包含了奇异值,这些值用于"衡量每个方向的重要性"。
策略初始化和优化设置展示了系统的灵活性:
policy: Policy = hydra.utils.instantiate(
cfg.shakeoff_policy,
base_params=base_params,
decomposed_params=decomposed_params,
gpu=gpu,
)
optimization_algorithm: OptimizationAlgorithm = hydra.utils.instantiate(
cfg.optimization_algorithm,
policy=policy,
gpu=gpu,
)
它通过 Hydra 的配置系统实例化了策略网络及其优化算法。策略负责生成"专家向量",用于调节奇异值,而优化算法则根据任务性能决定如何更新这些向量。
检查点加载系统尤其健壮:
if resuming_from_ckpt and os.path.exists(load_ckpt):
if use_lora:
assert os.path.isdir(load_ckpt), "ckpt for lora must be dir to lora adapter"
from peft import PeftModel
lora_model = PeftModel.from_pretrained(model, load_ckpt)
merged_model = lora_model.merge_and_unload()
new_params = merged_model.state_dict()
elif "learnable_params" in load_ckpt:
learnable_params = torch.load(load_ckpt)
for k, v in learnable_params.items():
learnable_params[k] = v.to(gpu)
它处理多种类型的检查点------标准模型状态、LoRA 适配,以及学习得到的参数向量。系统可以无缝地从这些格式中的任何一种恢复训练。
训练循环实现了一个复杂的优化过程:
for i in range(num_iters):
batch_ix = np_random.choice(train_ix, size=clipped_batch_size, replace=False)
optimization_algorithm.step_optimization(
model_id=model_id,
model=model,
tokenizer=tokenizer,
policy=policy,
task_loader=task_loader,
batch_ix=batch_ix,
train_data=train_data,
train_eval=train_eval,
base_params=base_params,
decomposed_params=decomposed_params,
original_model_params=original_model_params,
metrics_to_log=metrics_to_log,
vllm_model=vllm_model,
)
每次迭代都会随机抽取一批训练数据,并通过优化算法进行处理。step_optimization 方法负责处理以下复杂过程:
-
应用当前策略来修改奇异值
-
在该批数据上运行修改后的模型
-
计算奖励信号
-
更新策略参数
评估系统尤其复杂:
if test_only and prompt_based_eval:
test_data_dict = eval_model_experts_prompt_based(
vllm_model,
test_eval,
experts_path_dict,
policy,
model,
base_params,
decomposed_params,
task_loader.target_metric_test,
)
这实现了两阶段评估系统,首先对输入进行分类,然后使用合适的专家向量进行处理。评估结果被全面记录:
data_dict = {
"iter": i,
"best_val_acc": best_val_acc,
"test_at_best_val": test_at_best,
"train_acc": train_res.aggregate_metrics[task_loader.target_metric_train],
"valid_acc": valid_res.aggregate_metrics[task_loader.target_metric_valid],
"test_acc": test_res.aggregate_metrics[task_loader.target_metric_test],
**metrics_to_log.get(),
}
日志系统不仅记录基本指标,还详细捕捉了关于策略行为和参数分布的统计数据。这种全面的日志记录对于理解适配过程和调试问题至关重要。
策略与优化
Policy 类(policy/base.py)继承自 PyTorch 的 nn 模块,并实现了生成和管理"专家向量"的核心逻辑,这些向量用于调节模型的奇异值。首先,让我们来看初始化部分:
def init(self, base_params, gpu, init_val, max_mult=1, **kwargs):
super().init()
self.learnable_params = {}
self.num_params = 0
self.max_mult = max_mult
这个设置建立了关键参数,包括 max_mult,它限制了奇异值的最大乘法因子,以防止极端修改导致模型不稳定。
核心参数的初始化发生在以下循环中:
for k, v in base_params.items():
if "mlp" in k:
self.learnable_params[k] = torch.nn.Parameter(
data=(
torch.randn(
min(v.shape),
device=gpu,
dtype=torch.bfloat16,
) * 0.01 + init_val
),
requires_grad=True,
)
self.num_params += self.learnable_params[k].numel()
这段代码特别有趣,因为它:
• 仅为 MLP 层创建参数(如果 "mlp" 在 k 中)
• 使用小的高斯噪声(乘以 0.01)加上初始化值进行初始化
• 使用 min(v.shape) 创建向量,使其匹配权重矩阵的较小维度------这很关键,因为 SVD 分解只需要与较小维度相同数量的奇异值
• 采用 bfloat16 精度以提高内存效率
辅助函数 get_soft_mask 是一种平滑阈值机制的实现:
def get_soft_mask(n, fraction):
indices = torch.linspace(0, n - 1, n, dtype=torch.bfloat16) + 1
scaled_indices = indices.to(fraction.device) - fraction * n
result = torch.clamp(scaled_indices, 0, 1)
return 1.0 -- result
这个函数创建了一个连续的掩码,它从 1 平滑过渡到 0,允许参数进行平滑调整,而不是硬性截断。其实现方式:
• 生成均匀分布的索引
• 根据 fraction 参数对其进行缩放
• 将值限制在 0 到 1 之间
• 取反以创建一个从 1 开始并逐渐减少的掩码
策略的掩码生成方法同样重要:
def get_mask(self, p):
return torch.sigmoid(p).to(torch.bfloat16) * self.max_mult
这对学习到的参数应用了 sigmoid 函数,并通过 max_mult 进行缩放,以确保:
• 输出始终为正(由于 sigmoid 的特性)
• 值在合理范围内(由于 max_mult 的限制)
• 梯度流动平稳(由于 sigmoid 的连续性)
该类还包含多个用于参数管理的实用方法:
def get_learnable_params(self, detach=False):
return self.learnable_params
def set_trainable_params_values(self, new_values):
with torch.no_grad():
for p, v in zip(self.trainable_params, new_values):
p.data.copy_(v)
这些方法有助于在前向传播时访问参数,在优化过程中安全更新参数,并管理检查点的状态。
当该策略在主训练循环中使用时,它会生成掩码,以如下方式修改奇异值:
new_param = U @ diag(S * mask) @ V^T * scaling_factor
其中:
• 掩码由策略的 get_mask 方法生成
• U 和 V 是原始的奇异向量
• S 包含奇异值
• scaling_factor 确保修改保持在合理范围内
这是它的代码实现:
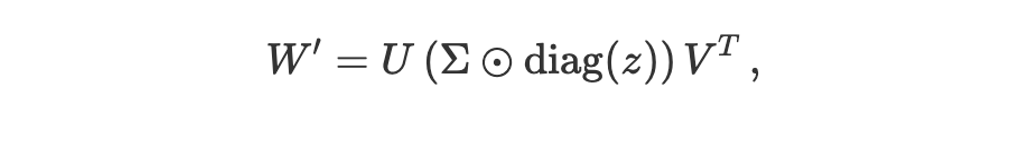
这正是 Transformer² 通过一个小型专家向量 z 仅修改奇异值来"微调"模型的方式。
接下来,policy/weighted_combination.py 扩展了基础 Policy 类,使其能够组合多个专家向量。首先来看初始化部分:
def init(
self,
base_params,
decomposed_params,
base_policy_cfg: Optional[Union[DictConfig, int]],
params_paths: List[str],
gpu,
norm_coeffs,
per_layer,
init_values: Optional[List[float]] = None,
**kwargs,
):
这个复杂的初始化过程处理了多个配置选项,包括:
• 针对不同专家的多个参数路径
• 系数的归一化选项
• 按层适配设置
• 权重的可选初始化值
接下来是专家加载过程:
weights_dict_list: List[Dict[str, torch.Tensor]] = []
if base_policy_cfg is None:
base_policy = Policy(base_params=base_params, gpu=gpu, init_val=0)
elif isinstance(base_policy_cfg, DictConfig):
base_policy: Policy = hydra.utils.instantiate(
base_policy_cfg,
base_params=base_params,
decomposed_params=decomposed_params,
gpu=gpu,
)
这段代码在基础策略初始化方面提供了灵活性,可以创建一个简单的 Policy,或者使用 Hydra 的配置系统 进行更复杂的设置。
专家加载过程继续:
with torch.no_grad():
for i, load_ckpt in enumerate(params_paths):
print(f"Loading checkpoint {i} at {load_ckpt}...")
if "learnable_params" in load_ckpt:
learnable_params = torch.load(load_ckpt)
else:
state_dict = torch.load(load_ckpt, weights_only=True)
base_policy.load_state_dict(state_dict=state_dict)
learnable_params = base_policy.get_learnable_params()
在这里,我们从不同的检查点加载多个专家向量,处理直接的参数文件以及完整的模型状态。
然后,我们初始化自适应权重:
if init_values is None:
init_values = torch.Tensor(
1 / self.num_weights_dict for _ in range(self.num_weights_dict)
)
else:
assert len(init_values) == self.num_weights_dict
init_values = torch.Tensor(init_values)
if per_layer:
self.learned_params_per_weight_dict = self.num_params_per_weight_dict
init_values = torch.stack(
init_values for _ in range(self.learned_params_per_weight_dict)\], dim=1 ) 这段代码: • 如果未提供初始权重,则创建统一的初始值 • 通过 per_layer 标志支持按层适配 • 适当地堆叠权重,以支持全局或按层适配 参数注册过程非常全面: self.parameter_keys = \[
self.original_params = {}
for k, v in weights_dict_list[0].items():
self.parameter_keys.append(k)
self.original_params[k] = []
for i, weight_dict in enumerate(weights_dict_list):
weight_tensor = self.get_mask(p=weight_dict[k])
new_key = k.replace(".", "_")
self.register_buffer(
f"weights_{i}k",
tensor=weight_tensor,
)
这创建了一个结构化的专家参数存储系统,使用 PyTorch 的缓冲区系统进行高效的内存管理。
接下来,我们实现系数生成:
def get_coeff_per_layer(self):
if self.norm:
adaptive_weights = self.adaptive_weights / self.adaptive_weights.sum(0)
else:
adaptive_weights = self.adaptive_weights
weights_per_layer = adaptive_weights.expand(
self.num_weights_dict, self.num_params_per_weight_dict,
)
return weights_per_layer
这个方法:
• 可选地对权重进行归一化,使其总和为 1
• 将权重扩展至涵盖所有层
• 维持高效的张量操作
参数的组合发生在 get_learnable_params 中:
def get_learnable_params(self):
adaptive_coeff_per_layer = self.get_coeff_per_layer()
output_params = {}
for i, (k, vs) in enumerate(self.original_params.items()):
cs_coeff = adaptive_coeff_per_layer[:, i]
out = vs[0] * cs_coeff[0]
for j, other_v in enumerate(vs[1:]):
v_idx = j + 1
out = out + other_v * cs_coeff[v_idx]
output_params[k] = out
这实现了专家向量的加权组合,基于学习到的系数高效地计算参数的线性组合。
最后,是监控系统:
def record_state(self, metrics_to_log):
avg_weights = self.adaptive_weights.mean(-1).detach().cpu().numpy()
dict_to_log = {
f"adaptive_weight/mean_across_params_w{i}": w
for i, w in enumerate(avg_weights.tolist())
}
metrics_to_log.update(**dict_to_log)
这为模型如何组合不同专家提供了关键的可视性,记录了所有参数中每个专家获得的平均权重。
总而言之,policy/base.py 和 weighted_combination.py 定义了专家向量的存储方式、处理方式(例如通过 sigmoid 生成掩码),以及在多个专家存在的情况下,如何将它们组合成最终的修改集。
此外,utils.py 提供了一些关键的辅助函数:
• 从 SVD 组件和学习到的修改中重新组合新的权重矩阵,
• 将这些更新后的参数复制到推理模型(vLLM)中,
• 并促进评估(包括一个两步分类过程,以决定使用哪个专家)。
这些脚本共同实现了对权重矩阵的分解(U, Σ, V^T),然后仅通过轻量级的、学习到的专家向量微调"音量旋钮"(即奇异值),使系统能够快速高效地适应新任务------无需重新训练整个模型。这就是 Transformer² 论文所描述数学理论的实际落地。
Transformer² 的优势
现在让我们放大视角,看看 Transformer² 可能带来的更广泛影响。是什么关键优势让这个框架如此值得关注?为什么我们应该对 LLM 研究的这一新方向感到兴奋?
或许最具吸引力的优势是 效率。在这个扩展 AI 模型通常意味着 计算成本呈指数级增长 的世界里,Transformer² 提供了一种令人耳目一新的解决方案。奇异值微调(Singular Value Fine-tuning,SVF) 的 参数高效特性 是一个颠覆性的变革。通过仅仅调整那些 紧凑的"专家向量" 以微调奇异值,Transformer² 相比传统微调方法,甚至许多 参数高效微调(PEFT) 方法,大幅减少了 可训练参数的数量。想想我们之前的汽车引擎类比------这就像通过调整几个关键设置来优化燃油效率,而不是完全推翻整个发动机设计。这种 高效性 直接转化为 更快的"专家向量"训练、更低的计算开销,以及 潜在的更低存储需求(对于那些专门化的模型)。在 资源受限的环境 或者 需要快速迭代和实验的场景 中,这种 效率优势 可能是一个 关键推动力。
除了 效率 之外,Transformer² 还承诺带来 全新的实时适应能力。两遍推理机制(two-pass inference mechanism) 是这种 动态行为 的核心。它允许 LLM 在第一遍分析输入提示(prompt),然后 在第二遍实时调整权重,彻底改变了 静态微调模型 的局限性。这不再是 为每个任务创建一个单独的专用模型,而是 一个基础模型可以根据当前任务动态调整自身行为。想象一个 AI 助手,它可以 无缝切换 在 编程辅助、数学解题、创意写作 之间,所有这些都在 同一个模型实例中完成,随着你的需求切换,它能够 实时调整"内部齿轮"。这种 动态适应性 可能会 解锁真正交互式和上下文感知的 AI 应用。
此外,Transformer² 还暗示着 更强的通用性和泛化能力。论文的实验结果表明,这一框架 并不局限于特定的 LLM 体系结构。它似乎可以适用于 不同的模型家族(Llama、Mistral),甚至跨越 不同模态,在 视觉-语言任务 上也展现出良好表现。这种 跨架构、跨模态的潜力 令人着迷。它表明 Transformer² 的核心原理------SVF 和动态适应,可能是 一种更基础且广泛适用的方法,而非 仅限于某些特定模型的技术。此外,"专家向量" 的概念也打开了 知识迁移和复用的新可能性。我们是否可以 "移植"在一个模型上训练的专家向量到另一个模型上?或者 将不同领域的专家向量组合在一起,以创建更加 多才多艺且强大的自适应模型?论文在 跨模型迁移(cross-model transfer) 方面的初步实验,已经为这个方向提供了令人鼓舞的证据。
虽然目前的重点主要是 效率和适应性,但论文还 暗示 了 更好的组合性(compositionality)和可解释性(interpretability),尽管这些方面在初步研究中 尚未被充分探索,仍然是 未来研究的方向。专家向量 通过 调节奇异值 作用于 权重矩阵更基础、正交的组成部分,这可能会带来 更模块化和更可解释的适配机制。如果我们能理解 每个专家向量 在 这些奇异成分上具体在"调节"什么,或许可以更 透明地理解 模型如何根据不同任务调整自身行为。然而,这一切 仍然是推测。Transformer² 是否 真的能带来更可解释、更具组合性的模型,还需要 进一步研究和深入分析。
然而,尽管 Transformer² 前景光明,它仍然是 一个相对较新的框架。我们 需要更多研究 来全面理解它的 优劣势。一些 悬而未决的问题和潜在挑战 值得思考:
• 适配策略的复杂性:论文探索了一些 初步的适配策略(基于提示、基于分类器、少样本学习)。那么,如何选择最佳策略 以适应不同任务或应用?我们又该如何设计 更复杂、更加稳健的调度机制,以准确 识别任务特性并选择最合适的专家向量?
• 泛化能力和鲁棒性:尽管 初步结果令人鼓舞,但仍需在 更广泛的任务、数据集和真实世界场景 下评估 Transformer²。它 能否真正泛化 到 全新的、超出训练分布的任务?它在 嘈杂或模糊的输入 下有多 鲁棒?
• 专家向量的扩展性:随着 自适应 LLM 的应用场景越来越多,我们可能需要 训练和管理大量的专家向量,可能多达 成百上千个专门领域。那么,Transformer² 在这种场景下能 如何扩展?是否有 高效的方法来组织、选择、组合庞大的专家向量库?
• 适配速度与性能的权衡:两遍推理机制 相较于 标准推理 引入了一定的 计算开销。尽管论文表明这种 开销是可控的,但我们仍然需要 仔细分析适配速度与性能之间的权衡,特别是在 对延迟要求严格的应用(如实时对话系统)中。
尽管 仍有许多开放性问题,Transformer² 依然展现了 LLM 未来发展的一种极具吸引力的愿景。随着 这一方向的研究不断深入,Transformer² 及其相关的 自适应框架 可能会 彻底改变大型语言模型的格局及其应用方式,让我们拭目以待。
结论
随着我们对 Transformer² 的探索接近尾声,很明显,它不仅仅是 大型语言模型(LLM) 不断进化中的 又一次渐进式改进,而是一种 更根本的变革,甚至可能成为 LLM 适配方式的范式转变。它大胆设想了一个未来,在这个未来里,我们或许 不再需要传统意义上的"微调",而是直接采用 天生更加动态和响应迅速的模型。
其 核心创新,正如我们之前解析的,体现在 奇异值微调(SVF) 和 两遍推理机制 的 优雅结合。SVF 通过 参数高效的方式,仅调节奇异值,提供了一种 相较于传统微调更具吸引力的替代方案,避免了 计算资源消耗大且往往静态不变的传统微调方法。同时,两遍推理机制 赋予了 LLM 更强的自适应能力,使其能够在 第一遍分析输入需求后,第二遍动态调整自身权重,以 实时适应任务的需求。
Transformer² 的 潜在优势 不容忽视:
• 更高的效率,有望 降低计算成本 并 加快适配周期;
• 真正的实时适应能力,意味着 LLM 可以在不同任务间无缝切换,而无需显式重新训练;
• 更广泛的适用性,表明它不仅适用于 不同的 LLM 体系结构,甚至可能扩展到 多模态任务。
这些优势不仅仅是 渐进式改进,而是指向了一种 本质上不同的 AI------它 不再只是单一任务的工具集合,而是 一种真正通用的智能系统,能够 动态调整自己的能力,适应 不同任务需求。
当然,我们必须认识到,Transformer² 仍然处于 相对早期的发展阶段。仍有 许多未解的问题,需要 进一步研究 来 充分挖掘其潜力,并解决其局限性。例如:
• 最优的适配策略:目前论文探讨了 基于提示、基于分类器、少样本学习等方法,但如何 选择最适合特定任务的策略?我们能否设计出 更复杂、更健壮的调度机制 来 识别任务需求并选择合适的专家向量?
• 泛化能力与鲁棒性:Transformer² 在 更广泛的任务、数据集和真实世界场景 下的表现如何?它 能否真正泛化到从未见过的任务?面对 嘈杂或模糊的输入,它是否 足够稳健?
• 可扩展性:如果 未来 LLM 需要处理数百甚至数千个不同的专家向量,Transformer² 能否 有效管理和组织如此庞大的专家库?
• 适配速度与性能的权衡:两遍推理机制 相较于 标准推理 会引入一定 额外开销。尽管论文表明 这种开销可控,但我们仍然需要 进一步分析在低延迟应用场景下的实际影响。
尽管仍有 许多开放问题,但 Transformer² 仍然提供了 一个极具价值且鼓舞人心的蓝图。它 挑战了我们对 LLM 适配方式的传统认知,让我们 摆脱静态微调的局限,去探索 自适应 AI 系统的全新可能性。无论 Transformer² 本身最终 是否会成为主流范式,还是只是 迈向更高级自适应框架的垫脚石,有一点已经 越来越清晰:
真正的、可动态适配的 LLM 之旅才刚刚开始,这将是一场令人兴奋且充满变革的旅程。
参考文献
Qi Sun, et al. "TRANSFORMER-SQUARED: SELF-ADAPTIVE LLMS". [arXiv 链接: http://arxiv.org/abs/2501.06252v3].