图的储存+图的遍历

图的存储

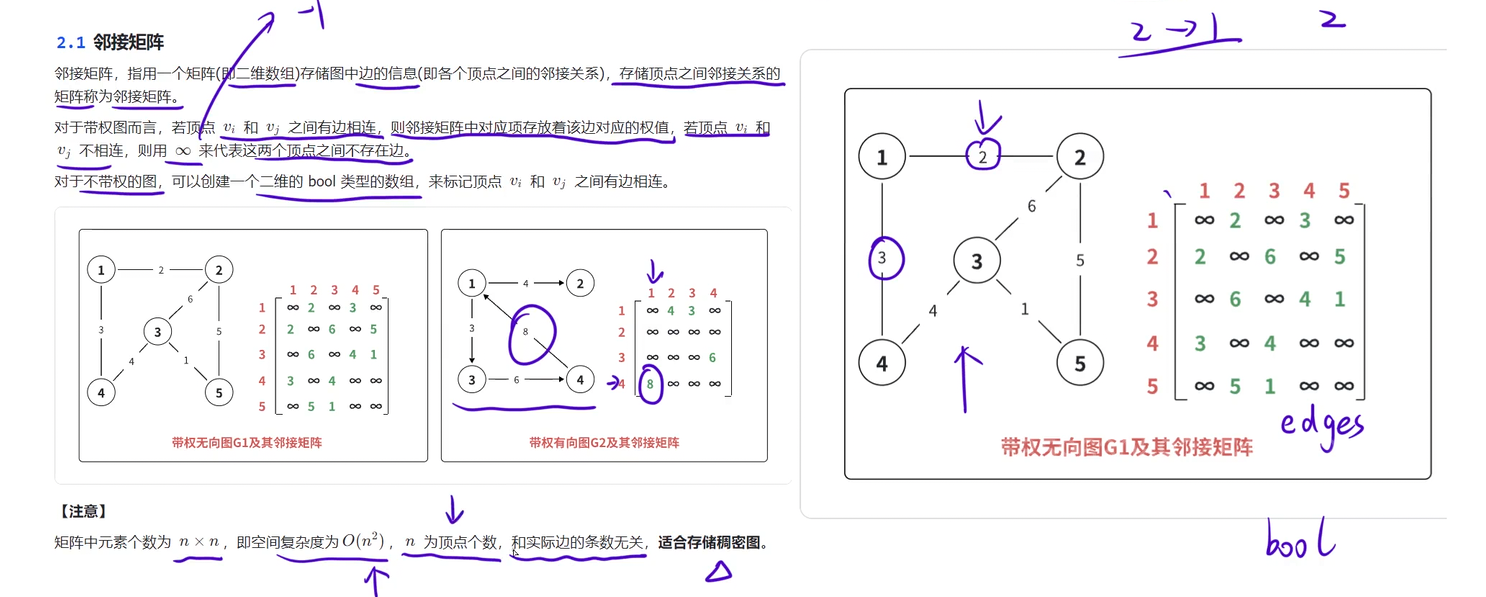
邻接矩阵

cpp 复制代码

#include <iostream>

#include <cstring>

using namespace std;

const int N = 1010;

int n, m;

int edges[N][N];

int main()
{
 memset(edges, -1, sizeof edges);
 cin >> n >> m; // 读⼊结点个数以及边的个数 
 for(int i = 1; i <= m; i++)
 {
 int a, b, c; cin >> a >> b >> c; 
 // a - b 有⼀条边，权值为 c 
 edges[a][b] = c;
 // 如果是⽆向边，需要反过来再存⼀下 
 edges[b][a] = c;
 }
return 0;
}

邻接表

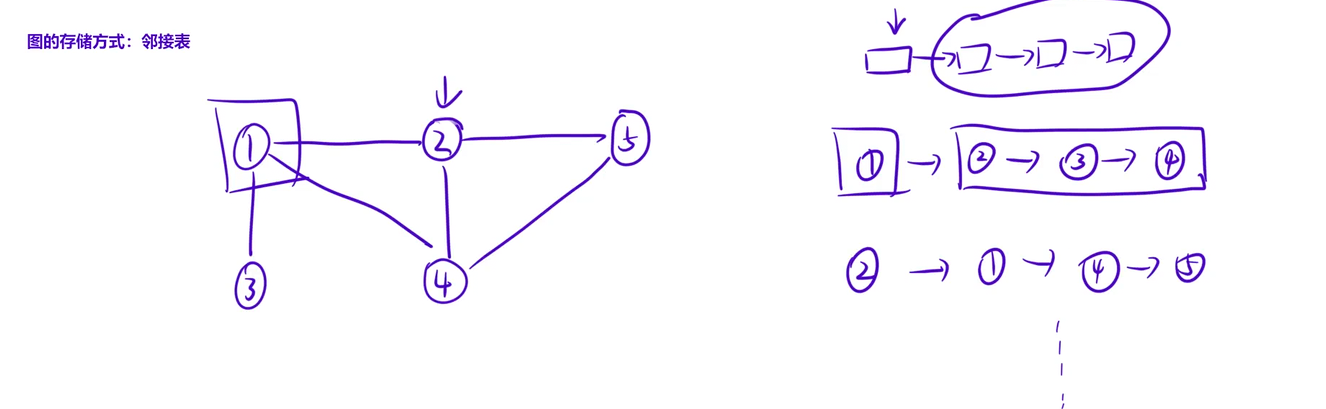
和树的存储⼀模⼀样，只不过如果存在边权的话，我们的vector数组⾥⾯放⼀个结构体或者是pair即可。

cpp 复制代码

#include <iostream>

#include <vector>

using namespace std;

typedef pair<int, int> PII;//那个结点，权值

const int N = 1e5 + 10;

int n, m;
vector<PII> edges[N];

int main()
{
 cin >> n >> m; // 读⼊结点个数以及边的个数 
 for(int i = 1; i <= m; i++)
 {
 int a, b, c; cin >> a >> b >> c;
 // a 和 b 之间有⼀条边，权值为 c 
 edges[a].push_back({b, c});
 
 // 如果是⽆向边，需要反过来再存⼀下 
 edges[b].push_back({a, c});
 }
 return 0;
}

链式前向星

和树的存储⼀模⼀样，只不过如果存在边权的话，我们多创建⼀维数组，⽤来存储边的权值即可。

cpp 复制代码

#include <iostream>

using namespace std;

const int N = 1e5 + 10;

// 链式前向星 

int h[N], e[N * 2], ne[N * 2], w[N * 2], id;

int n, m;

// 其实就是把 b 头插到 a 所在的链表后⾯ 

void add(int a, int b, int c)
{
 id++;
 e[id] = b;
 w[id] = c; // 多存⼀个权值信息 
 ne[id] = h[a];
 h[a] = id;
}

int main()
{
 cin >> n >> m; // 读⼊结点个数以及边的个数 
 for(int i = 1; i <= m; i++)
 {
 int a, b, c; cin >> a >> b >> c;
 // a 和 b 之间有⼀条边，权值为 c 
 add(a, b, c); add(b, a, c);
 }
 return 0;
}

图的遍历

dfs

1.邻接矩阵

cpp 复制代码

#include <iostream>

#include <cstring>

#include <queue>

using namespace std;

const int N = 1010;

int n, m;

int edges[N][N];

bool st[N]; // 标记哪些点已经访问过 

void dfs(int u)
{
 cout << u << endl;
 st[u] = true;
 // 遍历所有孩⼦ 
 for(int v = 1; v <= n; v++)
 {
 // 如果存在 u->v 的边，并且没有遍历过 
 if(edges[u][v] != -1 && !st[v])
 {
 dfs(v);
 }
 }
}

int main()
{
 memset(edges, -1, sizeof edges);
 cin >> n >> m; // 读⼊结点个数以及边的个数 
 for(int i = 1; i <= m; i++)
 {
 int a, b, c; cin >> a >> b >> c; 
 // a - b 有⼀条边，权值为 c 
 edges[a][b] = c;
 // 如果是⽆向边，需要反过来再存⼀下 
 edges[b][a] = c;
 }
 return 0;
}

2.vector数组

cpp 复制代码

#include <iostream>

#include <vector>

#include <queue>

using namespace std;

typedef pair<int, int> PII;

const int N = 1e5 + 10;

int n, m;
vector<PII> edges[N];

bool st[N]; // 标记哪些点已经访问过 

void dfs(int u)
{
 cout << u << endl;
 st[u] = true;
 // 遍历所有孩⼦ 
 for(auto& t : edges[u])
 {
 // u->v 的⼀条边，权值为 w 
 int v = t.first, w = t.second;
 if(!st[v]) 
 {
 dfs(v);
 }
 }
}

int main()
{
 cin >> n >> m; // 读⼊结点个数以及边的个数 
 for(int i = 1; i <= m; i++)
 {
  int a, b, c; cin >> a >> b >> c;
 // a 和 b 之间有⼀条边，权值为 c 
 edges[a].push_back({b, c});
 
 // 如果是⽆向边，需要反过来再存⼀下 
 edges[b].push_back({a, c});
 }
 return 0;
}

bfs

邻接矩阵

cpp 复制代码

#include <iostream>

#include <cstring>

#include <queue>

using namespace std;

const int N = 1010;

int n, m;

int edges[N][N];

1
2
3
4
5
6
7
8
9
10
bool st[N]; // 标记哪些点已经访问过 

void bfs(int u)
{
 queue<int> q;
 q.push(u);
 st[u] = true;
 while(q.size())
 {
 auto a = q.front(); q.pop();
 cout << a << endl;
 for(int b = 1; b <= n; b++)
 {
 if(edges[a][b] != -1 && !st[b])
 {
 q.push(b);
 st[b] = true;
 }
 }
 }
}

int main()
{
 memset(edges, -1, sizeof edges);
 cin >> n >> m; // 读⼊结点个数以及边的个数 
 for(int i = 1; i <= m; i++)
 {
 int a, b, c; cin >> a >> b >> c; 
 // a - b 有⼀条边，权值为 c 
 edges[a][b] = c;
 // 如果是⽆向边，需要反过来再存⼀下 
 edges[b][a] = c;
 }
 return 0;
}

vector数组

cpp 复制代码

#include <iostream>

#include <vector>

#include <queue>

using namespace std;

typedef pair<int, int> PII;

const int N = 1e5 + 10;

int n, m;
vector<PII> edges[N];

bool st[N]; // 标记哪些点已经访问过 

void bfs(int u)
{
 queue<int> q;
 q.push(u);
 st[u] = true;
 while(q.size())
 {
 auto a = q.front(); q.pop();
 cout << a << endl;
 for(auto& t : edges[a])
 {
 int b = t.first, c = t.second;
 if(!st[b])
 {
 q.push(b);
 st[b] = true;
 }
 }
 }
}

int main()
{
 cin >> n >> m; // 读⼊结点个数以及边的个数 
 for(int i = 1; i <= m; i++)
 {
 int a, b, c; cin >> a >> b >> c;
 // a 和 b 之间有⼀条边，权值为 c 
 edges[a].push_back({b, c});
 
 // 如果是⽆向边，需要反过来再存⼀下 
 edges[b].push_back({a, c});
 }
 return 0;
}