- 什么是单调栈?
单调栈,顾名思义,就是具有单调性的栈。它依旧是⼀个栈结构,只不过⾥⾯存储的数据是递增或者递减的。这种结构是很容易实现的(如下⾯的代码),但重点是维护⼀个单调栈的意义是什么
c++
#include <iostream>
#include <stack>
using namespace std;
const int N = 3e6 + 10;
int a[N], n;
void test1()
{
stack<int> st; // 维护⼀个单调递增的栈
for(int i = 1; i <= n; i++)
{
// 栈⾥⾯⼤于等于 a[i] 的元素全部出栈
while(st.size() && st.top() >= a[i]) st.pop();
st.push(a[i]);
}
}
void test2()
{
stack<int> st; // 维护⼀个单调递减的栈
for(int i = 1; i <= n; i++)
{
// 栈⾥⾯⼩于等于 a[i] 的元素全部出栈
while(st.size() && st.top() <= a[i]) st.pop();
st.push(a[i]);
}
}- 单调栈解决的问题
单调栈能帮助我们解决以下四个问题:
- 寻找当前元素左侧,离它最近,并且⽐它⼤的元素在哪;
- 寻找当前元素左侧,离它最近,并且⽐它⼩的元素在哪;
- 寻找当前元素右侧,离它最近,并且⽐它⼤的元素在哪;
- 寻找当前元素右侧,离它最近,并且⽐它⼩的元素在哪。
虽然是四个问题,但是原理是⼀致的。因此,只要解决⼀个,举⼀反三就可以解决剩下的⼏个
- 寻找当前元素左侧,离它最近,并且⽐它⼤的元素在哪
从左往右遍历元素,构造⼀个单调递减的栈。插⼊当前位置的元素的时:
- 如果栈为空,则左侧不存在⽐当前元素⼤的元素;
- 如果栈⾮空,插⼊当前位置元素时的栈顶元素就是所找的元素。
注意,因为我们要找的是最终结果的位置。因此,栈⾥⾯存的是每个元素的下标
c++
输⼊:
9 1
4 10 6 3 3 15 21 8
输出:
0 0 0 3 4 4 0 0 8
c++
#include <iostream>
#include <stack>
using namespace std;
const int N = 3e6 + 10;
int a[N], n;
int ret[N];
void test()
{
stack<int> st; // 维护⼀个单调递减的栈
for(int i = 1; i <= n; i++)
{
// 栈⾥⾯⼩于等于 a[i] 的元素全部出栈
while(st.size() && a[st.top()] <= a[i]) st.pop();
// 此时栈顶元素存在,栈顶元素就是所求结果
if(st.size()) ret[i] = st.top();
st.push(i); // 存的是下标
}
for(int i = 1; i <= n; i++)
{
cout << ret[i] << " ";
}
cout << endl;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
test(); cout << endl;
return 0;
}- 寻找当前元素左侧,离它最近,并且⽐它⼩的元素在哪
从左往右遍历元素,构造⼀个单调递增的栈。插⼊当前位置的元素的时:
- 如果栈为空,则左侧不存在⽐当前元素⼩的元素;
- 如果栈⾮空,插⼊当前位置元素时的栈顶元素就是所找的元素。
注意,因为我们要找的是最终结果的位置。因此,栈⾥⾯存的是每个元素的下标
c++
输⼊:
9 1
4 10 6 3 3 15 21 8
输出:
0 1 2 2 1 1 6 7 6
c++
#include <iostream>
#include <stack>
using namespace std;
const int N = 3e6 + 10;
int a[N], n;
int ret[N];
void test()
{
stack<int> st; // 维护⼀个单调递增的栈
for(int i = 1; i <= n; i++)
{
// 栈⾥⾯⼤于等于 a[i] 的元素全部出栈
while(st.size() && a[st.top()] >= a[i]) st.pop();
// 此时栈顶元素存在,栈顶元素就是所求结果
if(st.size()) ret[i] = st.top();
st.push(i); // 存的是下标
}
for(int i = 1; i <= n; i++)
{
cout << ret[i] << " ";
}
cout << endl;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
test(); cout << endl;
return 0;
}针对其余两种情况,我们仅需逆序遍历数组即可。
- 寻找当前元素右侧,离它最近,并且⽐它⼤的元素在哪
从右往左遍历元素,构造⼀个单调递减的栈。插⼊当前位置的元素的时:
- 如果栈为空,则左侧不存在⽐当前元素⼤的元素;
- 如果栈⾮空,插⼊当前位置元素时的栈顶元素就是所找的元素。
注意,因为我们要找的是最终结果的位置。因此,栈⾥⾯存的是每个元素的下标
c++
输⼊:
9 1
4 10 6 3 3 15 21 8
输出:
2 3 7 7 7 7 8 0 0
c++
#include <iostream>
#include <stack>
using namespace std;
const int N = 3e6 + 10;
int a[N], n;
int ret[N];
void test()
{
stack<int> st; // 维护⼀个单调递减的栈
for(int i = n; i >= 1; i--)
{
// 栈⾥⾯⼩于等于 a[i] 的元素全部出栈
while(st.size() && a[st.top()] <= a[i]) st.pop();
// 此时栈顶元素存在,栈顶元素就是所求结果
if(st.size()) ret[i] = st.top();
st.push(i); // 存的是下标
}
for(int i = 1; i <= n; i++)
{
cout << ret[i] << " ";
}
cout << endl;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
test(); cout << endl;
return 0;
}- 寻找当前元素右侧,离它最近,并且⽐它⼩的元素在哪
从右往左遍历元素,构造⼀个单调递增的栈。插⼊当前位置的元素的时:
- 如果栈为空,则左侧不存在⽐当前元素⼩的元素;
- 如果栈⾮空,插⼊当前位置元素时的栈顶元素就是所找的元素。
注意,因为我们要找的是最终结果的位置。因此,栈⾥⾯存的是每个元素的下标
c++
输⼊:
9 1
4 10 6 3 3 15 21 8
输出:
0 5 4 5 0 0 9 9 0
c++
#include <iostream>
#include <stack>
using namespace std;
const int N = 3e6 + 10;
int a[N], n;
int ret[N];
void test()
{
stack<int> st; // 维护⼀个单调递增的栈
for(int i = n; i >= 1; i--)
{
// 栈⾥⾯⼤于等于 a[i] 的元素全部出栈
while(st.size() && a[st.top()] >= a[i]) st.pop();
// 此时栈顶元素存在,栈顶元素就是所求结果
if(st.size()) ret[i] = st.top();
st.push(i); // 存的是下标
}
for(int i = 1; i <= n; i++)
{
cout << ret[i] << " ";
}
cout << endl;
}
int main()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
test(); cout << endl;
return 0;
}- 找左侧,正遍历;找右侧,逆遍历;
- ⽐它⼤,单调减;⽐它⼩,单调增。
P5788 【模板】单调栈 - 洛谷
右侧离它最近并且⽐它⼤的元素:
- 逆序遍历数组;
- 构造⼀个单调递减的栈;
- 进栈时,栈顶元素就是最终结果
c++
#include <bits/stdc++.h>
using namespace std;
const int N = 3e6 + 10;
int n;
int a[N];
int ret[N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) cin >> a[i];
stack<int> st;
for (int i = n; i >= 1; i--)
{
while (st.size() && a[st.top()] <= a[i]) st.pop();
if (st.size()) ret[i] = st.top();
st.push(i);
}
for (int i = 1; i <= n; i++) cout << ret[i] << " ";
cout << endl;
return 0;
}P1901 发射站 - 洛谷
c++
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e6 + 10;
int n;
LL h[N], v[N];
LL sum[N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
cin >> n;
for (int i = 1; i <= n; i++) cin >> h[i] >> v[i];
//找左边
stack<int> st;
for (int i = 1; i <= n; i++)
{
//递减栈
while (st.size() && h[st.top()] <= h[i]) st.pop();
if (st.size())
{
sum[st.top()] += v[i];
}
st.push(i);
}
//找右边
while (st.size()) st.pop(); //清空
for (int i = n; i >= 1; i--)
{
//递减栈
while (st.size() && h[st.top()] <= h[i]) st.pop();
if (st.size())
{
sum[st.top()] += v[i];
}
st.push(i);
}
LL ret = 0;
for (int i = 1; i <= n; i++) ret = max(ret, sum[i]);
cout << ret << endl;
return 0;
}SP1805 HISTOGRA - Largest Rectangle in a Histogram - 洛谷
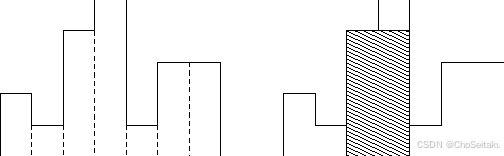
对于x位置⼦矩阵,找到左侧离它最近并且⽐它⼩的位置y ,那么[x+1, y]之间就是该矩阵能到达的左端。
同理再找到右侧离它最近并且⽐它⼩的位置z ,那么[y, z - 1]之间就是该矩阵能到达的右端。
对于每⼀个⼦矩阵,求出它向左以及向右能延伸的最⼤⻓度即可
c++
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 1e5 + 10;
int n;
LL h[N];
LL x[N], y[N];
int main()
{
ios::sync_with_stdio(false);
cin.tie(0);
while (cin >> n, n)
{
for (int i = 1; i <= n; i++) cin >> h[i];
//找左边
stack<int> st;
for (int i = 1; i <= n; i++)
{
//单调递增栈
while (st.size() && h[st.top()] >= h[i]) st.pop();
if (st.size()) x[i] = st.top();
else x[i] = 0;
st.push(i);
}
//找右边
while (st.size()) st.pop();
for (int i = n; i >= 1; i--)
{
//单调递增栈
while (st.size() && h[st.top()] >= h[i]) st.pop();
if (st.size()) y[i] = st.top();
else y[i] = n + 1;
st.push(i);
}
LL ret = 0;
for (int i = 1; i <= n; i++)
{
ret = max(ret, h[i] * (y[i] - x[i] - 1));
}
cout << ret << endl;
}
return 0;
}