神经网络与模型训练过程笔记

1.专有名词

ANN

人工神经网络，一种受生物神经元启发的监督学习算法。输入数据通过网络中的层级函数传递 ，激活特定神经元。函数复杂度越高，模型对数据的拟合能力越强，预测精度越高。

偏置项

其中x下表从1开始的是输入变量，下标为0的是偏置项，从1开始的都是权重。

前向传播

前向传播是神经网络的核心计算过程，指输入数据从输入层 逐层传递到输出层的路径。其目的是通过网络的权重和激活函数，计算最终的预测输出。

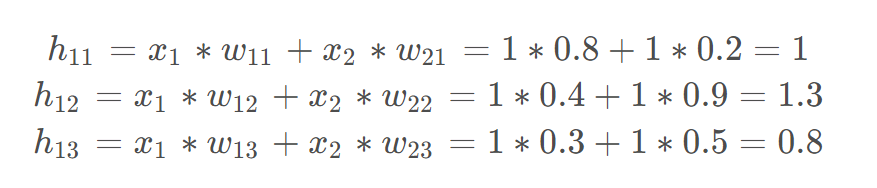
如果隐藏层没有非线性激活函数，那么输入和输出是线性关系的。

激活函数

激活函数是神经网络的核心组件，用于引入非线性，使网络能够拟合复杂的数据模式。如果没有激活函数，神经网络将退化为线性回归模型。

假如激活函数为Sigmoid函数。

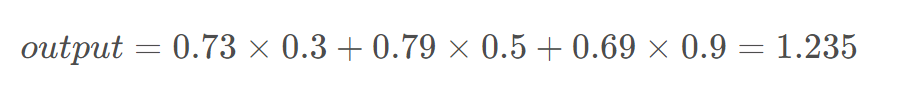
损失值

损失值是神经网络训练的核心指标，用于衡量模型预测结果与真实值之间的差异。通过最小化损失值，模型逐步优化参数，提升预测精度。

连续变量预测过程中计算损失值

其中，实际输出，是由神经网络(权重为)得到的预测输出，输入，m为训练的样本数。

假设上面的图预测的是连续变量。

离散变量预测过程中计算损失值

二元交叉熵

分类交叉熵

反向传播

反向传播是"反着来"的过程，用于根据损失函数对各个权重进行微调。
关键步骤：
1. 每次只对网络中每个权重做一点点修改（微调）
2. 测量在权重变化()时，损失值（Loss）的变化()情况（偏导数）
3. 使用学习率 k控制更新步长：

学习率

是一个控制每次更新步幅的超参数。太大容易发散，太小学习慢。有助于在训练时稳定地下降损失函数，使模型最终达到最优或近似最优的状态。

epoch

所有数据被重复用于训练若干次，每一次完整地训练整个数据集叫做一个 epoch。

梯度下降

更新权重以减少误差值的整个过程称为梯度下降。

实现向前传播

python 复制代码

import numpy as np

def feed_forward(inputs, outputs, weights):
    # 计算隐藏层的加权输入：inputs 与隐藏层权重 weights[0] 做点积，加上偏置 weights[1]
    pre_hidden = np.dot(inputs, weights[0]) + weights[1]
    
    # 使用 sigmoid 激活函数对隐藏层加权输入进行非线性变换
    hidden = 1 / (1 + np.exp(-pre_hidden))
    
    # 计算输出层的加权输入：隐藏层输出与输出层权重 weights[2] 做点积，加上偏置 weights[3]
    pred_out = np.dot(hidden, weights[2]) + weights[3]
    
    # 计算预测输出与实际输出之间的均方误差（MSE）
    mean_squared_error = np.mean(np.square(pred_out - outputs))
    
    # 返回均方误差作为损失值
    return mean_squared_error

输入特征 → 加权求和 → 加上偏置
进入隐藏层（激活函数变换）
再次加权 → 输出预测结果
比较预测值和真实值 → 得到损失

实现梯度下降算法

python 复制代码

from copy import deepcopy

# 更新神经网络的权重
def update_weights(inputs, outputs, weights, lr):
    """
    使用数值梯度下降法更新神经网络的权重。
    
    enumerate()，用来在遍历可迭代对象（如列表、元组）时，同时获取元素的索引和值。

    参数：
    inputs  ------ 输入数据，形状为 (样本数, 输入特征数)
    outputs ------ 真实标签，形状为 (样本数, 输出特征数)
    weights ------ 当前神经网络的权重列表（包含4个部分）
    lr      ------ 学习率（learning rate），控制更新步长

    返回：
    updated_weights ------ 更新后的权重
    original_loss   ------ 更新前的损失（MSE）
    """

    original_weights = deepcopy(weights)     # 保存原始权重（不修改）
    temp_weights = deepcopy(weights)         # 用于临时尝试修改某个权重
    updated_weights = deepcopy(weights)      # 保存最终更新后的权重

    original_loss = feed_forward(inputs, outputs, original_weights)  # 当前权重下的损失

    # 遍历每一层的权重（共4个部分：输入到隐藏权重、隐藏偏置、隐藏到输出权重、输出偏置）
    for i, layer in enumerate(original_weights):
        # 遍历当前层中的每个元素（权重或偏置）
        for index, weight in np.ndenumerate(layer):
            temp_weights = deepcopy(weights)  # 复制当前权重
            temp_weights[i][index] += 0.0001  # 对当前权重增加一个微小扰动（用于计算导数）

            _loss_plus = feed_forward(inputs, outputs, temp_weights)  # 计算扰动后新的损失

            # 使用数值导数公式估计梯度：grad ≈ (L(w+ε) - L(w)) / ε
            grad = (_loss_plus - original_loss) / (0.0001)

            # 用梯度下降法更新当前权重：w = w - lr * grad
            updated_weights[i][index] -= grad * lr

    return updated_weights, original_loss