ECMAScript 杂谈：再谈数值

前言

ECMAScript标准是深入学习JavaScript原理最好的资料，没有其二。

通过增加对ECMAScript语言的理解，理解javascript现象后面的逻辑，提升个人编码能力。

欢迎关注和订阅专栏重学前端-ECMAScript协议上篇

准备

安装node之后，可以使用命令： node --allow-natives-syntax xxx.js

--allow-natives-syntax 选项开启之后，可以使用v8的一些内部方法，比如%DebugPrint可以输出对象的调试信息。

字符串转为数值

作为前端开发，难免会遇到需要把字符串转为数字的情况，接下来就说说常用的方法。

转为浮点数 `parseFloat`

使用parseFloat或者 Number.parseFloat均可。

首位的空白字符会忽略
Infinity 和字符串的 Infinity可以被解析
可以解析科学计数法
解析BigInt可能不准

javascript 复制代码

parseFloat(' 100.x    ') // 100

parseFloat(Infinity);       // Infinity
parseFloat('Infinity');     // Infinity
parseFloat(-Infinity);      // -Infinity
parseFloat('-Infinity');    // -Infinity

parseFloat('100.x')      // 100
parseFloat('1e29')       // 1e29

parseFloat(900719925474099267n);     // 900719925474099300
parseFloat('900719925474099267n')    // 900719925474099300

转为整数 `parseInt`

使用parseInt或者 Number.parseInt均可。

语法： Number.parseInt(string, radix)

需要注意的一点就是radix，基数小于 2 或大于 36，或第一个非空白字符不能转换为数字，则返回 NaN.

javascript 复制代码

parseInt('123x')   // 123
parseInt('a', 16)  // 10

一个有意思的场景, 至于答案，自行思考。

javascript 复制代码

[1,2,3].map(parseInt)

简单解析一下：

map 的回调函数有多个参数, function(element, index, array){ /* ... */ }
radix的取值范围是 2-36，假如 radix 未指定或者为 0，除非数字以 0x 或 0X 开头（此时假定为十六进制 16），否则假定为 10（十进制）。

javascript 复制代码

[1,2,3].map(parseInt)   // [1, NaN, NaN]
// 等同于 [parseInt(1, 0),parseInt(2, 1), parseInt(3, 2)]
// 等同于 [parseInt(1, 10),parseInt(2, 1), parseInt(3, 2)]

使用一元 + 转为数值

如果是浮点数在 Number.MAX_VALUE和 Number.MIN_VALUE 之间，那么是安全的。其也能识别科学计算法。

如果是整数在 Number.MAX_SAFE_INTEGER和 Number.MIN_SAFE_INTEGER之间的值，也是安全的。

至于为什么，Unary + Operator其底层调用的是 ToNumber，应该能给你一些提示信息。

javascript 复制代码

+ '23'                       // 23
+ ' -456'                    // -456
+'9007199254740995'          // 9007199254740996
+ '1.7976931348623157e+308'  // 1.7976931348623157e+308

细心的同学都发现，最后+'9007199254740995'的结果已经出现误差。

所以确保的你的值是数值，且是 安全范围内 的数值，使用 + x 真的就是非常简单的转换方式。

使用位移转为数值

最常用的手段就是 >> 0,没错，就是右移0位，移动0位本身数值不会变化，借用的是 >>符号，会把操作数转为32位整数的骚操作。

成也32位，败也32位，因为这个限制，超过32位的，那么就会不准确。

具体细节可以参考 JavaScript中奇特的~运算符。

前端用的一般是有符号数值，根据ECMAScript 协议，其底层其实调用的是 Number::signedRightShift ( x, y )

其中的 x就是需要被转换的值，所以确保的你的数值是安全的数值。

javascript 复制代码

'-123456'  >> 0    // -123456
'4294967396' >> 0  // 100

这种方法有一个好处，它是相对安全的， BigInt和未定义等特殊情况除外。

javascript 复制代码

(null) >> 0   // 0
(NaN) >> 0    // 0
({a:1}) >> 0  // 0


xxxx  >> 0    // Uncaught ReferenceError: xxxx is not defined
100n >> 0     // Uncaught TypeError: Cannot mix BigInt and other types, use explicit conversions

0 和 -0

区别 0 和 -0

这两个是同一个玩意吗？

javascript 复制代码

0 === -0         // true
Object.is(0,-0)  // false

虽然值比较返回是true，使用Object.is比较，返回是false。很好，不是一个玩意。

Object.is 是怎么实现的呢？在此之前，先看看ECMASCript协议里面两个方法, 很重要，值比较的时候，高频出现。

7.2.10 SameValue ( x, y ) 和 7.2.11 SameValueZero ( x, y )

SameValueZero和SameValue的唯一区别在于前者把0和-0认为是等同的。为啥要搞这么复杂，当然也会对应着ES对应的方法，再看两张截图：

没错，Object.is 内部调用的是SameValue， Array, Map和Set 的includes 内部调用的SameValueZero, 所以你感觉不到+0和-0。

看完协议，就可以根据协议手写Object.is, 不过，你要是按照协议写，估计得累死。

判断两个参数x,y的类型，如果不同返回false
如果x是数字，调用 Number:sameValue
调用 SameValueNonNumberic
1. 如果 x 是 null或者undefined，返回 true
2. 如果x 是 BigInt，.....
3. 如果x是字符串，......
4. 如果x是 Boolean，......
5. 如果 x 是 y，返回 true

当然，core-js 提供了非常简洁的实现 same-value.js

javascript 复制代码

// `SameValue` abstract operation
// https://tc39.es/ecma262/#sec-samevalue
// eslint-disable-next-line es/no-object-is -- safe
module.exports = Object.is || function is(x, y) {
  // eslint-disable-next-line no-self-compare -- NaN check
  return x === y ? x !== 0 || 1 / x === 1 / y : x !== x && y !== y;
};

其思路是先严格比较，然后再单独判断 -0 和0 （1/0 => Infinity, 1/-0 => -Infinity）， NaN （自身不等于自身）两种特殊情况。

有模学样，是单单判断是不是 +0，可以简化方法

javascript 复制代码

function isPositiveZero(x){
  return x === 0 && 1 / x > 0;
}

Smi 和 HEAP_NUMBER_TYPE

node版本 v16.10.0 64位

表象看完，继续深入，一起看看调试信息：

javascript 复制代码

%DebugPrint(0);
%DebugPrint(-0);

javascript 复制代码

DebugPrint: Smi: 0x0 (0)

DebugPrint: 0.0
0000014D28B815C9: [Map] in ReadOnlySpace
 - type: HEAP_NUMBER_TYPE
 - instance size: 16
 - elements kind: HOLEY_ELEMENTS
 - unused property fields: 0
 - enum length: invalid
 - stable_map
 - back pointer: 0x014d28b81599 <undefined>
 - prototype_validity cell: 0
 - instance descriptors (own) #0: 0x014d28b81249 <Other heap object (STRONG_DESCRIPTOR_ARRAY_TYPE)>
 - prototype: 0x014d28b81319 <null>
 - constructor: 0x014d28b81319 <null>
 - dependent code: 0x014d28b81239 <Other heap object (WEAK_FIXED_ARRAY_TYPE)>
 - construction counter: 0

注意第一次输出的 Smi，

注意第二次数次的 type: HEAP_NUMBER_TYPE。

都是数字，但是v8内部是做了区分的。

再看一组数据，你可能会更好的了解

javascript 复制代码

%DebugPrint(56);              // Smi
%DebugPrint(-56);             // Smi
%DebugPrint(2**30);           // Smi
%DebugPrint(-(2**30));        // Smi
%DebugPrint(0);               // Smi

console.log("------------------");
%DebugPrint(-Infinity);       // HEAP_NUMBER_TYPE
%DebugPrint(-(2**31)-1);      // HEAP_NUMBER_TYPE
%DebugPrint(        -0);      // HEAP_NUMBER_TYPE
%DebugPrint(     56.56);      // HEAP_NUMBER_TYPE
%DebugPrint(  Infinity);      // HEAP_NUMBER_TYPE
%DebugPrint(       NaN);      // HEAP_NUMBER_TYPE

大致可以得出：

Smi类型：小整数
0， -(2**31) <= x < 2**31
HEAP_NUMBER_TYPE： Infinity， -Infinity，小数，小于 -2**31或者大于等于 2**31

那这有啥区别吗，细节嘛，得去品位v8的代码，表象可以测试一番， Smi的操作速度会更快一些。

进行 100010001000的运算

javascript 复制代码

var num1 = 0;
var num2 = -0;


const count = 1000 * 1000 * 1000;
const startTime = performance.now();

for (let i = 0; i < count; i++) {
    num1 += 1
}

// for (let i = 0; i < count; i++) {
//     num2 += 1
// }

console.log("cost:", performance.now() - startTime)

本机的测试结果：

0的三次运行结果

-0的三次运行结果

小手一抖，30%有没有，不要较真，有一缕意思就行。

NaN

你说这玩意，是数字吧，其全称为 Not A Number, 表示自己不是一个数字，可是身体很老实，typeof NaN 返回的是 number。

特点

typeof的返回值是 number
严等比较自己不等于自己
不可以被改写（现代浏览器）

javascript 复制代码

typeof NaN  // number
NaN === NaN  // false

至于第三个特点，NaN本质是全局对象上的一个属性，并且不可以被配置，被改写。千万别问configurable和writable是什么意思，问也是白问。

精准识别

换做以往，要怎么识别NaN呢？

javascript 复制代码

function isNaNVal(val){
    return typeof val === 'number' && isNaN(val)
}

现在嘛 Object.is和Number.isNaN都可以轻松裁定。

javascript 复制代码

var nanVal = NaN;
Object.is(nanVal, NaN)  // true
Number.isNaN(nanVal);   // true

数组includes注意

Array.prototype.indexOf和Array.prototype.includes都可以查询某个值是否在数组中，表面看起来一个返回的是数字，一个返回的是布尔值。

javascript 复制代码

var arr = [1,2,3,NaN];
arr.indexOf(2)  // 1
arr.includes(2) // true

貌似没有问题，但是NaN是个特例, indexOf检测不出NaN。

javascript 复制代码

var arr = [1,2,3,NaN];
arr.indexOf(NaN)  // -1
arr.includes(NaN) // true

至于为什么这样？

Array.prototype.includes 在比较数值时，使用的 Number::sameValueZero ( x, y )，都是NaN时返回了true。

Array.prototype.indexOf 在比较数值时，使用的是 Number::equal ( x, y )，任何一个值是NaN就已经返回false

Number.isInteger

Number.isInteger可以判断一个数字是不是整数，但是吗，凡事有些意外。

javascript 复制代码

Number.isInteger(3);                  // true
Number.isInteger(  3.000000000000002)   // false
Number.isInteger(  3.0000000000000002)  // true

Number.isInteger( 13.000000000000002)  // false
Number.isInteger(130.000000000000002)  // true

3.000000000000002.toString(2)  // 11.000000000000000000000000000000000000000000000000101
3.0000000000000002.toString(2) // 11

解答这些问题，就必须弄清楚进制转换和IEEE 754规范。

先了解一下进制转换，方便后面验证。

进制转换

十进制转换二进制

整数：采用 除2取余，逆序排列法 。具体做法是：用2整除十进制整数，可以得到一个商和余数；再用2去除商，又会得到一个商和余数，如此进行 ，直到商为小于1时为止，然后把先得到的余数作为二进制数的低位有效位，后得到的余数作为二进制数的高位有效位，依次排列起来。
小数：采用乘2取整，顺序排列法 。具体做法是：用2乘十进制小数，可以得到积，将积的整数部分取出，再用2乘余下的小数部分，又得到一个积，再将积的整数部分取出，如此进行，直到积中的小数部分为零，此时0或1为二进制的最后一位。或者达到所要求的精度为止。

我们使用 9.375 来分析

先看整数部分： 9 ，按照规则： 除2取余，逆序排列法

****结果为：1001

我们再来看小数部分：0.375 ，按照规则：乘2取整，顺序排列法

结果为：011

结合起来 9.375= 整数2 + 小数2 = 1001 + .011 = 1001.011

验证：

javascript 复制代码

console.log((9.375).toString(2))  // 1001.011
console.log(Number.prototype.toString.call(9.375, 2) )  // 1001.011
console.log(Number.prototype.toString.call( Number(9.375), 2))  // 1001.011

二进制转十进制

这个就交给读者自己查阅了。

IEEE 754

存储格式

JavaScript 采用 IEEE 754 标准来存储浮点数，以64位为例，64位双精度格式，数值精度最多可以达到 53 个二进制位。

为什么是 53 个，之后会有解答。

图片源于维基 Double-precision floating-point format

组成	位数	位置	说明
sign	1bit	63	符号位，0表示正，1表示负
exponent	11bit	52-62	指数部分
fraction	52bit	0-51	小数部分

规格化

浮点数，可以类似科学计数法一样，把数字表达为下面的格式。

(- 1) ^ S (1.M)2 ^ (E - 1023)

格式化换张图，更加好理解，大致分为三段，分别S, E, M三****部分。

名称	长度	比特位置	备注
符号位S	1bit	(b63)	1 表示负数，0表示正数
指数位E	11bit	(b62-b52)	实际指数 + 1023偏移量取值范围：1-2046
尾数部分M	52bit	(b51-b0)

这样做其中的一个好处是，1.M的M是52位，而1作为了一个隐藏位，实际上就是有53位来表达值。

指数位

11位的指数部分可存储00000000000 ~ 11111111111（十进制 0 ~ 2047），取值可分为3种情况：

指数值为11111111111（2047），这是特殊值
11位指数不为00000000000和11111111111，即在00000000001 ~ 11111111110（1 ~ 2046）范围，这被称为规格化。
指数值为00000000000（0），这被称为非规格化

详情可参见 IEEE 754 2008的 3.4 Binary interchange format encodings

至于为什么偏移码是1023，是因为指数部分有11位，表示范围0-2047(0b00000000000-0b11111111111)，也就是2048个值。但是指数有正负之分，所以就是-1024 到 +1024 。但是我们忘了中间还有个0，要占一个数值，所以只能表示-1024 到 +1023 。

一种做法是把高位变成1，表示负数，高位为0是正数。这样 0-1023(0b00000000000 - 0b01111111111) 表示正数，1024-2047(0b10000000000 - 0b11111111111) 表示负数(-1024 - -1)。不方便计算和比较。

另外一种，把所有的数加上1024 ，这样就全部变为正数了，也就是0-1024 表示负数，1025-2047 表示正数。那应该是1024 啊，不应该是1023，是因为特殊用处，0 和 2047 这两个值用来表示特殊数值，少了两个数，就用1023做偏移了。

接下来就先看看 2047 和 0 这两个特殊值。

特殊值

指数位全部为1，11111111111（十进制2047）

52位尾数部分全为0时，
- 若符号位是0，则表示+Infinity(正无穷)，
- 若符号位是1，则表示-Infinity(负无穷)
52位尾数部分不全为0时，表示NaN(Not a Number）
可以借用 IEEE 754 浮点数 - 在线工具去查看, 比如 +Infinity
1. 符号位 0
2. 指数位全为 1
3. 小数部分全为 0

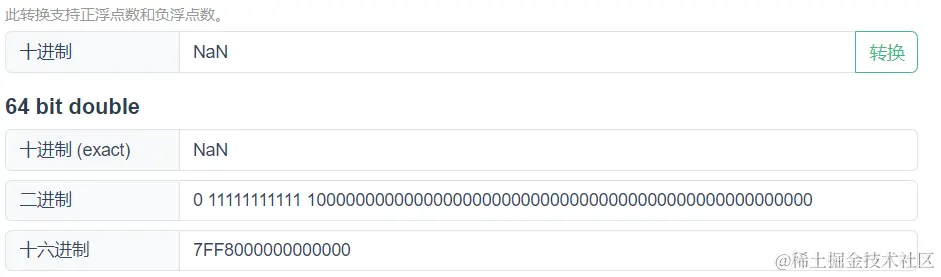
非规格化

指数部分全部为0，公式如下：

(- 1) ^ S (0.M)2 ^ (E-1022) (E=0)

当M部分全部为0的时候, 指数位已经不重要了，表示为0: s为0，表示+0， s为1 表示-0。

javascript 复制代码

(-1) ** 1  * 0 * 2 ** (-1022)  // -0
(-1) ** 0  * 0 * 2 ** (-1022)  //  0

非规格化的意义是什么呢？就是提供一种表示值0和接近0的方式。以规格化的方式，你是表示不出来0的。

小结

规格化数

表示最常见的数值, 比如0.567，123, 99999.999等等

特殊值（特殊的规格化数值）

指数位全为1，值2047

用于表示 +Infinity,-Infinit 和 NaN

非规格化数

指数位全为0，值0

表示0, 以及非常靠近0的数, 比如 5e-324, 这个后面浮点数表示范围会有解答.

计算 S，E，M

一起看个例子：

以十进制 30.0625 为例，为正数，
S位1 表示负数，0表示正数，本例为正数，故 S = 0
转为二进制

javascript 复制代码

30.0625.toString(2)  =>  11110.0001

规格化

十进制 100.01 可以表示为 1.0001 * 10^2, 二进制同理。

二进制可以转为 (1.xxxxxx) * 2 ^E 格式，其中 xxxxxx 为 M位置，E为指数位，不过这里需要加上偏移量。

javascript 复制代码

11110.0001 => 1.11100001 * 2 ^4

指数位为4，加上偏移量 1023，等于 1023 + 4 = 1027，二进制为 10000000011

M位为 11100001

最终存储

名称	长度	比特位置	值
符号位S	1bit	(b63)	0
指数位E	11bit	(b62-b52)	10000000011
尾数部分M	52bit	(b51-b0)	1110000100000000000000000000000000000000000000000000

可以使用IEEE 754 浮点数 - 在线工具去验证结果。

根据 S M E 求值

求值公式：V = (- 1) ^ S (1.M)2 ^ (E - 1023), 把上面的S ，E ，M数据代入

(-1)^0 = 1
1.M = 1.1110000100000000000000000000000000000000000000000000
E-1023 = 4
代入
1 * 1.1110000100000000000000000000000000000000000000000000 * 2^4
2^4等于向左移动4位
11110.000100000000000000000000000000000000000000000000
去掉多余的位数
11110.0001
0b11110 + 0b0001/(2**4)
30 + 0.0625
30.0625

浮点数表示范围

浮点数规格化最大正值

公式：V= (- 1) ^ S (1.M)2 ^ (E - 1023)

名称	长度	比特位置	备注
符号位S	1bit	(b63)	1 表示负数，0表示正数
指数位E	11bit	(b62-b52)	指数 + 1023偏移量
尾数部分M	52bit	(b51-b0)

求最大值, S=0为 正数， M, E位取最大值即可：

S为0，表示正数
E取值范围1-2046, 取值2046，减掉偏移量 2046 - 1023 = 1023
M值，52位全部设置为1

javascript 复制代码

//1位    11位指数位  52位M位置
0       11111111110 1111111111111111111111111111111111111111111111111111

1 * 1.1111111111111111111111111111111111111111111111111111 * 2**1023

= 1.1111111111111111111111111111111111111111111111111111 * 2** (52 + 971)

= 0b11111111111111111111111111111111111111111111111111111 * 2** 971

= 1.7976931348623157e+308

javascript 复制代码

 Number.MAX_VALUE   //  1.7976931348623157e+308
 Number.MAX_VALUE === 0b11111111111111111111111111111111111111111111111111111 * 2** 971 // true

浮点数规格化最小负值

这里就得正确理解最小负值和最大负值，如下的四个值， -100 是小于 -1的， -100 是最小负值，而 -1 是最大负值。

javascript 复制代码

最小负值        最大负值     最小正值     最大正值
  -100           -1           1           100

求最小值, S=1为 正数， M, E位取最大值即可：

S为1，表示负数
E取值范围1-2046, 取值2046，减掉偏移量 2046 - 1023 = 1023
M值，52位全部设置为1

仅仅是符号位不同，规格化最小负值就是最大正值对应的负值。

-1.7976931348623157e+308

浮点数规格化最小正值

公式：V= (- 1) ^ S (1.M)2 ^ (E - 1023)

S为0，表示正数
E取值范围1-2046, 取最小值1，减掉偏移量 1 - 1023 = -1022
M值，52位全部设置为0，存储如下

javascript 复制代码

//1位    11位指数位  52位M位置
1       00000000001 0000000000000000000000000000000000000000000000000000

带入公式

1 * 1.0000000000000000000000000000000000000000000000000000 * 2**(-1022)

= 0b1 * 2**(-1022)

= 2.2250738585072014e-308

浮点数规格化最大负值

就是上面的最小正值取负值。

-2.2250738585072014e-308

浮点数非规格化最大正值

公式： (- 1) ^ S (0.M)2 ^ (E-1022) (E=0)

S取0，表示正数，
M的52位全部取1，E取值可以得到最大值。

1 * 0.1111111111111111111111111111111111111111111111111111 * 2 ** (-1022)

1 * 0.1111111111111111111111111111111111111111111111111111 * 2 ** (52-1022-52)

0b1111111111111111111111111111111111111111111111111111 * 2 ** (-1074)

2.225073858507201e-308

浮点数非规格化最小负值

就是非规格化的最大值取负值。

-2.225073858507201e-308

浮点数非规格化最小正值

公式： (- 1) ^ S (0.M)2 ^ (E-1022) (E=0)

S取0，表示正数， M第52位取1，可以得到最小值。

1 * 0.0000000000000000000000000000000000000000000000000001 * 2 ** (-1022)

1 * 0.0000000000000000000000000000000000000000000000000001 * 2 ** (52-1022-52)

1 * 0.0000000000000000000000000000000000000000000000000001 * 2 ** 52 * 2 ** (-1074)

1 * 1 * 2 ** (-1074)

1 * 2 ** (-1074)

javascript 复制代码

1 * 2 ** (-1074)     /   / 5e-324
1 * 2 ** (-1074)  === Number.MIN_VALUE  // true

浮点数非规格化最大负值

就是对上面的最小正值取负值。

-5e-324

取值小结

	最小负值	最大负值	最小正值	最大正值
规格化	-1.7976931348623157e+308	-2.2250738585072014e-308	2.2250738585072014e-308	1.7976931348623157e+308
非规格化	-5e-324	2.225073858507201e-308	5e-324	2.225073858507201e-308

这时候再一起来看，Number.MIN_VALUE和 Number.MAX_VALUE，先不说话，只看输出

javascript 复制代码

Number.MIN_VALUE     // 5e-324
Number.MAX_VALUE     // 1.7976931348623157e+308

可以得到所谓的MIN_VALUE和 MAX_VALUE都是正值，表示其能表示的最小正数和最大正数。
Number.MAX_VALUE是规格化的最大正值
Number.MIN_VALUE是非规格化的最小正值
超过 Number.MAX_VALUE为 Infinity, 小于 -Number.MAX_VALUE为 -Infinity。

javascript 复制代码

1.7976931348623157e+308 + 1e320  // Infinity
-1.7976931348623157e+308 - 1e320 // -Infinity

Number.MIN_VALUE和 -Number.MIN_VALUE之间的显示为0

整数

Number.MAX_SAFE_INTEGER

ES6 有 Number.MAX_SAFE_INTEGER和 Number.MIN_SAFE_INTEGER两个常量分别表示这个范围的上下限。

javascriptjavascript 复制代码

Number.MAX_SAFE_INTEGER   // 9007199254740991
Number.MIN_SAFE_INTEGER   // -9007199254740991

其值分别对应着 2**53 - 1 和 -(2**53-1)

javascript 复制代码

Number.MAX_SAFE_INTEGER === 2**53 - 1
Number.MIN_SAFE_INTEGER === -(2**53-1)

这个又从何而来，一起回到规格化公式和图：

(- 1) ^ S (1.M)2 ^ (E - 1023)

M部分有52位小数，如果 0.01想要变为整数至少乘10**2，对于二进制是一样的，指数部分需要保留52位，最多52位才是安全整数。为啥呢，因为如果M最多能保留52位，多余52位就会出现精度问题，其限制了指数的大小。

所以下列条件表示最大正整数

E-1023 = 52的时候，E = 1075 最大指数
M部分全为1

1 * 1.1111111111111111111111111111111111111111111111111111 * 2 ** 52

11111111111111111111111111111111111111111111111111111 （53位）

2**53-1

javascriptjavascriptjavascript 复制代码

0b11111111111111111111111111111111111111111111111111111  // 9007199254740991
2**53-1  // 9007199254740991

S符号取1，即得到最大负整数： -9007199254740991

注意事项

大于 Number.MAX_SAFE_INTEGER或者小于 Number.MIN_SAFE_INTEGER的数，因为精度问题，可能发生惊喜。

javascriptjavascript 复制代码

9007199254740999    // 9007199254741000
-9007199254740994   // -9007199254741000

那怎么确保某个整数的运算是安全的的呢？

javascript 复制代码

9007199254740991 + 9
9007199254740991 * 2

做法就是检查每个操作数，以及操作的结果是不是安全的整数

javascript 复制代码

 Number.isSafeInteger(9007199254740991)       // true
 Number.isSafeInteger(9)                      // true  
 Number.isSafeInteger(9007199254740991 + 9)   // false

进行简单的包装

javascript 复制代码

function isSafeInt(intNum){
  return  Number.isSafeInteger(intNum);
}

function safeIntegerOperation(...args){
    const isSafe = args.every(isSafeInt);
    if(isSafe){
      return args.pop();
    }
    throw new Error('不是安全的操作');
}

safeIntegerOperation(9007199254740991,9, 9007199254740991+9)  // VM2704:10 Uncaught Error: 不是安全的操作
safeIntegerOperation(3,9, 3 + 9)  // 12

重回Number.isInteger

javascript 复制代码

Number.isInteger(3.000000000000002)      // 14个0 false
Number.isInteger(3.0000000000000002)     // 15个0 true

3.000000000000002 (14个0)

为整数， S = 0
转为二进制

javascript 复制代码

11.00000000000000000000000000000000000000000000000010 0100...

// 尾数部分，可以参考
3.toString(2) => 11 
0.000000000000002.toString(2) =>
00.00000000000000000000000000000000000000000000000010 0100 0000011101011111001111011100111010101100001011

3 . 规格化，转为 1.M 格式

javascript 复制代码

1.100000000000000000000000000000000000000000000000010 0100...

E = 1023 + 1 = 1024

M = 00000000000000000000000000000000000000000000000010 0100...

保留52位

javascript 复制代码

// 51位                                            // 52位以及以后                                            	
100000000000000000000000000000000000000000000000010 0100...

// 51                                               52  53 54 55                                    	
100000000000000000000000000000000000000000000000010  0  1  0  0...

// 保留52位, 四舍五入， 53位为1，进位，52位变为1                             
// 51                                               52  53 54 55                                    	
100000000000000000000000000000000000000000000000010  0  1  0  0...
// 51                                               52  53 54 55                                    	
100000000000000000000000000000000000000000000000010  1

符号位S	0 （十进制0）
指数位E	10000000000 （十进制 1024 = 1 + 1023）
尾数部分M	100000000000000000000000000000000000000000000000010 1

采用toString验证一下，值还并未失真。

javascript 复制代码

3.000000000000002.toString(2)
11.000000000000000000000000000000000000000000000000101

如果小数部分的0从14位变为15位呢？

javascript 复制代码

Number.isInteger(3.000000000000002)      // 14个0 false
Number.isInteger(3.0000000000000002)     // 15个0 true

3.0000000000000002 （15个0）

javascript 复制代码

11.00000000000000000000000000000000000000000000000000 00111101
// 规格化
1.100000000000000000000000000000000000000000000000000 00111101.... * 2 ** 1

// M部分保留 52位, 53位为0， 丢弃
// 51                                               52 53 54
100000000000000000000000000000000000000000000000000  0  0  1  11101....

// 最终M的值
100000000000000000000000000000000000000000000000000  0

// 上面的小数部分的值，来源下面
0.0000000000000002.toString(2)
00.00000000000000000000000000000000000000000000000000 00111001 101001010110010100101111101100010001001101111

符号位S	0 （十进制0）
指数位E	10000000000 （十进制1024 = 1 + 1023）
尾数部分M	100000000000000000000000000000000000000000000000000 0

采用toString验证一下，哦豁，精度已经丢失了。

javascript 复制代码

3.0000000000000002.toString(2) // 11
11.000000000000000000000000000000000000000000000000000  === 11  // true

以IEEE标准存储数字的时候，M位仅仅保留52位，如果多余52位，会四舍五入，导致精度出现问题。所以导致Number.isInterger判断不准。

思考 0.1 + 0.2

javascript 复制代码

0.1 + 0.2 !== 0.3  // true
0.1 + 0.2  // 0.30000000000000004

这个和IEEE 754 肯定是脱不了关系的，不过浮点数加减有一些既有的步骤：

对阶
位数运算
结果规格化
舍入处理
溢出检查

本文就不深入讲解了，明白IEEE 754 的存储规则，都不难理解。

在日常开发过程中，出现小数很正常，比如钱，增长率等，如果不做特殊处理，出现一大长串数字，这就很尴尬。

Number.prototype.toFixed

数据吗，毕竟是要渲染到界面上，渲染前调用toFixed，转为字符串，可以保留固定位数。

javascript 复制代码

(0.1+0.2).toFixed(2) // 0.30

乘以10n, 再除以10n

javascript 复制代码

(0.1 * 100 +0.2 * 100)/100  // 0.3

借助 Number.EPSILON

Number.EPSILON 是JS能表示的最小精度，二进制的52位，十进制的 2 ** -52。

javascript 复制代码

Number.EPSILON === 2 ** -51   // false
Number.EPSILON === 2 ** -52   // true
Number.EPSILON === 2 ** -53   // false

自定义一个可自定义误差的等于方法，当然肯定不建议比较到2进制的50多位，这时候本来就存在四舍五入的情况，比如定义为20位，日常肯定就满足需求了。

javascript 复制代码

// 比较相等，默认比较到52位，figures以52位为基础增减
function equal (num1, num2, figures = 52) {
  return Math.abs(num1 - num2) < Number.EPSILON *(2 ** (52 - figures));
};

// 比较到54位
equal(0.1 + 0.2 , 0.3, 54);  // false
// 比较到52位
equal(0.1 + 0.2 , 0.3, 52);      // true
// 精确到二进制的20位
equal(0.1 + 0.2 , 0.3, 20);   // true

再思考

javascript 复制代码

Number.EPSILON + Number.MAX_VALUE === Number.MAX_VALUE

引用

Double-precision floating-point format
IEEE 754 | 维基
 IEEE 754 2008
IEEE 754 浮点数 - 在线工具
 JavaScript中奇特的~运算符

ECMAScript 杂谈：再谈数值

前言

准备

字符串转为数值

转为浮点数 parseFloat

转为整数 parseInt

使用一元 + 转为数值

使用位移 转为数值

0 和 -0

区别 0 和 -0

Smi 和 HEAP_NUMBER_TYPE

NaN

特点

精准识别

数组includes注意

Number.isInteger

进制转换

十进制转换二进制

二进制转十进制

IEEE 754

存储格式

规格化

特殊值

非规格化

小结

计算 S，E，M

根据 S M E 求值

浮点数表示范围

浮点数规格化最大正值

浮点数规格化最小负值

浮点数规格化最小正值

浮点数规格化最大负值

浮点数非规格化最大正值

浮点数非规格化最小负值

浮点数非规格化最小正值

浮点数非规格化最大负值

取值小结

整数

Number.MAX_SAFE_INTEGER

注意事项

重回Number.isInteger

3.000000000000002 (14个0)

3.0000000000000002 （15个0）

思考 0.1 + 0.2

再思考

引用

转为浮点数 `parseFloat`

转为整数 `parseInt`

使用位移转为数值