众所周知,数组可以以 \(O(1)\) 的复杂度查询、修改元素,但删除和插入元素的复杂度是 \(O(n)\) 的;链表恰好相反,插入、删除元素的复杂度为 \(O(1)\),但查询为 \(O(n)\)。
有没有能以较优复杂度完成插入、删除、查询、修改操作的线性数据结构?
本篇介绍的块状链表就可以。
顾名思义,块状链表运用分块的思想,将数组与链表结合起来。这里引用一张经典的图来展示它大概的样子:
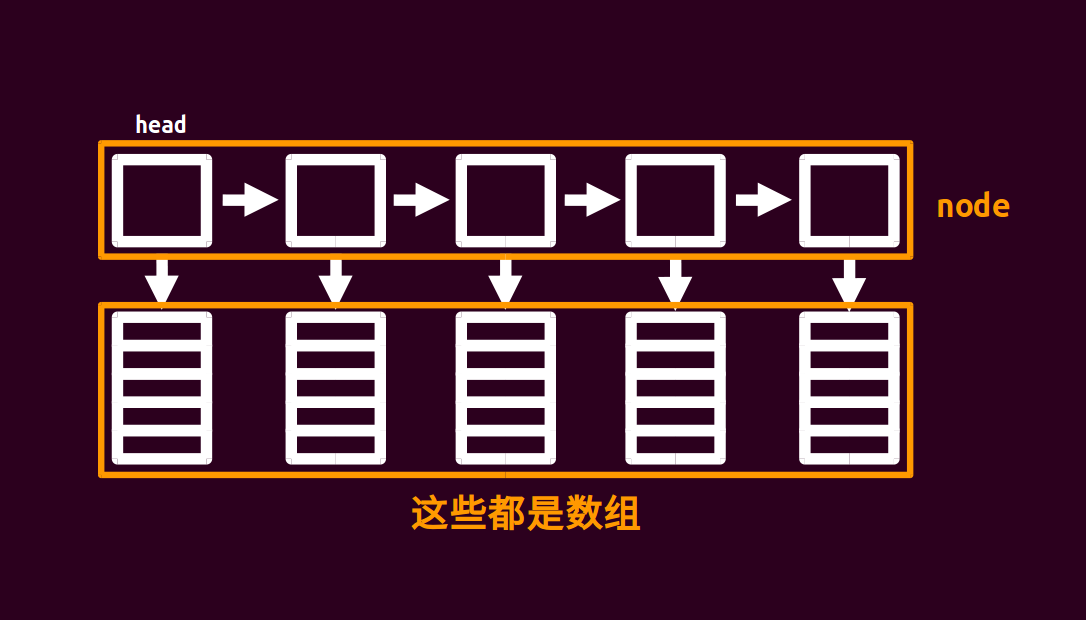
可以看出块状链表就是以数组为节点(块)的链表。
例一
我们借P4008 [NOI2003] 文本编辑器这道题来理解块状链表的各个操作。
维护一个字符串,支持在指定位置插入字符串、删除字符串、查询指定长度的连续字串。
内存分配
与正常的链表一样,块状链表中会出现很多新建、删除节点的操作,必须让被删除节点的位置能被新节点再次占用,否则会产生很多空节点,从而使内存巨大。为此我们使用作为内存池的栈 \(pool[]\)。
void init()
{
for(int i=1;i<=mxnum;i++)//初始化内存池
pool[i]=i;
sz[0]=0;
nxt[0]=-1;//标记链表的结尾
}
int new_block()
{
return pool[++num];//取出栈顶空节点
}
void del_block(int x)
{
pool[num--]=x;//将被删除的节点压入栈顶
}合并
为了保证复杂度,需要同时限制块的总数与最大块长。一个很好的方法是,对于相邻的块,如果他们的长度和不超过最大块长,就将他们合并。
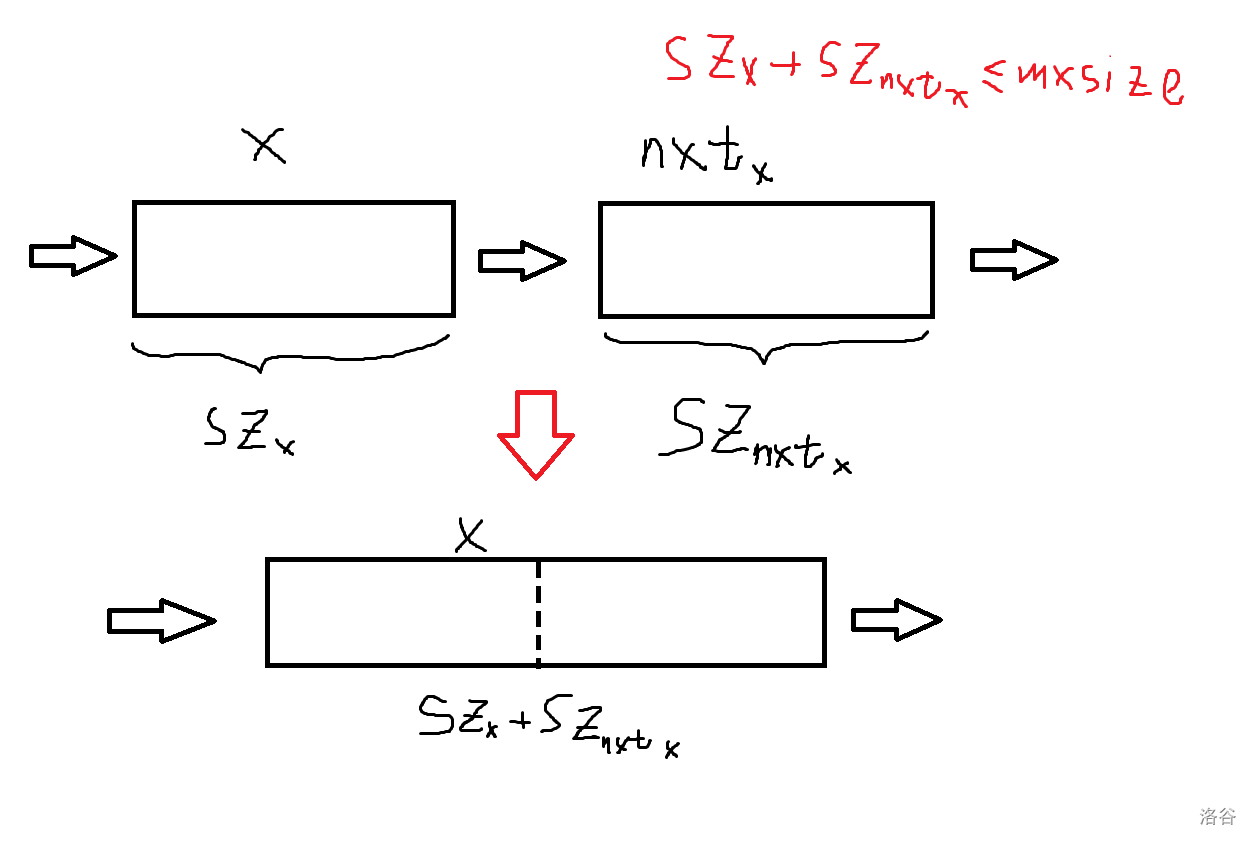
void merge(int x,int y)
{
cpy(dt[x]+sz[x],dt[y],sz[y]);//手写的复制函数,与memcpy功能相同
nxt[x]=nxt[y];
sz[x]+=sz[y];
del_block(y);//合并后,多出来的块要删掉
}
void maintain()//遍历整个链表,合并所有可以合并的相邻块
{
for(int x=0,y=nxt[0];x!=-1;x=nxt[x],y=nxt[x])
while(y!=-1 && sz[x]+sz[y]<=mxsize)
{
merge(x,y);
y=nxt[x];
}
}分裂
在插入或删除元素时,需要将待操作位置单独分成块,再进行类似链表的插入、删除操作。
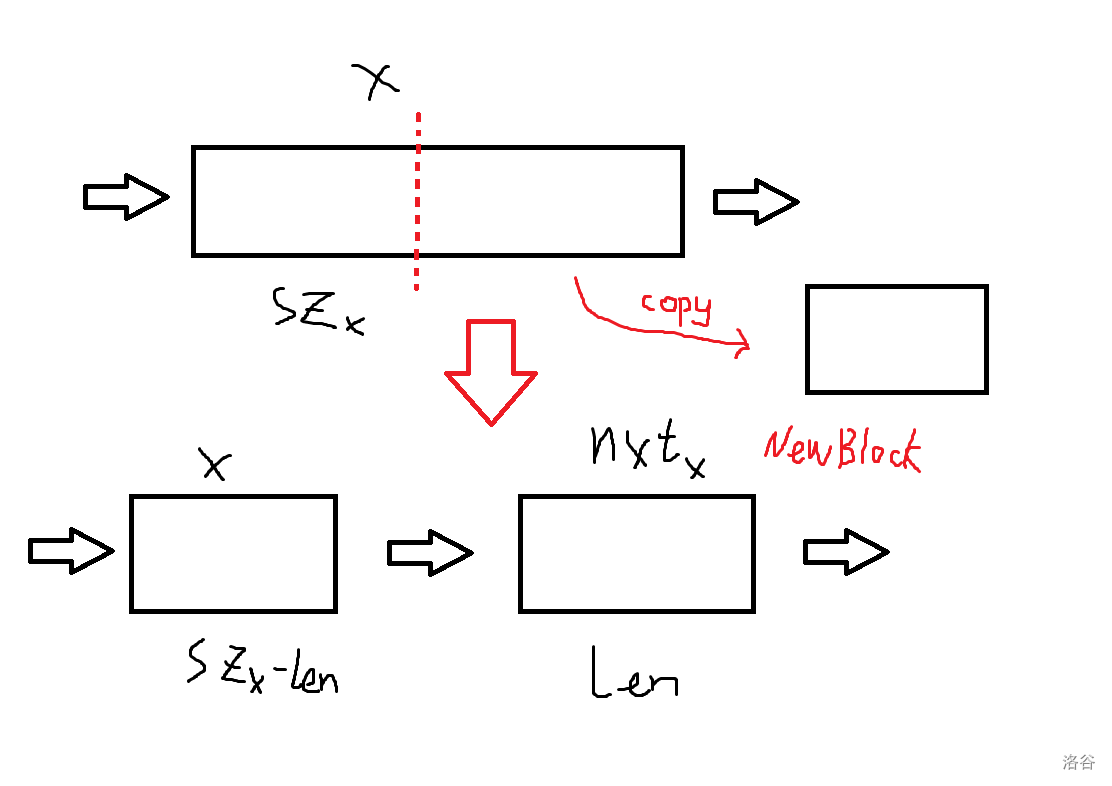
void update(int x,int y,int len,char *s)
{
nxt[y]=nxt[x];
nxt[x]=y;
sz[y]=len;
cpy(dt[y],s,len);
}
void split(int x,int pos)
{
if(x==-1 || pos==sz[x])
return;
int y=new_block();
update(x,y,sz[x]-pos,dt[x]+pos);//新建块
sz[x]=pos;//记得更新原块长
}具体操作
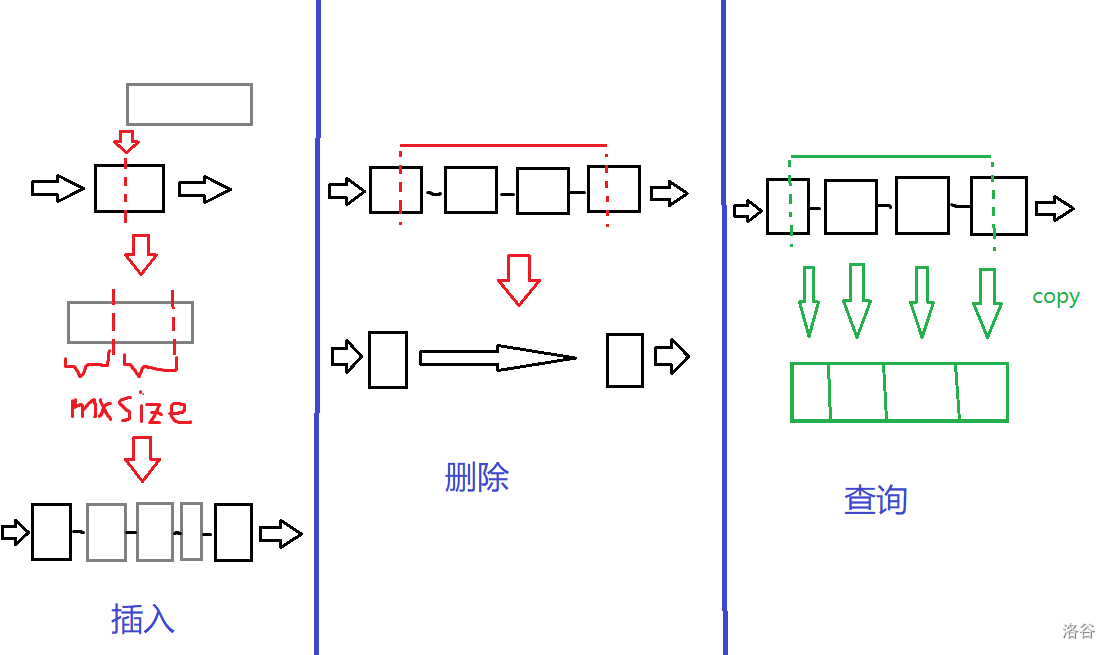
-
插入:将插入位置的块分裂,把待插入字符串分成长度不超过 \(mxsize\) 的块,依次插入。
-
删除:将要删除的左右端点的块分裂,删去中间所有块。
-
查询:将会被查到的所有块复制到答案字符串上。
int get_pos(int &pos)//将输入的位置转换成块上的位置
{
int x=0;
while(x!=-1 && pos>sz[x])
{
pos-=sz[x];
x=nxt[x];
}
return x;
}void insert(int pos,int len)
{
int x=get_pos(pos),y,sum=0;
split(x,pos);while(sum+mxsize<=len) { y=new_block(); update(x,y,mxsize,s+sum); sum+=mxsize; x=y; } if(len>sum)//如果切完后还有剩余,尾部自成一块 { y=new_block(); update(x,y,len-sum,s+sum); } maintain();//插入的左、右端点处可能可以合并,后面删除操作的maintain()同理}
void erase(int pos,int len)
{
int x=get_pos(pos),y;
split(x,pos);
y=nxt[x];while(y!=-1 && len>0) { if(sz[y]>len) split(y,len); len-=sz[y]; del_block(y); y=nxt[y]; } nxt[x]=y;//记得指向下一块 maintain();}
void query(int pos,int len)
{
int x=get_pos(pos),sum=sz[x]-pos;
if(len<sum)
sum=len;cpy(s,dt[x]+pos,sum); x=nxt[x]; while(x!=-1 && sum+sz[x]<=len) { cpy(s+sum,dt[x],sz[x]); sum+=sz[x]; x=nxt[x]; } if(x!=-1 && len>sum) cpy(s+sum,dt[x],len-sum); s[len]=0;//标记串的结尾 printf("%s\n",s);}
总体代码
#include <bits/stdc++.h>
using namespace std;
const int N=1024*1024+5;
const int mxsize=3000,mxnum=N*2/mxsize+5;//要开到N的两倍
int q;
int num,nxt[mxnum],sz[mxnum],pool[mxnum];
char dt[mxnum][mxsize],s[N];
void cpy(char *a,char *b,int len)
{
for(int i=0;i<len;i++)
*(a+i)=*(b+i);
}
void gets(int len)
{
for(int i=0;i<len;i++)
{
s[i]=0;
while(s[i]<32 || s[i]>126)
s[i]=getchar();
}
}
//省略
int main( void )
{
scanf("%d",&q);
init();
int pos=0;
while(q--)
{
char rd[10];
scanf("%s",rd);
if(rd[0]=='M')
scanf("%d",&pos);
else if(rd[0]=='I')
{
int len;
scanf("%d",&len);
gets(len);
insert(pos,len);
}
else if(rd[0]=='D')
{
int len;
scanf("%d",&len);
erase(pos,len);
}
else if(rd[0]=='G')
{
int len;
scanf("%d",&len);
query(pos,len);
}
else if(rd[0]=='P')
pos--;
else if(rd[0]=='N')
pos++;
}
return 0;
}例二
给定一个长度为 \(n\) 的序列 \(a\),初始 \(a_i=i\),执行多次区间翻转操作,求操作后序列。
将需要翻转的区间中的所有块顺序翻转,并给每一块打上翻转标记,在合并、分裂时检查标记。
void rev(int x)
{
if(tag[x])
reverse(a[x],a[x]+sz[x]);
tag[x]=0;//翻转后取消标记
}
void rotate(int pos,int len)
{
int x=get_pos(pos);
split(x,pos);
int y=nxt[x];
top=0;
while(len>0)
{
if(sz[y]>len)
split(y,len);
len-=sz[y];
sta[++top]=y;
tag[y]^=1;//注意这里不能直接=1
y=nxt[y];
}
sta[++top]=x;
sta[0]=y;
for(;top>=1;top--)
nxt[sta[top]]=sta[top-1];//反着连接块
maintain();
}例三
给定一个 \(1\)~\(n\) 的排列,操作为将某个数放到最前面、放到最后面或向前、后移动一步,询问 \(s\) 位置的数或数 \(s\) 的位置。
这三种操作都可以视为从排列中删除一个数,再插入一个数。
这道题中比较麻烦的一点是,移动数的操作给定的都是数的值,因此可以给每一个块开一个桶 \(book[]\) 以记录其中是否包含某个数,进行移动操作之前先查询位置。
#include <bits/stdc++.h>
using namespace std;
const int N=405;
int n,m,k;
int a[N][N],sz[N],pool[N],nxt[N],book[N][80005];
void init()
{
for(int i=1;i<=N-5;i++)
pool[i]=i;
nxt[0]=-1;
}
int new_block()
{
return pool[++k];
}
void del_block(int x)
{
for(int i=0;i<sz[x];i++)
book[x][a[x][i]]=0;//记得清空book
pool[k--]=x;
}
void cpy(int *a,int *b,int len)
{
for(int i=0;i<len;i++)
*(a+i)=*(b+i);
}
void merge(int x,int y)
{
cpy(a[x]+sz[x],a[y],sz[y]);
nxt[x]=nxt[y];
sz[x]+=sz[y];
for(int i=0;i<sz[y];i++)
book[x][a[y][i]]=1;
del_block(y);
}
void maintain()
{
for(int x=0,y=nxt[0];x!=-1;x=nxt[x],y=nxt[x])
while(y!=-1 && sz[x]+sz[y]<=400)
{
merge(x,y);
y=nxt[x];
}
}
void update(int x,int y,int len,int *c)
{
nxt[y]=nxt[x];
nxt[x]=y;
sz[y]=len;
cpy(a[y],c,len);
for(int i=0;i<sz[y];i++)
book[y][a[y][i]]=1;
}
void split(int x,int pos)
{
if(x==-1 || pos==sz[x])
return;
int y=new_block();
update(x,y,sz[x]-pos,a[x]+pos);
sz[x]=pos;
for(int i=0;i<sz[y];i++)
book[x][a[y][i]]=0;
}
int get_pos(int &pos)
{
int x=0;
while(x!=-1 && pos>sz[x])
{
pos-=sz[x];
x=nxt[x];
}
return x;
}
void insert(int pos,int num)
{
int x=get_pos(pos);
split(x,pos);
int y=new_block();
update(x,y,1,&num);
maintain();
}
void remove(int pos)
{
int x=get_pos(pos);
split(x,pos);
int y=nxt[x];
split(y,1);
nxt[x]=nxt[y];
del_block(y);
maintain();
}
int query(int pos)
{
int x=get_pos(pos);
return a[x][pos-1];
}
int askk(int id)
{
int x=0,num=0;
while(!book[x][id])
{
num+=sz[x];
x=nxt[x];
}//跳到包含id的块
for(int i=0;i<sz[x];i++,num++)
if(a[x][i]==id)//找到id具体位置
return num;
}
void top(int id)
{
if(askk(id)!=0)//判断边界
{
remove(askk(id));
insert(0,id);
}
}
void bottom(int id)
{
if(askk(id)!=n-1)
{
remove(askk(id));
insert(n-1,id);
}
}
void step(int id,int t)
{
if(!t)
return;
int pos=askk(id);
if(t==1)
if(pos!=n-1)
{
remove(pos);
insert(pos+1,id);
}
if(t==-1)
if(pos!=0)
{
remove(pos);
insert(pos-1,id);
}
}
int main( void )
{
scanf("%d%d",&n,&m);
init();
for(int i=1;i<=n;i++)
{
int x;
scanf("%d",&x);
insert(i-1,x);
}
for(int i=1;i<=m;i++)
{
char c[10];
int s,t;
scanf("%s%d",c,&s);
if(c[0]=='T')
top(s);
else if(c[0]=='B')
bottom(s);
else if(c[0]=='I')
{
scanf("%d",&t);
step(s,t);
}
else if(c[0]=='A')
printf("%d\n",askk(s));
else if(c[0]=='Q')
printf("%d\n",query(s));
}
return 0;
}