为什么重写equals一定也要重写hashCode方法？

seven97_top2025-05-06 8:25

简要回答

这个是针对set和map这类使用hash值的对象来说的

  1. 只重写equals方法，不重写hashCode方法：

    • 有这样一个场景有两个Person对象，可是如果没有重写hashCode方法只重写了equals方法，equals方法认为如果两个对象的name相同则认为这两个对象相同。这对于equals判断对象相等是没问题的。

    • 对于set和map这类使用hash值的对象来说，由于没有重写hashCode方法，此时返回的hash值是不同的，因此不会去判断重写的equals方法，此时也就不会认为是相同的对象。

  2. 重写hashCode方法不重写equals方法

    • 不重写equals方法实际是调用Object方法中的equals方法，判断的是两个对象的堆内地址。而hashCode方法认为相等的两个对象在equals方法处并不相等。因此也不会认为是用一个对象

    • 因此重写equals方法时一定也要重写hashCode方法，重写hashCode方法时也应该重写equals方法。

总结：对于普通判断对象是否相等来说，只equals是可以完成需求的，但是如果使用set，map这种需要用到hash值的集合时，不重写hashCode方法，是无法满足需求的。尽管如此，也一般建议两者都要重写，几乎没有见过只重写一个的情况

详细介绍

==

"==" 是运算符

  1. 如果比较的对象是基本数据类型，则比较的是其存储的值是否相等；

  2. 如果比较的是引用数据类型，则比较的是所指向对象的地址值是否相等（是否是同一个对象）。

java 复制代码 
Person p1 = new Person("123");
Person p2 = new Person("123");
int a = 10;
int b = 10;
System.out.println(a == b);//true
System.out.println(p1 == p2); //显然不是同一个对象,false

equals

作用是 用来判断两个对象是否相等。通过判断两个对象的地址是否相等(即，是否是同一个对象)来区分它们是否相等。源码如下：

java 复制代码 
public boolean equals(Object obj) {
    return (this == obj);
}

equals 方法不能用于比较基本数据类型，如果没有对 equals 方法进行重写，则相当于"=="，比较的是引用类型的变量所指向的对象的地址值。

一般情况下，类会重写equals方法用来比较两个对象的内容是否相等。比如String类中的equals()是被重写了，比较的是对象的值。

hashcode

  1. hashcode特性体现主要在它的查找效率上，O(1)的复杂度，在Set和Map这种使用哈希表结构存储数据的集合中。hashCode方法的就大大体现了它的价值，主要用于在这些集合中确定对象在整个哈希表中存储的区域。

  2. 如果两个对象相同，则这两个对象的equals方法返回的值一定为true，两个对象的hashCode方法返回的值也一定相同。(equals相同，hashcode一定相同，因为重写的hashcode就是计算属性的hashcode值)

  3. 如果两个对象返回的HashCode的值相同，但不能够说明这两个对象的equals方法返回的值就一定为true，只能说明这两个对象在存储在哈希表中的同一个桶中。

只重写了equals方法，未重写hashCode方法

在Java中equals方法用于判断两个对象是否相等，而HashCode方法在Java中主要由于哈希算法中的寻域的功能（也就是寻找数据应该存储的区域的）。在类似于set和map集合的结构中，Java为了提高在集合中查询匹配元素的效率问题，引入了哈希算法，通过HashCode方法得到对象的hash码，再通过hash码推算出数据应该存储的位置。然后再进行equals操作进行匹配，减少了比较次数，提高了效率。

java 复制代码 
public class Person {
    String name;

    public Person(String name) {
        this.name = name;
    }

    @Override
    public boolean equals(Object o) {
        if (this == o) return true;
        if (o == null || getClass() != o.getClass()) return false;
        Person person = (Person) o;
        return Objects.equals(name, person.name);
    }

    public static void main(String[] args) {
        Person p1 = new Person("123");
        Person p2 = new Person("123");

        System.out.println(p1 == p2);//false
        System.out.println(p1.hashCode() == p2.hashCode());//false
        System.out.println(p1.equals(p2));//true

        Set<Person> set = new HashSet<>();
        set.add(p1);
        set.add(p2);
        System.out.println(set.size());//2
    }
}

  • 当只重写了equals方法，未重写hashCode方法时，equals方法判断两个对象是否相等时，返回的是true(第三个输出)，这是因为我们重写equals方法时，是对属性的比较；但判断两个对象的hashCode值是否相等时，返回的是false(第二个输出)，在没有重写hashCode方法的情况下，调用的是Object的hashCode方法，返回的是本对象的hashCode值，两个对象不一样，因此hashCode值不一样。

  • 在set和map中，首先判断两个对象的hashCode方法返回的值是否相等，如果相等然后再判断两个对象的equals方法，如果hashCode方法返回的值不相等，则直接会认为两个对象不相等，不进行equals方法的判断。因此在set添加对象时，因为hashCode值已经不一致，判断出p1和p2是两个对象，都会添加进set集合中，因此返回集合中数据个数为 2 (第四个输出)

重写hashCode方法：重写hashcode方法时，一般也是对属性值进行hash

java 复制代码 
@Override
public int hashCode() {
    return Objects.hash(name);
}

重写了hashCode后，其是对属性值的hash，p1和p2的属性值一致，因此p1.hashCode() == p2.hashCode()为true，再进行equals方法的判断也为true，认为是一个对象，因此set集合中只有一个对象数据。

为什么重写hashCode一定也要重写equals方法？

如果两个对象的hashCode相同，它们是并不一定相同的，因为equals方法不相等而hashCode方法返回的值却有可能相同的，比如两个不同的对象hash到同一个桶中

hashCode方法实际上是通过一种算法得到一个对象的hash码，这个hash码是用来确定该对象在哈希表中具体的存储区域的。返回的hash码是int类型的所以它的数值范围为 [-2147483648 - +2147483647] 之间的，而超过这个范围，实际会产生溢出，溢出之后的值实际在计算机中存的也是这个范围的。比如最大值 2147483647 + 1 之后并不是在计算机中不存储了，它实际在计算机中存储的是-2147483648。在java中hash码也是通过特定算法得到的，所以很难说在这个范围内情况下不会不产生相同的hash码的。也就是说常说的哈希碰撞，因此不同对象可能有相同的hashCode的返回值。

因此equals方法返回结果不相等，而hashCode方法返回的值却有可能相同！

为什么重写equals一定也要重写hashCode方法？

这个是针对set和map这类使用hash值的对象来说的

  1. 只重写equals方法，不重写hashCode方法：

    • 有这样一个场景有两个Person对象，可是如果没有重写hashCode方法只重写了equals方法，equals方法认为如果两个对象的name相同则认为这两个对象相同。这对于equals判断对象相等是没问题的。

    • 对于set和map这类使用hash值的对象来说，由于没有重写hashCode方法，此时返回的hash值是不同的，因此不会去判断重写的equals方法，此时也就不会认为是相同的对象。

  2. 重写hashCode方法不重写equals方法

    • 不重写equals方法实际是调用Object方法中的equals方法，判断的是两个对象的堆内地址。而hashCode方法认为相等的两个对象在equals方法处并不相等。因此也不会认为是用一个对象

    • 因此重写equals方法时一定也要重写hashCode方法，重写hashCode方法时也应该重写equals方法。

总结：对于普通判断对象是否相等来说，只equals是可以完成需求的，但是如果使用set，map这种需要用到hash值的集合时，不重写hashCode方法，是无法满足需求的。尽管如此，也一般建议两者都要重写，几乎没有见过只重写一个的情况

解决哈希冲突的三种方法

拉链法

HashMap，HashSet其实都是采用的拉链法来解决哈希冲突的，就是在每个位桶实现的时候，采用链表的数据结构来去存取发生哈希冲突的输入域的关键字（也就是被哈希函数映射到同一个位桶上的关键字）

但是如果hash 冲突⽐较严重，链表会⽐较⻓，查询的时候，需要遍历后⾯的链表，因此JDK 优化了⼀版，链表的⻓度超过阈值的时候，会变成红⿊树，红⿊树有⼀定的规则去平衡⼦树，避免退化成为链表，影响查询效率。

但是你肯定会想到，如果数组太⼩了，放了⽐较多数据了，怎么办？再放冲突的概率会越来越⾼，其实这个时候会触发⼀个扩容机制，将数组扩容成为 2 倍⼤⼩，重新hash 以前的数据，哈希到不同的数组中。

hash 表的优点是查找速度快，但是如果不断触发重新 hash , 响应速度也会变慢。同时，如果希望范围查询， hash 表不是好的选择。

拉链法的装载因子为n/m（n为输入域的关键字个数，m为位桶的数目）

开放地址法

所谓开放地址法就是发生冲突时在散列表（也就是数组里）里去寻找合适的位置存取对应的元素，就是所有输入的元素全部存放在哈希表里。也就是说，位桶的实现是不需要任何的链表来实现的，换句话说，也就是这个哈希表的装载因子不会超过1。

它的实现是在插入一个元素的时候，先通过哈希函数进行判断，若是发生哈希冲突，就以当前地址为基准，根据再寻址的方法（探查序列），去寻找下一个地址，若发生冲突再去寻找，直至找到一个为空的地址为止。

探查序列的方法:

  • 线性探查

  • 平方探测

  • 伪随机探测

线性探查

di =1，2，3，...，m-1；这种方法的特点是：冲突发生时，顺序查看表中下一单元，直到找出一个空单元或查遍全表。

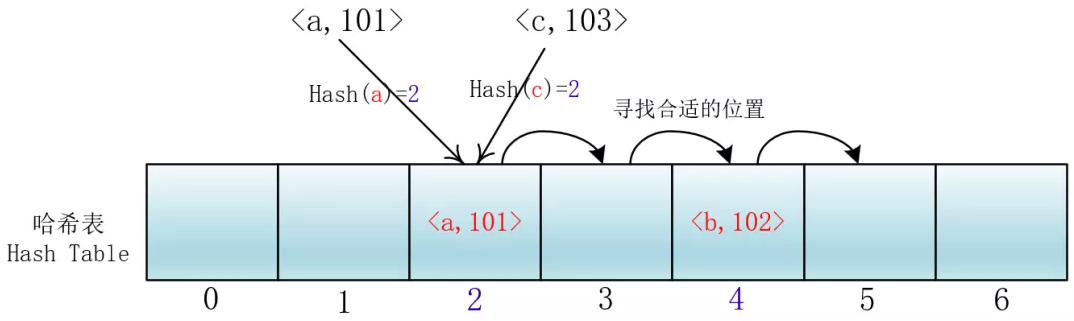
（使用例子：ThreadLocal里面的ThreadLocalMap中的set方法）

java 复制代码 
private void set(ThreadLocal<?> key, Object value) {

    // We don't use a fast path as with get() because it is at
    // least as common to use set() to create new entries as
    // it is to replace existing ones, in which case, a fast
    // path would fail more often than not.

    Entry[] tab = table;
    int len = tab.length;
    int i = key.threadLocalHashCode & (len-1);

    //线性探测的关键代码
    for (Entry e = tab[i];
         e != null;
         e = tab[i = nextIndex(i, len)]) {
        ThreadLocal<?> k = e.get();

        if (k == key) {
            e.value = value;
            return;
        }

        if (k == null) {
            replaceStaleEntry(key, value, i);
            return;
        }
    }

    tab[i] = new Entry(key, value);
    int sz = ++size;
    if (!cleanSomeSlots(i, sz) && sz >= threshold)
        rehash();
}

但是这样会有一个问题，就是随着键值对的增多，会在哈希表里形成连续的键值对。当插入元素时，任意一个落入这个区间的元素都要一直探测到区间末尾，并且最终将自己加入到这个区间内。这样就会导致落在区间内的关键字Key要进行多次探测才能找到合适的位置，并且还会继续增大这个连续区间，使探测时间变得更长，这样的现象被称为"一次聚集（primary clustering）"。

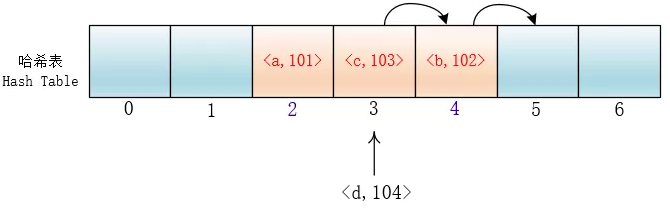
平方探测

在探测时不一个挨着一个地向后探测，可以跳跃着探测，这样就避免了一次聚集。

di=12，-12，22，-22，...，k2，-k2；这种方法的特点是：冲突发生时，在表的左右进行跳跃式探测，比较灵活。虽然平方探测法解决了线性探测法的一次聚集，但是它也有一个小问题，就是关键字key散列到同一位置后探测时的路径是一样的。这样对于许多落在同一位置的关键字而言，越是后面插入的元素，探测的时间就越长。

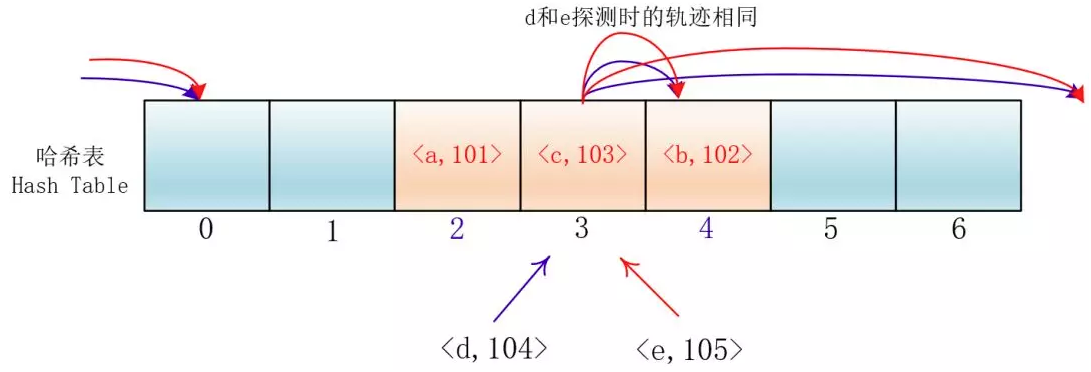
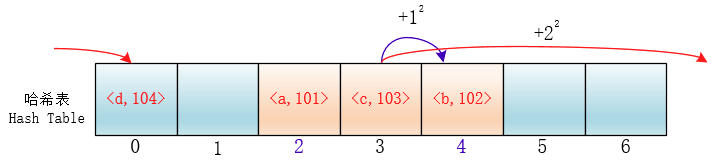
这种现象被称作"二次聚集(secondary clustering)",其实这个在线性探测法里也有。

伪随机探测

di=伪随机数序列；具体实现时，应建立一个伪随机数发生器，（如i=(i+p) % m），生成一个位随机序列，并给定一个随机数做起点，每次去加上这个伪随机数++就可以了。

再散列法

再散列法其实很简单，就是再使用哈希函数去散列一个输入的时候，输出是同一个位置就再次散列，直至不发生冲突位置

缺点：每次冲突都要重新散列，计算时间增加。一般不用这种方式

热门推荐
01KGG转MP3工具|非KGM文件|解密音频02从零安装 LLaMA-Factory 微调 Qwen 大模型成功及所有的坑03YOLOv8入门 | 重要性能衡量指标、训练结果评价及分析及影响mAP的因素【发论文关注的指标】04【SpeedAI科研小助手】2分钟极速解决知网维普重复率、AIGC率过高，一键全文降！文件格式不变，公式都保留的！05YOLOv8目标检测在RK3588部署全过程06西电B测-计算机网络综合实验(含验收问题)07【2025年最新】OpenWrt 更换国内源的指南（图形界面版)08Coze扣子平台完整体验和实践（附国内和国际版对比）09DeepSeek各版本说明与优缺点分析10yolov8实战第五天——yolov8+ffmpg实时视频流检测并进行实时推流——（推流，保姆教学）