【图形学】Blend Shape与RBF插值

目录

• • 前言
  • 概念
  • • 什么是拟合
    • 插值与逼近
    • 插值方法
    • 基函数
  • 数学算法
  • 代码实现

前言

嗨大家，这里是烧酒最喜欢的碎碎念环节。

学RBF是为了搞懂blend shape。但发现RBF不止应用于blend shape，比如常被应用到机器学习。而且这个过程琢磨得我好痛苦呀，我数学太差了，遂写博客记录一下。

所以这篇博客应该也适合 像我一样 数学底子的一般的同学们阅读ww

概念

什么是拟合

给定一组输入x_n，一组输出y_n，已知输入x_i，和对应的输出y_i，求函数f(x)=y。

其中，x可能是n维的数据，y也可能是m维的数据。

---

给一张大家在数学课本上可能见过的、可能有感觉的拟合图：

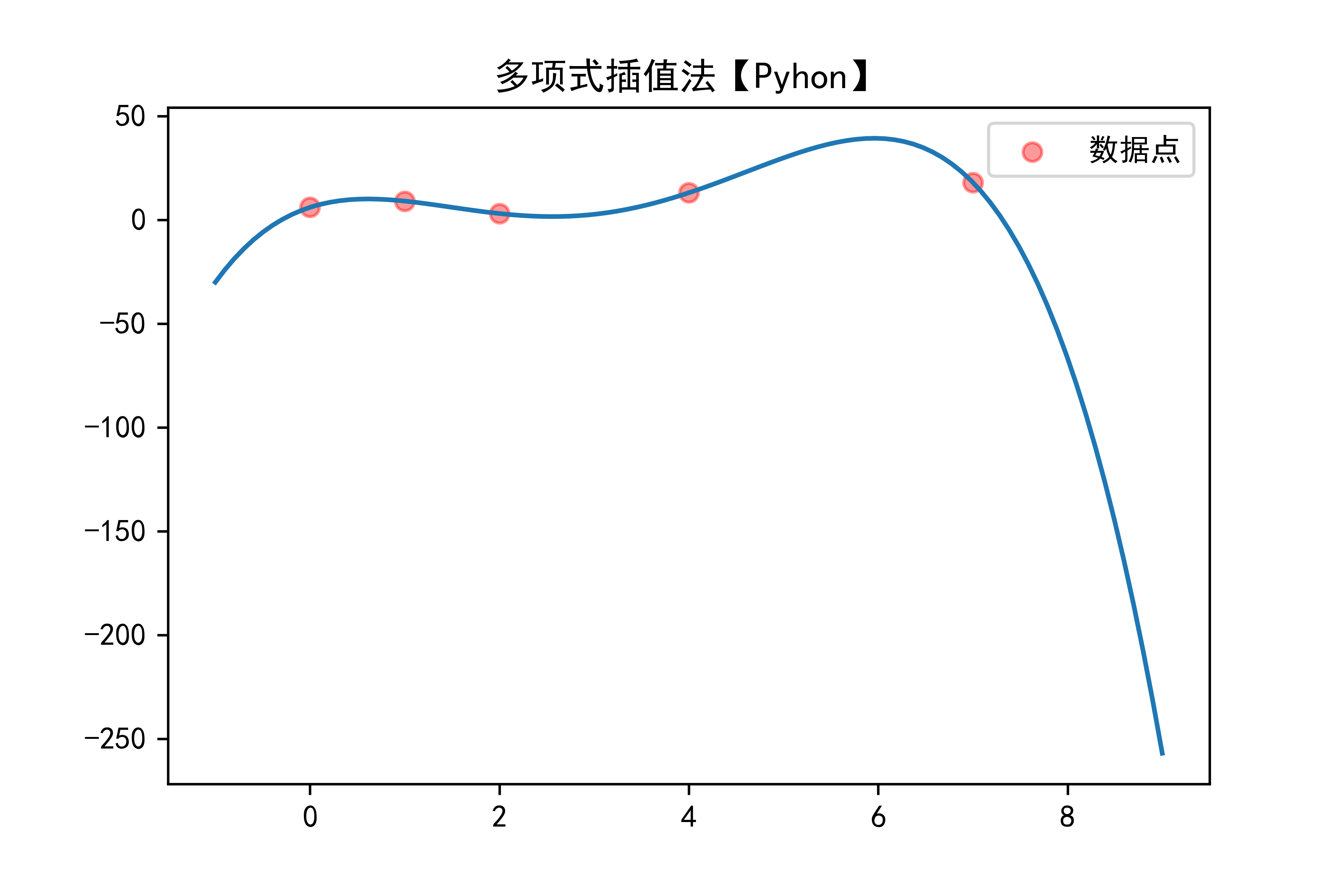
（图是网上随便找的XD）

在这个拟合中，输入是1维的，也就是你所能见到的横坐标。输出也是1维的，也就是你所能见到的纵坐标。

---

再给一张示意图：

在这个拟合中，被操控的小球越靠近方块，就越变成方块的颜色。输入是3维的，也就是被操控的小球的位置，是一个三维空间坐标。输出是3维的，也就是被操控小球的颜色，颜色有三个通道RGB。

---

再讲一个更抽象的例子，blend shape：

在这个拟合中（想不到吧，这么复杂也是拟合），输入是骨骼的旋转角，是3维的；输出是每个姿势的混合权重，有几个姿势，就是几维。

插值与逼近

如果拟合求解得到的函数，能够让每个已知的x都能对应上 它已知的y，那么就是插值 ；如果一部分能对上，一部分对不上 ，就是逼近。

刚刚大家看到的示意图都是插值，这篇文章讲的RBF也是一种插值方法。

然后呢，像这种散点图，就是逼近：

插值方法

1. 分段插值法

这也许是最容易理解的插值方法吧。因为我这几年接触动画比较多，就拿它出来讲了。动画里面很重要的一个工具就是曲线编辑器，要想让动画师k出来的关键帧自动平滑，就会用到三次样条插值。样条插值是一个分段求解的算法：x₁到x₂求一个表达式，x₂到x₃求一个表达式（俩表达式很可能是不同的），然后要保证x₂处是连续的。一次样条插值能保证连线不断，二次样条插值能保证导数连续，三次样条插值能保证二阶导连续。

放个示意图，大家脑补一下~具体的就靠大家查资料啦。

2. 拉格朗日插值法

（来了来了，听到RBF的脚步声了~！）

正如我刚刚所说的，已知输入x_i，和对应的输出y_i，求函数f(x)=y。

如果把函数f(x)=y化解成这样的格式：

f(x) = y₀ L₀(x₀) + ... + y_n L_n(x_n)，

并且，这个L(x)函数要做到，L_n(x_n) = 1并且L_i(x_i≠n) = 0。这样的话，当x取值x_n时，f(x_n) = 0 + ... + y_n * 1 = y_n了。

其中，我们称L_i(x_n)为拉格朗日基函数 ， L i ( x ) = ∏ j = 0 j ≠ i n x − x j x i − x j L_i(x) = \prod_{\substack{j=0 \\ j \neq i}}^{n} \frac{x - x_j}{x_i - x_j} Li(x)=∏j=0j=inxi−xjx−xj。

基函数

更一般地，我们把上述y的位置改为一个系数c，或者也可以叫一个权重w。随便啦，这里我用c表示。然后呢，把拉格朗日公式的L改成更通用的符号ϕ。

于是得到插值函数 f(x_i) = c₀ ϕ₀(x₀) + ... + c_n ϕ_n(x_n) = ∑ i = 0 n c i ϕ i ( x ) \sum_{i=0}^{n} c_i \phi_i(x) ∑i=0nciϕi(x)。其中，我们称 ϕ i ( x ) \phi_i(x) ϕi(x)为基函数。

---

基函数有很多种。上一节我们提到的拉格朗日基函数L(x)就是其中一种，我们这篇文章的主角RBF也是其中一种。

更确切地说，RBF 不是某一个具体的函数，而是一类 函数。这类函数有个特点：满足 ϕ ( r ) = ϕ ( ∥ x − x i ∥ ) \phi(r) = \phi(\|x - x_i\|) ϕ(r)=ϕ(∥x−xi∥)，即，函数的结果与已知点的距离有关。

换一个角度怎么理解呢？也就是说，我已知一组输入点，用RBF插值，求其它输入点的输出。那么，其它输入点，它越"靠近 "某个已知的输入点，那么它的输出就和这个已知的输入点的输出值越像。

所谓的靠近，可以是欧几里得距离，也可以是曼哈顿距离。你可以选用任何其它你觉得适合的、计算距离的方法。

我把刚才的gif再搬出来，帮助大家想象一下~

---

刚刚我提到说，RBF是一类函数。那么，它具体有那些函数表达式呢？

1. 高斯基函数 φ ( r ) = e x p ( − ( r / 2 ∗ ε 2 ) ) φ(r) = exp(-(r / 2 * ε^2)) φ(r)=exp(−(r/2∗ε2))
2. 指数基函数 φ ( r ) = e x p ( − r / ε ) φ(r) = exp(-r / ε) φ(r)=exp(−r/ε)
3. ...

其中： r = ∥ x − x i ∥ r = \|x - x_i\| r=∥x−xi∥

上述提到的函数方法，我们都可以在UE5的pose driver这个动画蓝图节点上找到：

对应的函数在UE源码中一个名为RBFKernel的namespace里：https://github.com/EpicGames/UnrealEngine/blob/release/Engine/Source/Runtime/AnimGraphRuntime/Public/RBF/RBFInterpolator.h

写文章的时候突然发现，截图里的"线性"函数在严格意义上并不是一个RBF基函数。它是一个用钳制的方法凑出来的、和RBF相似的函数。数学公式为：
ϕ ( r ) = { 1 − r σ , 0 ≤ r ≤ σ 0 , r > σ \phi(r) =\begin{cases} 1 - \frac{r}{\sigma}, & 0 \leq r \leq \sigma \\0, & r > \sigma\end{cases} ϕ(r)={1−σr,0,0≤r≤σr>σ

其中：

• r = ∥ x − x i ∥ r = \|x - x_i\| r=∥x−xi∥
• σ \sigma σ 是衰减范围。

所谓的"立方"和"五次"函数，也只是在"线性"的基础上把 r σ \frac{r}{\sigma} σr多乘了几次

哎，还挺巧妙的咧。
找参考代码的时候，还发现一个更骚的。RBF基函数，作者直接用 φ ( r ) = ∣ ∣ x − x i ∣ ∣ φ(r) = ||x - x_i || φ(r)=∣∣x−xi∣∣。

数学算法

已知一组输入点X(i)，有n维；一组对应的输出点Y(i)，有m维；一共有N组数据。

代码实现

from大佬Zhirui Li：
https://github.com/ZhiruiLi/UnityDemoGlob/blob/master/Assets/RBF/RbfMain.cs