【嵌入模型与向量数据库】

特点	描述
高维向量支持	支持数十到上千维的向量存储与计算
相似度检索	支持基于余弦相似度、欧氏距离、点积等方式的Top-K搜索
近似最近邻搜索（ANN）	使用高效算法（如 HNSW、IVF、PQ）实现"近似而快速"的搜索
可扩展性	能够处理上亿甚至上百亿条向量数据
多模态支持	支持图像、文本、音频等多种模态的向量嵌入

四、常见的向量数据库产品

名称	特点
FAISS（Meta）	高性能向量搜索库，适合本地使用
Milvus	开源，分布式，支持亿级向量，适合工业部署
Weaviate	支持文本搜索和语义索引，内置向量生成
Pinecone	云原生，面向生产级应用
Qdrant	支持高效过滤器和payload数据的检索

FAISS 支持的索引类型 vs 相似度

FAISS 索引类型	支持相似度方式	是否需归一化
`IndexFlatL2`	欧氏距离	❌ 否
`IndexFlatIP`	内积（近似余弦）	✅ 是（手动）
`IndexFlatCosine`	✅ 余弦相似度	✅ 自动归一化（新版本才支持）

FAISS : Meta 开源的向量检索引擎 https://github.com/facebookresearch/faiss
Pinecone: 商用向量数据库，只有云服务 The vector database to build knowledgeable AI | Pinecone
Milvus : 开源向量数据库，同时有云服务 Milvus | High-Performance Vector Database Built for Scale
Weaviate: 开源向量数据库，同时有云服务 The AI-native database developers love | Weaviate
Qdrant : 开源向量数据库，同时有云服务 Qdrant - Vector Database - Qdrant
PGVector: Postgres 的开源向量检索引擎 https://github.com/pgvector/pgvector
RediSearch: Redis 的开源向量检索引擎 https://github.com/RediSearch/RediSearch
ElasticSearch 也支持向量检索 Elasticsearch vector search - highly relevant, lightning fast search | Elastic

五、常见向量相似度方法对比

方法名称	取值范围	越小越相似？	特点说明
欧氏距离 (L2)	[0, +∞)	✅ 是	距离越小越相似。对向量长度敏感。
余弦相似度	[-1, 1]	❌ 否	越接近 1 越相似。方向相近即可，不管长度。
内积 (dot product)	任意实数	❌ 否	通常需要归一化后使用，变成余弦相似度。

六、应该用哪种

场景	推荐相似度类型	理由
文本检索 / 语义搜索	余弦相似度 or 内积（需归一化）	语义相似的句子方向一致，即便长度不同也应视为相似。
数值空间距离计算	欧氏距离（L2）	更注重"几何距离"本身。
图像、传感器数据	L2 / 内积	嵌入空间常是连续向量域，L2 更合适。

代码示例

python 复制代码

import numpy as np

# 假设有两个向量
vec1 = np.array([0.1, 0.3, 0.5])
vec2 = np.array([0.2, 0.1, 0.7])

# 欧氏距离
euclidean = np.linalg.norm(vec1 - vec2)

# 曼哈顿距离
manhattan = np.sum(np.abs(vec1 - vec2))

# 余弦相似度
cosine = np.dot(vec1, vec2) / (np.linalg.norm(vec1) * np.linalg.norm(vec2))

print(f"欧氏距离: {euclidean:.4f}")
print(f"曼哈顿距离: {manhattan:.4f}")
print(f"余弦相似度: {cosine:.4f}")

运行结果

欧氏距离: 0.3000

曼哈顿距离: 0.5000

余弦相似度: 0.9201

七、向量数据库的核心逻辑

🔍 示例任务：查找与这句话最相似的一句话

🟢 查询语句：

"我今天想去看电影。"

被模型（如 BERT）转换成一个 768 维向量：
[0.12, -0.34, 0.56, ..., 0.87]

🗂 向量数据库中预存了大量句子的向量，比如：

原始句子	向量表示（768维）
"晚上看个电影放松一下吧。"	`[0.13, -0.33, 0.57, ..., 0.88]`
"我今天不太想出门。"	`[0.01, -0.55, 0.24, ..., 0.39]`
"今天天气很好。"	`[0.45, 0.22, 0.18, ..., 0.72]`

📌 向量数据库通过余弦相似度 等算法，找出最相似的向量（Top-K），再返回对应的句子。

八、图示：向量空间中的相似度搜索

想象每个句子被映射到一个三维空间中的点（实际是高维空间）：

复制代码

🧲 目标是：找到距离查询点最近的几个点 ------ 这就是向量数据库做的事！

九、实际案例：文本语义检索

你构建了一个问答系统，用户输入：

"怎么注册公司的营业执照？"

系统会将这个问题转为向量，然后在知识库中查找语义最接近的答案，比如：

"如何办理工商注册？"
"注册公司需要准备哪些资料？"
"去哪个地方办营业执照？"

向量数据库会返回这些"语义相似"的文本，而不只是关键词匹配。

🧠 这就是语义搜索 vs 关键词搜索的区别。

十、实际案例：图像搜索

你上传一张猫的照片，系统会在数据库中返回类似的图片：

🐱 颜色相近的猫
🐈 姿势相似的猫
🐾 背景相近的猫图

原因是：图像也可以转成向量，向量数据库进行相似度查找。

十一、总结图：向量数据库流程

复制代码

   原始数据（文本/图片/音频）
        ↓
   向量模型生成 embedding
        ↓
   向量入库（Milvus, FAISS, Pinecone等）
        ↓
   用户输入查询 → 同样转换成向量
        ↓
   在向量空间中找最近的K个邻居（ANN）
        ↓
   返回原始内容（文本、图片、视频等）

十二、 faiss向量数据代码用例

说明

**1、选用向量模型：**阿里百炼的文本向量模型（text-embedding-v1）；

2、运行条件： 需要有百炼控制台的APIkey；

3、查看（选择）其它向量模型： 百炼控制台；

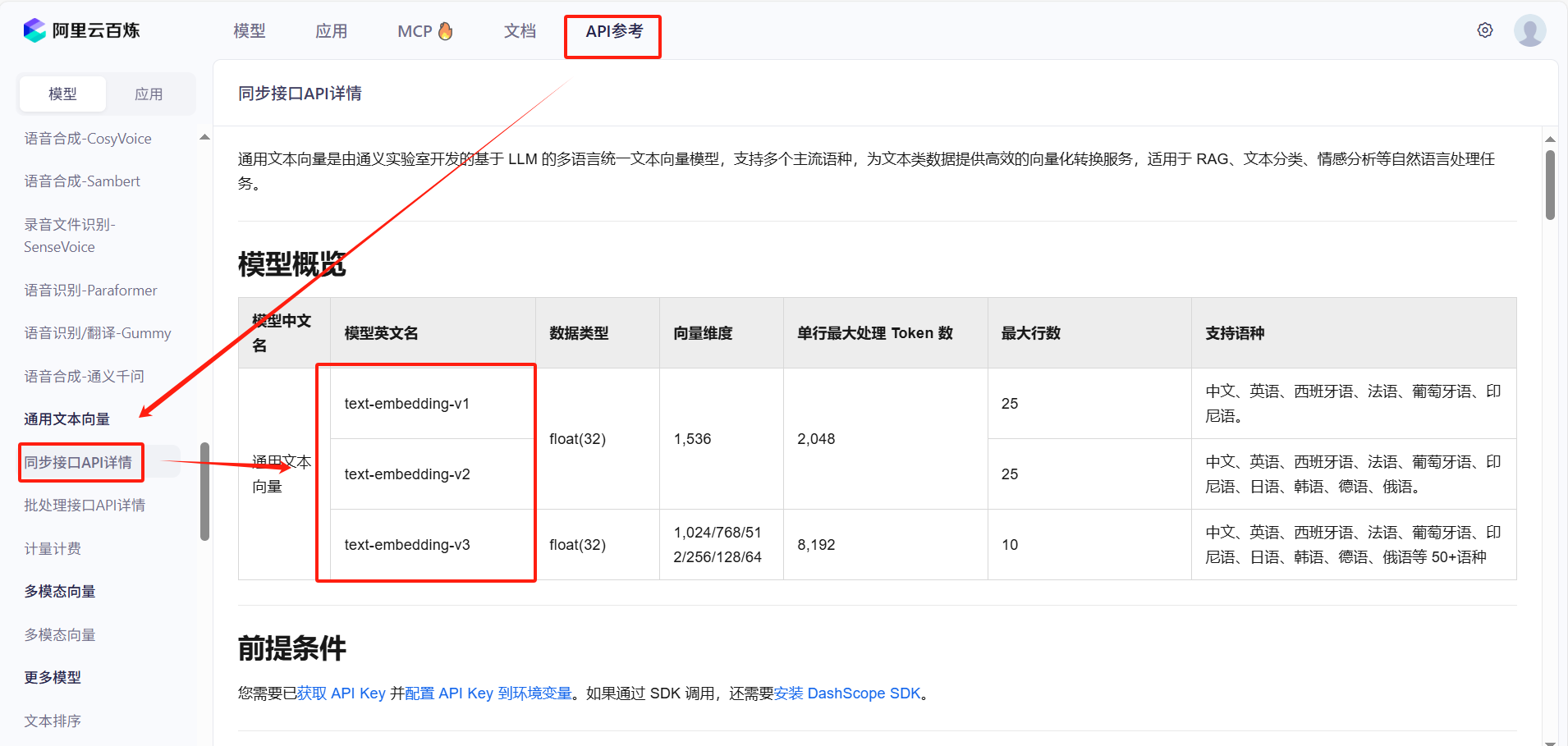
该图是百炼提供的3种文本向量模型

文件结构

semantic_search_demo/

├── main.py # 主程序

├── documents.txt # 示例语料库（你要搜索的内容）

├── requirements.txt # 依赖库

documents.txt

这个作为知识库示例

注册公司需要准备身份证、注册地址、公司章程等材料。

营业执照由工商局颁发，需要填写申请表。

税务登记是注册公司的后续步骤。

开公司银行账户需要营业执照和法人身份证。

你可以在线申请营业执照。

main.py（简化版）

python 复制代码

import faiss
import dashscope
import os
import numpy as np
from tqdm import tqdm

# 设置 API KEY（你也可以改为用环境变量）
dashscope.api_key = os.getenv("DASHSCOPE_API_KEY")

# 获取当前脚本所在目录的绝对路径
BASE_DIR = os.path.dirname(os.path.abspath(__file__))
DOC_PATH = os.path.join(BASE_DIR, "documents.txt")

# 载入文档
if not os.path.exists(DOC_PATH):
    raise FileNotFoundError(f"未找到文件：{DOC_PATH}")

with open(DOC_PATH, "r", encoding="utf-8") as f:
    docs = [line.strip() for line in f.readlines() if line.strip()]

# 使用阿里百炼嵌入模型
def get_embedding(text):
    rsp = dashscope.TextEmbedding.call(
        model="text-embedding-v1",
        input=text
    )
    if rsp.status_code == 200:
        return rsp.output['embeddings'][0]['embedding']
    else:
        raise ValueError(f"❌ 嵌入失败: {rsp.message}")

# 生成文档向量
print("🔍 正在生成文档向量...")
doc_embeddings = [get_embedding(doc) for doc in tqdm(docs)]

# 建立 FAISS 索引
dim = len(doc_embeddings[0])
index = faiss.IndexFlatL2(dim)
index.add(np.array(doc_embeddings).astype("float32"))

# 查询函数
def search(query, top_k=3):
    q_embedding = get_embedding(query)
    D, I = index.search(np.array([q_embedding]).astype("float32"), top_k)
    return [(docs[i], D[0][j]) for j, i in enumerate(I[0])]

# 主循环
if __name__ == "__main__":
    while True:
        q = input("\n请输入查询（输入 'exit' 退出）：\n> ")
        if q.lower() == "exit":
            break
        results = search(q)
        print("\n🔍 最相似的段落：")
        for i, (text, score) in enumerate(results):
            print(f"{i+1}. {text}  （距离：{score:.4f}）")

运行结果

🔍 正在生成文档向量...

100%|█████████████████████████████████████| 5/5 [00:09<00:00, 1.90s/it]

请输入查询（输入 'exit' 退出）：

> 一个公司的创建需要具备什么条件

🔍 最相似的段落：

注册公司需要准备身份证、注册地址、公司章程等材料。（距离：6633.3623）

开公司银行账户需要营业执照和法人身份证。（距离：8122.5732）

营业执照由工商局颁发，需要填写申请表。（距离：9337.1758）

请输入查询（输入 'exit' 退出）：

>三里屯怎么走

🔍 最相似的段落：

注册公司需要准备身份证、注册地址、公司章程等材料。（距离：15391.9512）

税务登记是注册公司的后续步骤。（距离：15656.2275）

你可以在线申请营业执照。（距离：16183.6201）

请输入查询（输入 'exit' 退出）：

> 注册公司需要准备什么材料

🔍 最相似的段落：

注册公司需要准备身份证、注册地址、公司章程等材料。（距离：1627.7302）

营业执照由工商局颁发，需要填写申请表。（距离：5437.8076）

开公司银行账户需要营业执照和法人身份证。（距离：5667.3779）

main.py(优化版)

python 复制代码

import faiss
import os
import numpy as np
from tqdm import tqdm
import dashscope
from dotenv import load_dotenv

# 加载 .env 文件中的 API Key
load_dotenv()
dashscope.api_key = os.getenv("DASHSCOPE_API_KEY")

# 获取当前脚本所在目录的路径
BASE_DIR = os.path.dirname(os.path.abspath(__file__))
DOC_PATH = os.path.join(BASE_DIR, "documents.txt")

# 载入文档
if not os.path.exists(DOC_PATH):
    raise FileNotFoundError(f"未找到文件：{DOC_PATH}")

with open(DOC_PATH, "r", encoding="utf-8") as f:
    docs = [line.strip() for line in f.readlines() if line.strip()]

# 获取阿里百炼的向量
def get_embedding(text):
    rsp = dashscope.TextEmbedding.call(
        model="text-embedding-v1",  # 阿里模型名
        input=text,
    )
    return rsp.output["embeddings"][0]["embedding"]

# 向量归一化函数
def normalize(vec):
    norm = np.linalg.norm(vec)
    return vec / norm if norm > 0 else vec

# 生成文档向量
print("🔍 正在生成文档向量...")
doc_embeddings = [normalize(get_embedding(doc)) for doc in tqdm(docs)]

# 建立 FAISS 余弦相似度索引（内积模式）
dim = len(doc_embeddings[0])
index = faiss.IndexFlatIP(dim)
index.add(np.array(doc_embeddings).astype("float32"))

# 计算欧几里得距离（欧式距离）
def euclidean_distance(vec1, vec2):
    return float(np.linalg.norm(np.array(vec1) - np.array(vec2)))

# 查询函数：使用余弦相似度
def search(query, top_k=3):
    q_embedding = normalize(get_embedding(query))

    similarities = []
    for doc, doc_emb in zip(docs, doc_embeddings):
        # 计算余弦相似度
        cosine_sim = float(np.dot(q_embedding, doc_emb))
        # 计算欧几里得距离
        dist = euclidean_distance(q_embedding, doc_emb)

        similarities.append((doc, cosine_sim, dist, doc_emb))

    # 按余弦相似度排序
    similarities.sort(key=lambda x: x[1], reverse=True)
    top_results = similarities[:top_k]

    print("\n🔍 查询向量：")
    print(np.round(q_embedding, 4).tolist())

    print("\n📊 相似文档向量、余弦相似度 & 欧式距离：")
    for i, (doc, sim, dist, vec) in enumerate(top_results):
        print(f"\n{i+1}. 文本内容：{doc}")
        print(f"   文档向量：{np.round(vec, 4).tolist()}")
        print(f"   余弦相似度：{sim:.4f}")
        print(f"   欧式距离：{dist:.4f}")

    return [(doc, sim, dist) for doc, sim, dist, _ in top_results]


# 主循环
if __name__ == "__main__":
    while True:
        q = input("\n请输入查询（输入 'exit' 退出）：\n> ")
        if q.lower() == "exit":
            break
        results = search(q)
        print("\n🔍 最相似的段落（按余弦相似度降序）：")
        for i, (text, sim, dist) in enumerate(results):
            print(f"{i+1}. {text}  （余弦相似度：{sim:.4f}，欧式距离：{dist:.4f}）")

运行结果

🔍 正在生成文档向量...

100%|█████████████████████████████████████████████████████████████████████████████████████████████████████| 5/5 [00:12<00:00, 2.59s/it]

请输入查询（输入 'exit' 退出）：

> 你好

🔍 查询向量：
$0.0026, -0.0312, 0.0114, 0.0236, -0.0029, 0.0034, 0.0251, -0.0333, -0.0135, 0.0028, -0.0288, 0.0582, 0.0263, -0.0033, 0.0137, -0.0047, -0.0317, 0.016, -0.0047, 0.0211, -0.0313, -0.0203, 0.0066, -0.0228, 0.0292, -0.0183, 0.0028, 0.0084, -0.0164, 0.0071...$
📊 相似文档向量、余弦相似度 & 欧式距离：

文本内容：你可以在线申请营业执照。

文档向量：[0.0312, 0.0475, 0.0324, 0.0472, -0.0346, 0.0171, -0.0325, 0.028, -0.0763, -0.0216, -0.0158, 0.0121, -0.0084, -0.0194, 0.0368, -0.0105, 0.0095, -0.0155, 0.0385, 0.013, -0.0147, 0.001, 0.0547, 0.0259, 0.0132, 0.0262, -0.0585, 0.0146, -0.0198, 0.016, ... ]

余弦相似度：0.1997

欧式距离：1.2652

文本内容：注册公司需要准备身份证、注册地址、公司章程等材料。

文档向量：[0.0006, 0.0363, 0.0236, 0.0462, -0.0021, 0.0076, -0.0199, 0.027, -0.0587, -0.0176, -0.0289, -0.0134, 0.0296, -0.0566, 0.0102, -0.006, 0.0052, -0.0242, 0.0255, -0.046, -0.0065, 0.0107, 0.0173, 0.0214, -0.0075, 0.0027, -0.0233, -0.014, -0.0467, 0.0144, ]

余弦相似度：0.1473

欧式距离：1.3059

文本内容：开公司银行账户需要营业执照和法人身份证。

文档向量：[0.0007, 0.0148, 0.107, 0.009, -0.0025, 0.0103, -0.0273, 0.0553, -0.0794, -0.0432, -0.0285, -0.0105, 0.0291, -0.0292, 0.0212, -0.0296, 0.0196, -0.0294, 0.0092, -0.0325, 0.0117, -0.0071, -0.0013, 0.0267, -0.0065, 0.0112, -0.044, 0.0127, -0.0102...]

余弦相似度：0.1357

欧式距离：1.3148

🔍 最相似的段落（按余弦相似度降序）：

你可以在线申请营业执照。（余弦相似度：0.1997，欧式距离：1.2652）

注册公司需要准备身份证、注册地址、公司章程等材料。（余弦相似度：0.1473，欧式距离：1.3059）

开公司银行账户需要营业执照和法人身份证。（余弦相似度：0.1357，欧式距离:1.3148）