深入浅出了解生成模型-2：VAE模型原理以及代码实战

Big-Yellow-J2025-05-18 21:30

From: https://www.big-yellow-j.top/posts/2025/05/11/VAE.html

前文已经介绍了GAN的基本原理以及代码操作，本文主要介绍VAE其基本原理以及代码实战

VAE or AE

介绍VAE之前了解两个概念：AE（AutoEncoder，自编码器）和VAE（Variational Autoencoder，变自编码器）。AE ：自编码器是一种无监督学习神经网络，旨在通过将输入数据压缩到一个低维表示（编码），然后从该表示重建输入数据（解码），来学习数据的特征表示。VAE ：变分自编码器是自编码器的扩展，结合了概率模型和深度学习，通过引入变分推理使潜在空间具有概率分布特性，适合生成任务。
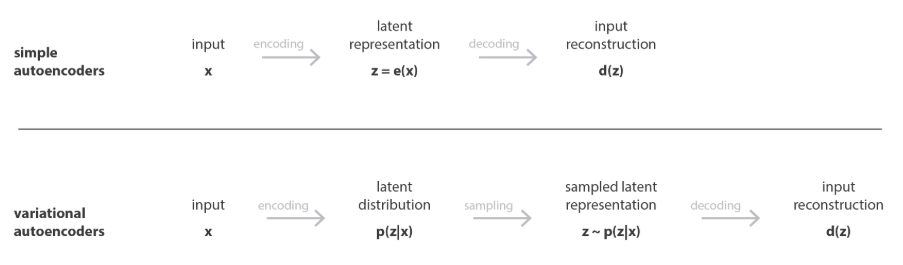
AE 的数学描述对于输入 \(x\)通过编码器将输入映射到 低纬空间 \(z=f(x)\)而后通过解码器得到输出：\(\hat{x}=g(x)\)
VAE 的数学描述对于输入 \(x\)通过编码器将输入映射成 概率分布 \(q(z\vert x)\)，假设为高斯分布，输出 𝜇和 𝜎，从 \(q(z\vert x)\)采样 \(z\)而后通过 \(z=\mu+ \sigma+ \epsilon\) 其中 \(\epsilon \in N(0,1)\)，而后通过采样得到的\(z\)重新构建输入，生成\(p(x\vert z)\)

前者不适合对于图片进行生成而后者则是更加适合图像生成，这是因为AE将输入映射到一个低纬空间z这个低纬空间并没有明确的结构，进而就可能不适合去生成新的数据，而VAE之所以可以用于生成新的数据是，比如说对于图像数据（比如说：猫）如果知道其分布特征，就可以直接通过分布特征去构建一个新的图像

VAE（Variational Autoencoder）

上面简单介绍了VAE数学描述这里重新再描述一下其数学描述（涉及到比较多贝叶斯统计相关内容）：

1.基本框架

VAE 是一种生成模型，目标是学习数据的概率分布 p(x)，让模型能生成类似真实数据的新样本 ，想象我们要制作各种蛋糕（数据 \(x\)），但不知道蛋糕的"秘方"（潜在变量 \(z\)）。假设所有蛋糕组成数据集 \(X = {x_1, \dots, x_n}\)，每种蛋糕（如巧克力蛋糕或水果蛋糕）背后有独特的秘方。VAE 通过学习秘方的分布和生成过程，制造出逼真的蛋糕。
秘方 ：VAE 假设秘方 \(z\) 服从标准正态分布，即先验分布 \(p(z) = \mathcal{N}(0, I)\)。这意味着大多数秘方是"普通"的，围绕平均值分布。
生成蛋糕（解码器） ：给定秘方 \(z\)，VAE 使用一个"蛋糕机"（解码器，参数 \(\theta\)）生成蛋糕 \(x\)。解码器建模条件分布 \(p_\theta(x\vert z) = \mathcal{N}(x; \mu_\theta(z), \sigma_\theta^2(z))\)，表示从 \(z\) 生成 \(x\) 的概率。
猜测秘方（编码器） ：直接从蛋糕 \(x\) 反推秘方（后验分布 \(p_\theta(z\vert x)=\frac{p_\theta(x,z)}{p_\theta(x)}=\frac{p_\theta(x\vert )p(z)}{p_\theta(x)}\)）很困难（因为我的变量是一个高维的，换句说法就是我的蛋糕他有千奇百怪种组合）。既然如此就只需要将制造蛋糕的组合分解，分解成低维的变量 \(z\)（也就是上面提到的 秘方 ）然后我去计算下面一个联合分布（\(p(x,z)\)）：

\[p_\theta(x) =\int p_\theta(x\vert z)p(z)dz \]

不过就算上面积分会存在困难即使你将蛋糕分解成不同的 潜在变量 但是这些潜在变量种类也是很多的（蛋糕奶油、加不加巧克力等等）那么上面的联合分布就会变成：

\[\int p_\theta(x\vert z)p(z)dz = \int_{z_1} ... \int_{z_d}p_\theta(x\vert z)p(z)d_{z_1}...d_{z_d} \]

这种高维积分没有解析解，数值积分计算复杂度随维度指数增长，因此在VAE 引入一个"猜测机"（编码器，也就是一个神经网络，参数 \(\varphi\)），用变分分布：

\[q_\varphi(z\vert x) = \mathcal{N}(z; \mu_\varphi(x), \text{diag}(\sigma_\varphi^2(x))) \]

近似后验分布，估计可能的秘方也就是去估算我们的：\(p_\theta(z\vert x)\)

再去引入新的参数 \(\varphi\) 不还是很难计算吗？似乎是这么一回事，但是回顾我们需要解决的问题：\(p_\theta(z\vert x)=\frac{p_\theta(x,z)}{p_\theta(x)}=\frac{p_\theta(x\vert z)p(z)}{p_\theta(x)}\) 分子分母三项都是很难计算的那么也就意味着如果要通过 \(x\) "推算" \(z\) 基本就是很难解决的问题，那么"干脆"不去计算用神经网络进行"模拟"也就是说 \(p_\theta(z\vert x) ≈ p_\varphi(z\vert x)\)

大致总结一下就是：VAE的主要的任务就是，最开始的数据集里面，我希望通过对这个数据的潜在分布进行学习，如果我模型学会了各类数据的分布，那么就可以通过这些分布去进一步生成新的数据。

2.损失函数构建

了解模型基本框架之后就需要对整个模型的参数进行求解，正如上面所述对于数据集分布 \(p_\theta(x)\) 的计算我们通过构建一个和 \(z\)的联合分布，因此整个过程计算如下：

\[\begin{align} \log p_{\theta}(x) &= \log p_{\theta}\left(x\right) \tag{1} \\ &= \log p_{\theta}\left(x\right)\int q_{\varphi}(z\vert x)dz \tag{2} \\ &= \int\log p_{\theta}\left(x\right)q_{\varphi}(z\vert x)dz \tag{3} \\ &= \mathbb{E}{q{\varphi}(\mathbf{Z}\vert\mathbf{X})}[\log p_{\theta}(\mathbf{x})] \tag{4} \\ &= \mathbb{E}{q{\varphi}(\mathbf{Z}\vert\mathbf{X})}\left[\log\frac{p_{\theta}(\mathbf{x},\mathbf{z})}{p_{\theta}(\mathbf{z}\vert\mathbf{x})}\right] \tag{5} \\ &= \mathbb{E}{q{\varphi}(\mathbf{Z}\vert\mathbf{X})}\left[\log\frac{p_{\theta}(\mathbf{x},\mathbf{z})q_{\varphi}(\mathbf{z}\vert\mathbf{x})}{p_{\theta}(\mathbf{z}\vert\mathbf{x})q_{\varphi}(\mathbf{z}\vert\mathbf{x})}\right] \tag{6} \\ &= \mathbb{E}{q{\varphi}(\mathbf{z}\vert\mathbf{x})}\left[\log\frac{p_{\theta}(\mathbf{x},\mathbf{z})}{q_{\varphi}(\mathbf{z}\vert\mathbf{x})}\right] + \mathbb{E}{q{\varphi}(\mathbf{z}\vert\mathbf{x})}\left[\log\frac{q_{\varphi}(\mathbf{z}\vert\mathbf{x})}{p_{\theta}(\mathbf{z}\vert\mathbf{x})}\right] \tag{7} \\ &= \mathbb{E}{q{\varphi}(\mathbf{z}\vert\mathbf{x})}\left[\log\frac{p_{\theta}(\mathbf{x},\mathbf{z})}{q_{\varphi}(\mathbf{z}\vert\mathbf{x})}\right] + \underbrace{D_{\mathrm{KL}}\left(q_{\varphi}(\mathbf{z}\vert\mathbf{x}) \parallel p_{\theta}(\mathbf{z}\vert\mathbf{x})\right)}{\geq 0} \tag{8} \\ &\geq \mathbb{E}{q_{\varphi}(\mathbf{z}\vert\mathbf{x})}\left[\log\frac{p_{\theta}(\mathbf{x},\mathbf{z})}{q_{\varphi}(\mathbf{z}\vert\mathbf{x})}\right] \quad (\text{ELBO}) \tag{9} \end{align} \]

其中 \(\text{ELBO}\)也就是所谓的变分下界

（1-3）上面介绍对于联合分布 \(p_\theta(x) =\int p_\theta(x\vert z)p(z)dz\) 计算存在困难，因此替换为 \(p_\theta(x) =\int p_\varphi(x\vert z)p(z)dz\)；（4-7）直接就是贝叶斯公式和一些基本变形；（8）最后一项就是 \(KL\)散度。最后上面公式就可以写成：

\[\begin{aligned} \log p_{\theta}(x)\geq E_{q_{\varphi}(\mathbf{z}|\mathbf{x})}\left[\log\frac{p_{\theta}(\mathbf{x},\mathbf{z})}{q_{\varphi}(\mathbf{z}|\mathbf{x})}\right] & =E_{q_{\varphi}(\mathbf{Z}|\mathbf{X})}\left[\log\frac{p_{\theta}(\mathbf{x}|\mathbf{z})p(\mathbf{z})}{q_{\varphi}(\mathbf{z}|\mathbf{x})}\right] \\ & =E_{q_{\varphi}(\mathbf{Z}|\mathbf{X})}[\log p_{\theta}(\mathbf{x}|\mathbf{z})]+E_{q_{\varphi}(\mathbf{Z}|\mathbf{X})}\left[\log\frac{p(\mathbf{z})}{q_{\varphi}(\mathbf{z}|\mathbf{x})}\right] \\ & =E_{q_{\varphi}(\mathbf{Z}|\mathbf{X})}[\log p_{\theta}(\mathbf{x}|\mathbf{z})]-D_{KL}\left(q_{\varphi}(\mathbf{z}|\mathbf{x})\|p_{\theta}(\mathbf{z})\right) \end{aligned} \]

那么我们的损失函数就是（最大化下面计算）：

\[L(\theta, \varphi,x)= E_{q_{\varphi}(\mathbf{z}|\mathbf{x})}\left[\log\frac{p_{\theta}(\mathbf{x},\mathbf{z})}{q_{\varphi}(\mathbf{z}|\mathbf{x})}\right]=E_{q_{\varphi}(\mathbf{Z}|\mathbf{X})}[\log p_{\theta}(\mathbf{x}|\mathbf{z})]-D_{KL}(q_{\varphi}(\mathbf{z}|\mathbf{x})\|p_{\theta}(\mathbf{z})) \]

在深度学习中自然就会直接用 梯度下降 的方法去优化参数，下面推荐借鉴：https://arxiv.org/pdf/1906.02691 中的描述

参数求解之前引入最开始定义的几个变量：

\[q_\varphi(z\vert x) = \mathcal{N}(z; \mu_\varphi(x), \text{diag}(\sigma_\varphi^2(x))) \qquad p_\theta(x\vert z) = \mathcal{N}(x; \mu_\theta(z), \sigma_\theta^2(z)) \]

2.1 参数 \(\theta\) 计算

对于 \(\theta\)参数可以得到：

\[\begin{align} \nabla_{\theta} \mathcal{L}(x,\theta,\varphi) &= \nabla_{\theta} \mathbb{E}{q\varphi(z|x)} \left[ \log p_\theta(x,z) - \log q_\varphi(z|x) \right] \\ &= \mathbb{E}{q\varphi(z|x)} \left[ \nabla_{\theta} (\log p_\theta(x,z) - \log q_\varphi(z|x)) \right] \\ &\approx \nabla_{\theta} (\log p_\theta(x,z) - \log q_\varphi(z|x)) \\ &= \nabla_{\theta} (\log p_\theta(x,z)) \end{align} \]

（1-2）也需要注意之所以可以将梯度拿到期望里面（直接借鉴 grok里面解释），另外一点在计算梯度时候将 KL散度拿掉这是因为在KL计算中第一部分参数为 \(\varphi\)，而第二部分参数 \(p_\theta(x)\) 我们实现定义他是一个简单的标准正态分布：\(\mathcal{N}(0, I)\)

（3）这是因为在后面一项中参数是 \(\varphi\) 因此计算梯度直接为0因此就可以拿掉，对于下面公式：

\[\mathbb{E}{q\varphi(z|x)} [\nabla_{\theta} (\log p_\theta(x,z)] \rightarrow \nabla_{\theta} (\log p_\theta(x,z)) \]

一个容易接受的说法：可以直接通过蒙特卡洛方法，通过从分布中抽取少量样本（甚至单样本）来近似期望值。因此对于期望

\[\mathbb{E}{q\varphi(z\vert x)}[ \nabla_\theta \log p_\theta(x, z)] \approx \frac{1}{S} \sum_{s=1}^S \nabla_\theta \log p_\theta(x, z) \]

计算，可以去通过从 \(q_\varphi(z\vert x)\) 进行抽样，当 \(S=1\) 时候就直接变成单个样本去近似整个期望。（单样本估计的方差可以通过SGD的多次迭代和批量数据的处理来缓解，模型会在优化过程中逐渐收敛到一个较好的解（通常是局部最优或接近全局最优））

2.2 参数 \(\varphi\) 计算

对于参数 \(\varphi\)不能直接像上面计算一样直接将 \(\nabla\) 拿到期望里面（期望和分布都依赖参数 \(\varphi\)）也就是 论文 里面提到的下面公式不成立：

\[\begin{equation} \nabla_{\varphi} \mathcal{L}{\theta, \varphi}(x) = \nabla{\varphi} \mathbb{E}{q{\varphi}(z|x)} \left[ \log p_{\theta}(x, z) - \log q_{\varphi}(z|x) \right] \neq \mathbb{E}{q{\varphi}(z|x)} \left[ \nabla_{\varphi} \left( \log p_{\theta}(x, z) - \log q_{\varphi}(z|x) \right) \right] \end{equation} \]

下面是成立的并且可以直接求导变为0

\[\mathbb{E}{q\varphi(z\vert x)}[\nabla_\theta \log p_\theta(x, z)] \]

既然如此那么就直接涌入一个随机变量 \(\epsilon\) 将最开始的 \(z \in q_{\varphi}(z\vert x)\) 转化为：\(z=g(\epsilon,\varphi,x)\)，回顾最开始定义的损失函数：

\[L(\theta,\varphi,x) = E_{q_{\varphi}(\mathbf{z}|\mathbf{x})}[\log p_{\theta}(\mathbf{x}|\mathbf{z})]-D_{KL}(q_{\varphi}(\mathbf{z}|\mathbf{x})\|p_{\theta}(\mathbf{z})) \]

  • 第一部重构项计算 ：\(E_{q_{\varphi}(\mathbf{z}\vert \mathbf{x})}[\log p_{\theta}(\mathbf{x}\vert\mathbf{z})]\)

因为通过引入了随机变量 \(\epsilon\)因此上面公式可以变为：\(E_\epsilon[\log p_{\theta}(\mathbf{x}\vert\mathbf{z})]\)，那么对于其梯度进行计算得到：

\[\nabla_{\varphi} \mathbb{E}{q{\varphi}(z\vert x)} \left[ \log p_{\theta}(\mathbf{x}\vert \mathbf{z}) \right] = \mathbb{E}{p(\epsilon)} \left[ \nabla{\varphi} \log p_{\theta}(\mathbf{x}|\mathbf{z}) \right] = \nabla_{\varphi} \log p_{\theta}(\mathbf{x}|\mathbf{z}) \]

是不是可以直接让其变成0？还是不行因为里面变量 \(z\)的分布还是依赖我们的变量 \(\varphi\)（最开始我们假设了\(\mathcal{N}(z; \mu_\varphi(x), \text{diag}(\sigma_\varphi^2(x)))\)）对于最后的结果就和最开始的 \(\theta\)求解一样可以直接通过蒙特卡洛模拟来进行计算，也就是：

\[\nabla_{\varphi} \mathbb{E}{q{\varphi}(z|x)} \left[ \log p_{\theta}(\mathbf{x}|\mathbf{z}) \right]≈\frac{1}{S}\sum_{s=1}^{S}log p_\theta(x\vert z) \]

  • 第二部分KL散度计算 ：\(D_{KL}(q_{\varphi}(\mathbf{z}\vert \mathbf{x})\vert p_{\theta}(\mathbf{z}))\)

\(D_{KL}\left(q_{\varphi}(\mathbf{z}\vert \mathbf{x})\vert p_{\theta}(\mathbf{z})\right)=E_{q_{\varphi}(\mathbf{Z}\vert \mathbf{X})}\left[\log\frac{q_{\varphi}(\mathbf{z}\vert \mathbf{x})}{p_\theta(\mathbf{z})}\right]\)

\[\begin{align} \nabla_\varphi D_{KL}(q_\varphi(\mathbf{z}|\mathbf{x}) \| p_\theta(\mathbf{z})) &= \nabla_\varphi \int q_\varphi(\mathbf{z}|\mathbf{x}) [\log q_\varphi(\mathbf{z}|\mathbf{x}) - \log p_\theta(\mathbf{z})] d\mathbf{z} \\ &= \int \left[ \nabla_\varphi q_\varphi(\mathbf{z}|\mathbf{x}) [\log q_\varphi(\mathbf{z}|\mathbf{x}) - \log p_\theta(\mathbf{z})] + q_\varphi(\mathbf{z}|\mathbf{x}) \cdot \frac{\nabla_\varphi q_\varphi(\mathbf{z}|\mathbf{x})}{q_\varphi(\mathbf{z}|\mathbf{x})} \right] d\mathbf{z} \\ &= \int \nabla_\varphi q_\varphi(\mathbf{z}|\mathbf{x}) \left[ \log q_\varphi(\mathbf{z}|\mathbf{x}) - \log p_\theta(\mathbf{z}) + 1 \right] d\mathbf{z} \\ &= \int q_\varphi(\mathbf{z}|\mathbf{x}) \left[ \nabla_\varphi \log q_\varphi(\mathbf{z}|\mathbf{x}) \right] \left[ \log q_\varphi(\mathbf{z}|\mathbf{x}) - \log p_\theta(\mathbf{z}) + 1 \right] d\mathbf{z} \\ &= \mathbb{E}{q{\varphi}(\mathbf{z}|\mathbf{x})} \left[ \left( \log q_\varphi(\mathbf{z}|\mathbf{x}) - \log p_\theta(\mathbf{z}) + 1 \right) \nabla_\varphi \log q_\varphi(\mathbf{z}|\mathbf{x}) \right] \\ &\approx \frac{1}{L} \sum_{l=1}^L \left[ \left( \log q_\varphi(\mathbf{z}^{(l)}|\mathbf{x}) - \log p_\theta(\mathbf{z}^{(l)}) + 1 \right) \nabla_\varphi \log q_\varphi(\mathbf{z}^{(l)}|\mathbf{x}) \right], \quad \mathbf{z}^{(l)} \sim q_\varphi(\mathbf{z}|\mathbf{x}) \end{align} \]

上面公式中第2项：直接通过求导的乘法法则，对于括号里面内容求导过程中:第二项 \(logp_\theta(z)\)和 \(\varphi\)无关因此直接等于0，第4项：\(\nabla_\varphi q_\varphi(z \vert x)=q_\varphi(z\vert x)\nabla_ \varphi logq_\varphi(z\vert x)\)，最后两项就是直接改写为期望然后通过蒙特卡洛计算得到结果。

VQ-VAE

https://arxiv.org/pdf/1711.00937

注意主要简单介绍一下其基本原理，VQ-VAE主要是为了解决VAE在生成样本模糊问题，通过向量量化将编码器的输出映射到离散的码本（codebook）中。这种离散化可以更好地捕捉数据的局部结构，生成更清晰的样本，同时避免了传统 VAE 中后验分布和先验分布之间的 KL 散度优化带来的不稳定性。因此和传统的VAE差异在于将 "潜在空间"替换为离散的 码本（codebook）

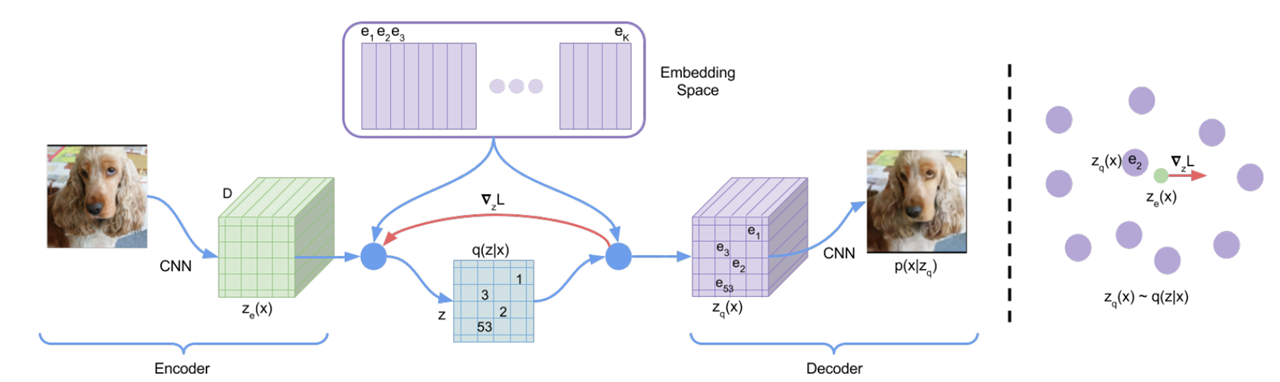
值得注意的：VQ-VAE不能直接用于生成新的样本，需要一个额外的先验模型去建模离散的潜在变量

这里不对数学原理做过多解释，直接解释代码如何操作，唯一的区别就是在于如何去构建 "离散化的码本"，对于输入图像通过编码器处理之后：
第一步 、生成我们的码本：\(C=[e+k]_{k=1}^K\) 代表K个嵌入向量以及每个向量维度为D。可以直接通过：nn.Embedding(num_embeddings, embedding_dim)
第二步 、直接将encoder处理后的内容"拉平"（\((B,C,H,W)\rightarrow (N,D)\) 其中 \(N=B\times H\times W\)）而后计算拉平后的内容和 码本之间的距离，并且返回距离最小的码本向量（\(K,D\)）索引：\(k=argmin_j \Vert z_e^i- e_j \Vert _2^2\)，而后将结果丢到one-hot矩阵（\((N,K)\)）中指导每个输入向量选择哪些码本向量
第三步 、将码本权重和one-hot相乘得到量化向量：\(z_q\in [N,D]\)
第四步 、计算损失：1、承诺损失（编码器输出和量化输出均方误差）；2、量化损失（量化输出和编码器输出的均方误差）；而后对两部分进行加权
第五步 、困惑度：监控码本利用率：\(exp(-\sum_k p_klogp_k)\)

说人话就是：编码后的向量会将这个向量映射到一个"字典"（也就是我们的码本，可以理解为这个码本存储了我们所有特征，最开始VAE是用连续分布做的）上，具体映射方法就是计算编码器的连续输出和码本中向量最接近的向量，然后用这个向量替换原始特征，但是这个码本开始是不行的，因此就需要计算损失来更新，因此就直接计算码本和编码器输出损失，于此同时也为了保证编码器输出和码本接近也计算损失，但是量化过程（选最近向量）没法直接算梯度，所以用"直通"方法：前向传播用码本选择的向量反向传播时假装梯度直接传回编码器输出。困惑度检查码本向量使用情况。如果困惑度低，说明有些向量没被用（"死码"），需要优化。

3.代码操作

说一千到一万不如直接看代码操作！代码上VAE代码比较简单主要是3个模块：1、encoder；2、decoder；3、潜在空间。在encoder/decoder中就都是通过一个神经网络构建而成的，没有太多需要解释的，不过需要注意的是在通过 encoder 直接处理之后，会额外通过神经网络去"拟合"：\(\mu\) 和 \(\sigma\) 去代表潜在空间的分布，除此之外在 潜在空间 处理上还会计算我们引入的随机变量 \(\epsilon\)，通过下面图像解释：

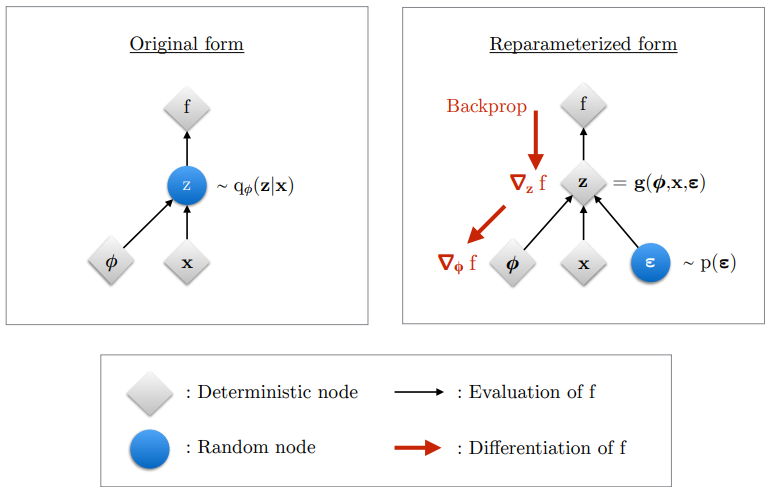
因此代码结构上（以MNIST数据集为例）：

python 复制代码 
class VAE(nn.Module):
    def __init__(self, latent_dim=20, input_dim=784):
        super(VAE, self).__init__()
        self.encoder = nn.Sequential(
            nn.Linear(input_dim, 256),
            nn.ReLU(),
            nn.Linear(256, 128),
            nn.ReLU()
        )
        self.fc_mu = nn.Linear(128, latent_dim)
        self.fc_var = nn.Linear(128, latent_dim)
        self.decoder = nn.Sequential(
            nn.Linear(latent_dim, 128),
            nn.ReLU(),
            nn.Linear(128, 256),
            nn.ReLU(),
            nn.Linear(256, input_dim),
            nn.Sigmoid()
        )

    def encode(self, x):
        h = self.encoder(x)
        return self.fc_mu(h), self.fc_var(h)

    def reparameterize(self, mu, logvar):
        std = torch.exp(0.5 * logvar)
        eps = torch.randn_like(std)
        return mu + eps * std

    def decode(self, z):
        return self.decoder(z)

    def forward(self, x):
        x = x.view(-1, VAE_CONFIG['image_size'])
        mu, logvar = self.encode(x)
        z = self.reparameterize(mu, logvar)
        recon_x = self.decode(z)
        return recon_x, mu, logvar

整体的代码结构很简单，在loss计算上，最开始我们的优化是：

\[L(\theta, \varphi,x)=E_{q_{\varphi}(\mathbf{Z}|\mathbf{X})}[\log p_{\theta}(\mathbf{x}|\mathbf{z})]-D_{KL}(q_{\varphi}(\mathbf{z}|\mathbf{x})\|p_{\theta}(\mathbf{z})) \]

其中第一项为我们的重建项（可以直接通过BCE loss来计算）、第二项为KL散度（存在解：\(D_{KL}=\frac{1}{2}\sum_{j=1}^{d}(\mu_j^2+\sigma_j^2-log\sigma_j^2-1)\)）。

python 复制代码 
def vae_loss(recon_x, x, mu, logvar):
    recon_x = torch.clamp(recon_x, 1e-8, 1-1e-8)
    x = x.view(-1, VAE_CONFIG['image_size'])
    BCE = nn.functional.binary_cross_entropy(recon_x, x, reduction='sum')
    KLD = -0.5 * torch.sum(1 + logvar - mu.pow(2) - logvar.exp())
    return (BCE + KLD) / x.size(0)  # 平均损失

所有的代码：1、VAE；2、PixelCNN

实际生成效果

VAE测试的主要是生成效果（MNIST数据集），而VA-VAE则是测试重构效果

VAE在MNIST数据集上表现

固定输入 重构图像 随机生成

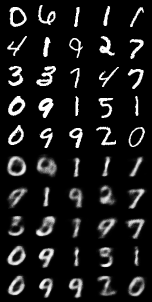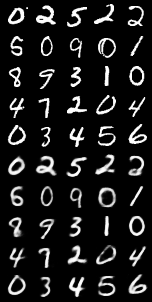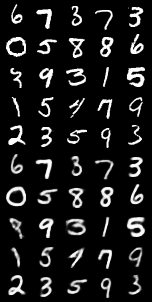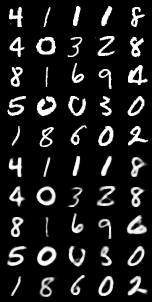不过值得注意的是 MNIST数据集很简单所以VAE可以很容易就生成需要的图片
VQ-VAE 在CIFAR10数据集上重构图像的表现（生成图像只是测试代码运行效果，CIFAR10数据集自身也比较复杂！，在CIFAR10上都没能生成较好的图片）

重构图像 PixelCNN生成图像 PixelCNNPlusPlus 生成图像 GatedPixelCNN 生成图像

总结

本文主要介绍了VAE的基本原理以及不同参数的求解，除此之外介绍了VQ-VAE的基本原理。两种差异在于：潜在用连续分布替换特征，后者用离散分布替换特征。对于VAE代码在模型上不难只需要在最后生成潜在空间过程中通过神经网络拟合 \(\mu\) 和 \(\sigma\)以及会额外的生成一个随机变量 \(\epsilon\)在损失函数计算中也只需要注意 \(D_{KL}\)和重建项的计算即可。

参考

1、https://github.com/hkproj/vae-from-scratch-notes/blob/main/VAE.pdf

2、https://mbernste.github.io/posts/vae/

3、https://arxiv.org/pdf/1906.02691

4、https://arxiv.org/pdf/1312.6114

5、https://arxiv.org/pdf/1711.00937

热门推荐
01KGG转MP3工具|非KGM文件|解密音频02YOLOv8入门 | 重要性能衡量指标、训练结果评价及分析及影响mAP的因素【发论文关注的指标】03从零安装 LLaMA-Factory 微调 Qwen 大模型成功及所有的坑04【SpeedAI科研小助手】2分钟极速解决知网维普重复率、AIGC率过高，一键全文降！文件格式不变，公式都保留的！05YOLOv5改进 | 添加CA注意力机制 + 增加预测层 + 更换损失函数之GIoU06Coze扣子平台完整体验和实践（附国内和国际版对比）07Ubuntu24.04安装中文输入法08DeepSeek各版本说明与优缺点分析09苍穹外卖面试总结10组基轨迹建模 GBTM的介绍与实现（Stata 或 R）