大家好,今天还是继续我们的动态规划里面的背包问题,前面我们主要接触的是0-1背包和完全背包,其实这两个背包问题主要就是看看每一件物品我们是否有多件,如果每一件物品我们只能取一次的话那这样我们就是0-1背包,如果每一件物品我们可以取多件的话那这样就是完全背包,那我们就接着以前的来继续我们今天的题目。
第一题对应力扣上编号为322的题目零钱兑换
这道题大家听到题目名字应该就会有种熟悉的感觉,我们是不是前面做过,是的我们前面的确做过一道关于零钱兑换的题目,而且我们在贪心算法章节还刷过一道叫做柠檬水找零的题目,那我们看看这道题目跟我们以前做过的有什么不一样的:

其实这道题目的背景与我们前面的那道零钱兑换的题目是一样的,不过那道题目让我们求的是可以凑出给定数额的组合方案数,而这一道题目让我们求的是凑出给定数额的所需的最少硬币个数,其实很明显题目还是很经典的完全背包问题,因为我们每种硬币的数量是无限的,但本题和纯完全背包不一样,**纯完全背包是凑成背包最大价值是多少,而本题是要求凑成总金额的物品最少个数!**那我们还是尝试使用完全背包问题来解决,还是动用动规五部曲。
首先动规五部曲的第一步就是确定dp数组的含义,其实这里的话我们使用一维dp数组就可以了,dp[j]:凑足总额为j所需钱币的最少个数为dp[j]。
第二步就是确定递推公式,我们需要仔细考虑一下,因为题目要求我们去求凑出给定金额的最少的钱币数,所以我们可以大致猜测肯定要出现取min值,我们很容易知道凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i],那如果不考虑coins[i]呢?那就是dp[j], 那这样两个取最小值不就是我们的递推公式了。
第三步就是初始化dp数组,我们首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;
这个是很明显的,考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。因为我们每一次都要取最小值,这样可以保证每次都可以正确更新所需的最少钱币数。
第四步就是确定遍历顺序,本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。那其实我们先遍历钱币再遍历金额是可以的,反过来也是可以的。
还有一步比较重要的就是举例推导dp数组,以代码随想录的例子为例:
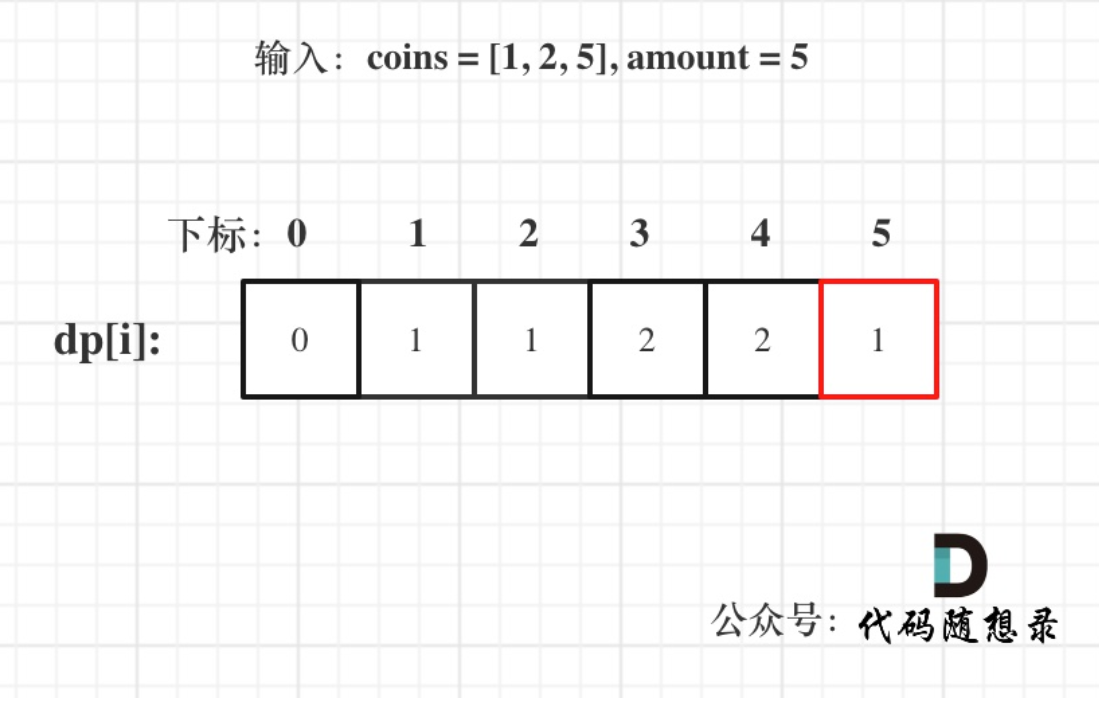
那我们可以尝试给出代码:
cpp
class Solution {
public:
int coinChange(vector<int>& coins, int amount) {
vector<int> dp(amount + 1, INT_MAX);
//初始化dp数组
dp[0] = 0;
//先遍历钱币再遍历总额
for (int i = 0; i < coins.size(); ++i)
{
for (int j = coins[i]; j <= amount; ++j)
{
//如果被更新了就说明存在最少的硬币数而且可以被凑出
if (dp[j - coins[i]] != INT_MAX)
{
dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
}
}
}
if (dp[amount] == INT_MAX) return -1;
return dp[amount];
}
};第二题对应力扣编号为279的题目完全平方数
这是我们今天的第二题,这道题我们以前没有见过比较类似的背景,我们就直接看看这道题目的要求:

读完题目之后我就知道了,其实就是凑出这个数我们至少需要几个完全平方数,这个题目似乎与上一道题目比较类似,其实都是填满背包至少需要多少件物品类型题目,很明显这个题目还是完全背包,那我们还是得用动规五部曲来解决。
第一步还是确定dp数组的含义,dp[j]:和为j的完全平方数的最少数量为dp[j]。
第二步就是递推公式,这道题目的递推公式与上一道题目的递推公式是异曲同工,还是我们考虑我是是否使用当前的完全平方数,当然我们不需要去写一个函数判断一个数是不是完全平方数,这里的每一个数就相当于我们上一道题的钱币金额,所以我们的递推公式大家或许就知道了应该是dp[j] = min(dp[j - i * i] + 1, dp[j])。
第三步一样的思路还是dp数组的初始化,dp[0] = 0其实这里可能有同学存在疑问,明明0*0 = 0那为啥dp[0] = 1不对呢,看题目描述,找到若干个完全平方数(比如 1, 4, 9, 16, ...),题目描述中可没说要从0开始,dp[0]=0完全是为了递推公式。所以其实这个dp[0] = 0没有什么意义,从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。这里其实与我们上面的题目也是类似的。
第四步就是确定遍历顺序,我们还是使用完全背包的思路,先遍历物品再遍历背包就可以了。
第五步就是打印验证dp数组这里就不说了,这个大家可以自行去测试。接下来走完动规五部曲以后我们就可以写出这道题目的解题代码:
cpp
class Solution {
public:
int numSquares(int n) {
vector<int> dp(n + 1, INT_MAX);
dp[0] = 0;
//遍历物品
for (int i = 1; i <= n; ++i)
{
//遍历背包其实也就是我当前使用完全平方数和凑出来的和
for (int j = i * i; j <= n; ++j)
{
//这是我们的递推公式,如果我想用一个i * i凑出的完全平方数就得先看前面那个数的需要
//完全平方数的个数然后加1就可以了
dp[j] = min(dp[j - i * i] + 1, dp[j]);
}
}
return dp[n];
}
};第三题对应力扣编号为139的题目单词拆分
这是我们今天的最后一道题目,我们动态规划章节似乎也没有遇到过背景相似的题目,所以我们就先看看题目的要求:

题目是给我们一个字符串列表里面存放了一些单词,给定我们一个字符串,看看这个字符串是否可以由我们字符串列表里面的单词拼接出来,而且字符串列表里面的单词都是可以重复使用的,很明显这还是一道完全背包的问题,那我们还是使用动规五部曲来解决这道题目。
第一步确定dp数组以及下标的含义:dp[i] : 字符串长度为i的话,dp[i]为true,表示可以拆分为一个或多个在字典中出现的单词。这题目有点特殊,所以我们定义的dp数组也是有点奇怪,第一次出现过bool类型的dp数组。
第二步就是我们的确定递推公式,这或许很奇怪,既然我们的dp数组都定义成了bool类型的那我们还有什么递推公式,其实是这样的:如果确定dp[j] 是true,且 [j, i] 这个区间的子串出现在字典里,那么dp[i]一定是true。(j < i )。这个听起来很抽象其实不难理解,我们dp[j]已经凑出了,只要我们[j,i]的区间里面存在我们长度为j与长度为i相差的字符串,那不就说明长度为i的字符串也可以被凑出了。这个思路很有趣,大家要好好积累一下。
第三步是dp数组如何初始化,从递推公式中可以看出,dp[i] 的状态依靠 dp[j]是否为true,那么dp[0]就是递推的根基,dp[0]一定要为true,否则递推下去后面都都是false了。大家可以想想其实题目也说了我们的字符串是非空的,其实dp[0]完全是为了递推公式服务。
第四步就是遍历顺序,这其实还是一道完全背包的题目,那我们其实还是可以按照完全背包的遍历顺序,其实单词就是物品,题目所给字符串就是背包,题目还是有需要注意的地方,这道题目是在意顺序,其实也就是排列问题而不是组合问题,如何理解?拿 s = "applepenapple", wordDict = ["apple", "pen"] 举例。"apple", "pen" 是物品,那么我们要求 物品的组合一定是 "apple" + "pen" + "apple" 才能组成 "applepenapple"。"apple" + "apple" + "pen" 或者 "pen" + "apple" + "apple" 是不可以的,那么我们就是强调物品之间顺序。所以我们就知道了这道题目我们就只能先遍历背包再遍历物品,如果我们先遍历物品再遍历背包就会出现乱序的情况,这点大家必须注意。
那这样其实题目的代码与以前似乎还是有些不一样:
cpp
class Solution {
public:
bool wordBreak(string s, vector<string>& wordDict) {
unordered_set<string> wordSet(wordDict.begin(), wordDict.end());
vector<bool> dp(s.size() + 1, false);
dp[0] = true;
for (int i = 1; i <= s.size(); i++) { // 遍历背包
for (int j = 0; j < i; j++) { // 遍历物品
string word = s.substr(j, i - j); //substr(起始位置,截取的个数)
if (wordSet.find(word) != wordSet.end() && dp[j]) {
dp[i] = true;
}
}
}
return dp[s.size()];
}
};今日总结
我们今天的题目其实有难度,大家得多多思考,理解动态规划并不容易,尤其是单词拆分这道题目的确很有难度,我们得理解为什么必须先遍历背包再遍历物品,以及我们要区分题目是考察的我们是组合问题还是排列问题,就是看看有没有顺序要求即可,这就是我们今天的讲解,我们明天见!