数学建模——递归和动态规划

1.问题引入

这个还得从实际问题出发

假设你在商店购物，最后需要用硬币支付，并且每次用的硬币数量要最少，并且总额不能超。而你现在有三种面额的硬币，分别是2，5，7

例如，假设你买了12块钱的东西.那么可能的方法有：

2+5+5，7+5，2*6，由于**硬币数量要最少，**因此7+5是最好的选择

那么怎么求出7+5这个答案呢，如果只有12块钱可能还好，但是假如现在有27块钱，那么可以选的方法就多了，直接枚举肯定行不通

2.递归

因此我们先从最后的答案出发

由于总额不能超27，又因为硬币只有三种面额，那除去最后一个硬币，之前所有硬币的价值就可以有三种情况（假设用了n枚硬币）

|---------------------|--------------------|---------------------|
| 25 +2 （n-1） | 22 +5（n-1） | 20 +7 （n-1） |

现在假设有一个函数可以算最小硬币数，x代表总面额,那么就有

那

现在我们关心的就不再是而是

同理假如现在要求同样带入

获得

以此类推，直到找到已知条件比如

这就有点像树的结构，每一条分支到0就结束如果是负数或者到1就无效

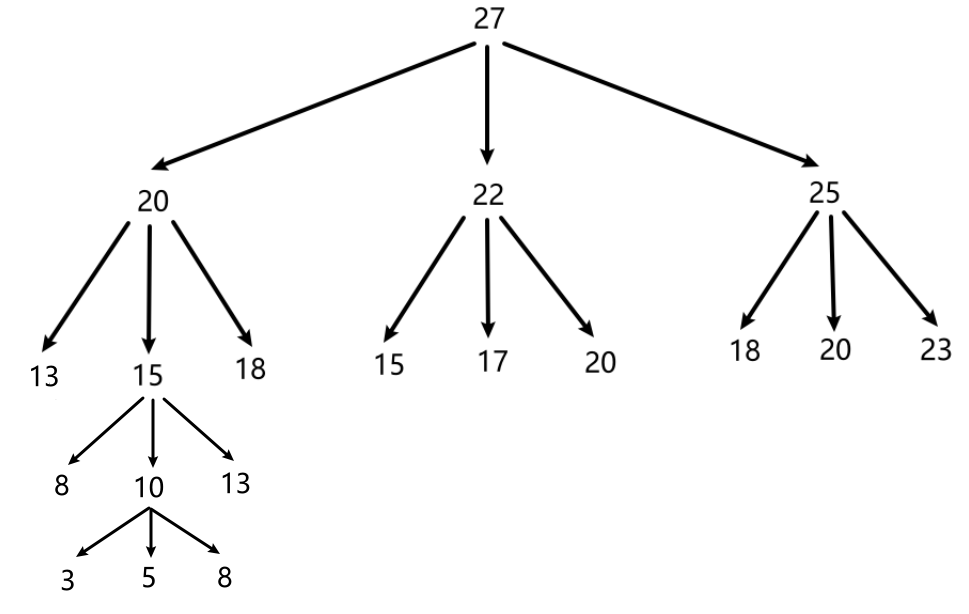
不难发现其实我们要的最少个数的方法，就是层数最少那一条分支

Matlab 复制代码

function res=f(x)
if x==0
else
    res=inf;
    if x>=2
        res=min(f(x-2)+1,res);
    end
    if x>=5
        res=min(f(x-5)+1,res);
    end
    if x>=7
        res=min(f(x-7)+1,res);
    end
end
end

这里有个比较巧妙的地方，一开始说的【每一条分支到0就结束如果是负数或者到1就无效】

在哪里处理的？

我们就能看出来递归其实就是先从结果往初始推，再推回结果的过程

递归：递就是****往初始推，归就是推回结果

虽然人看起来觉得代码简单，但是计算机要算的就多了

这里算27要知道20，22，25，算20要知道13，15，18，每增加一层就是3倍指数级的计算量增长

为啥多算了这么多，看第二行我们计算了20，22，25，看第三行我们又计算了20，甚至计算了两次，这下明白了，原来是重复计算的内容太多了，如果每次计算完一个数值存起来，那是不是后面就不用再算了，这样就简化了很多计算

3.动态规划

因此我们可以一开始就从初始向结果推导，把推导出的中间结果存起来便于后面使用，这种递推的方法就是动态规划

最开始有一个初始值

|---|-----------------------------------|---------------------------------|
| x | | |
| 值 | | |

同样的我们还是用这个公式

（状态转移方程）

然后一个一个计算并把结果存起来以便下次使用

|---|-----------------------------------|---------------------------------|-----|-----|-----|-----|-----|
| x | | | 1 | 2 | 3 | ... | 27 |
| 值 | | | inf | inf | inf | | inf |

|---|-----------------------------------|---------------------------------|-----|-----|-----|-----|-----|
| x | | | 1 | 2 | 3 | ... | 27 |
| 值 | | | inf | inf | inf | | inf |

|---|-----------------------------------|---------------------------------|-----|---|-----|-----|-----|
| x | | | 1 | 2 | 3 | ... | 27 |
| 值 | | | inf | 1 | inf | | inf |

|---|-----------------------------------|---------------------------------|-----|---|-----|-----|-----|
| x | | | 1 | 2 | 3 | ... | 27 |
| 值 | | | inf | 1 | inf | | inf |

|---|-----------------------------------|---------------------------------|-----|---|-----|---|-----|-----|
| x | | | 1 | 2 | 3 | 4 | ... | 27 |
| 值 | | | inf | 1 | inf | 2 | | inf |

|---|-----------------------------------|---------------------------------|---|-----|---|-----|----|
| x | | | 1 | 2 | 3 | ... | 27 |
| 值 | | | 1 | inf | 2 | | 5 |

vbscript 复制代码

function res=DP(n)
dp=Inf(1,n+1);
dp(1)=0;
for i=1:n
    if i>=2
        dp(i+1)=dp(i-2+1)+1;
    end
    if i>=5
        dp(i+1)=min(dp(i+1),dp(i-5+1)+1);
    end
    if i>=7
        dp(i+1)=min(dp(i+1),dp(i-7+1)+1);
    end
end
if dp(n+1)~=Inf
    res=dp(n+1);
else
    res=-1;
end
end

这里主要是避免出现负数所以分段写

4.补充(背包问题)

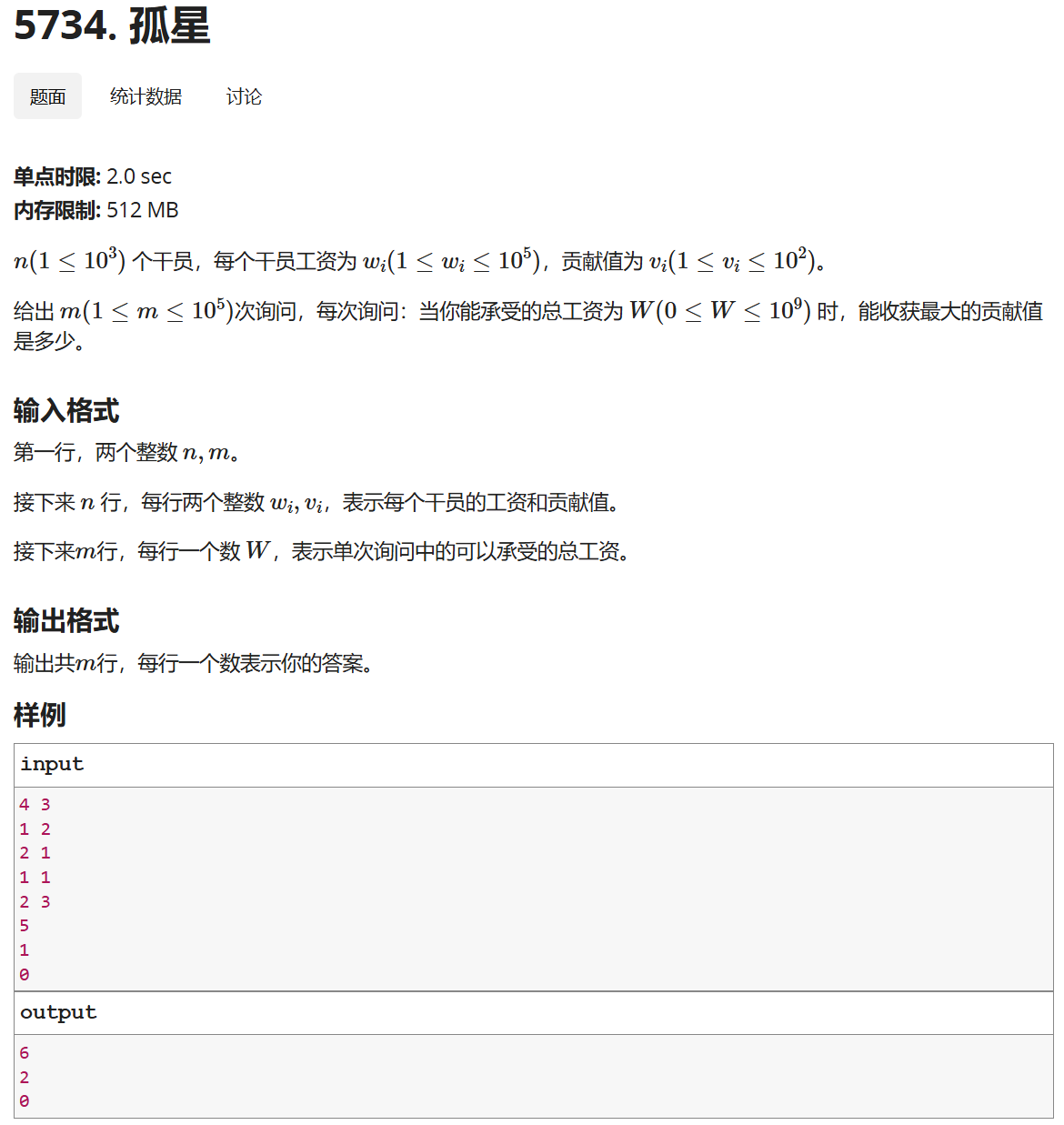
这个算是背包问题，背包问题的dp其实是二维的dp[i][j]->**dp[看到第i个物品为止][背包容量为j时]**物品的最大价值

同样的我们利用前面的思想

这里干员数组

|-----|---|---|---|---|
| 物品 | 1 | 2 | 3 | 4 |
| 工资 | 1 | 2 | 1 | 2 |
| 贡献值 | 2 | 1 | 1 | 3 |

dp初始数组

|-------------|---|---|---|---|---|---|---|
| 干员（贡献值）\工资 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1（2） | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2（1） | | | | | | | |
| 3（1） | | | | | | | |
| 4（3） | | | | | | | |

现在准备看第二个干员，当工资是0，或1时不需要考虑第二个干员，直接继承上面的数据，因为现在的工资不够第二个干员

当总工资是2时，显然不能同时放入两个干员，贡献值是意思是

要不就不要这个干员，现在总贡献值和只看了第一个干员的结果相同也就是=2

要不就要第二个干员，但是给其他干员预留的工资只有总资金-这个干员的工资=2-2=0

那么最高贡献值就是当工资0且只看该干员前面所有干员时的最高贡献值加上这个干员的贡献值，那招入第二个干员总贡献值最高就是

显然最大贡献值是2

|-------------|---|---|---|---|---|---|---|
| 干员（贡献值）\工资 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1（2） | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2（1） | 0 | 2 | 2 | | | | |
| 3（1） | | | | | | | |
| 4（3） | | | | | | | |

当总工资是3时

|-------------|---|---|---|---|---|---|---|
| 干员（贡献值）\工资 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1（2） | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2（1） | 0 | 2 | 2 | 3 | 3 | 3 | 3 |
| 3（1） | | | | | | | |
| 4（3） | | | | | | | |

现在准备看第三个干员，当工资是0时不需要考虑第三个干员，直接继承上面的数据，因为现在的工资不够第三个干员

|-------------|---|---|---|---|---|---|---|
| 干员（贡献值）\工资 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1（2） | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2（1） | 0 | 2 | 2 | 3 | 3 | 3 | 3 |
| 3（1） | 0 | | | | | | |
| 4（3） | | | | | | | |

当工资是1时，最大贡献值是

|-------------|---|---|---|---|---|---|---|
| 干员（贡献值）\工资 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1（2） | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2（1） | 0 | 2 | 2 | 3 | 3 | 3 | 3 |
| 3（1） | 0 | 2 | | | | | |
| 4（3） | | | | | | | |

当工资是2时，最大贡献值是

|-------------|---|---|---|---|---|---|---|
| 干员（贡献值）\工资 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1（2） | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2（1） | 0 | 2 | 2 | 3 | 3 | 3 | 3 |
| 3（1） | 0 | 2 | 3 | | | | |
| 4（3） | | | | | | | |

当工资是3时，最大贡献值是

|-------------|---|---|---|---|---|---|---|
| 干员（贡献值）\工资 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1（2） | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2（1） | 0 | 2 | 2 | 3 | 3 | 3 | 3 |
| 3（1） | 0 | 2 | 3 | 3 | | | |
| 4（3） | | | | | | | |

当工资是4时，最大贡献值是

|-------------|---|---|---|---|---|---|---|
| 干员（贡献值）\工资 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1（2） | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2（1） | 0 | 2 | 2 | 3 | 3 | 3 | 3 |
| 3（1） | 0 | 2 | 3 | 3 | 4 | 4 | 4 |
| 4（3） | | | | | | | |

最后看第四个干员，同样的容量0，1继承

|-------------|---|---|---|---|---|---|---|
| 干员（贡献值）\工资 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1（2） | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2（1） | 0 | 2 | 2 | 3 | 3 | 3 | 3 |
| 3（1） | 0 | 2 | 3 | 3 | 4 | 4 | 4 |
| 4（3） | 0 | 2 | | | | | |

当工资是2时，最大贡献值是

|-------------|---|---|---|---|---|---|---|
| 干员（贡献值）\工资 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1（2） | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2（1） | 0 | 2 | 2 | 3 | 3 | 3 | 3 |
| 3（1） | 0 | 2 | 3 | 3 | 4 | 4 | 4 |
| 4（3） | 0 | 2 | 3 | | | | |

当工资是3时，最大贡献值是

|-------------|---|---|---|---|---|---|---|
| 干员（贡献值）\工资 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1（2） | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2（1） | 0 | 2 | 2 | 3 | 3 | 3 | 3 |
| 3（1） | 0 | 2 | 3 | 3 | 4 | 4 | 4 |
| 4（3） | 0 | 2 | 3 | 5 | | | |

当工资是4时，最大贡献值是

|-------------|---|---|---|---|---|---|---|
| 干员（贡献值）\工资 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1（2） | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2（1） | 0 | 2 | 2 | 3 | 3 | 3 | 3 |
| 3（1） | 0 | 2 | 3 | 3 | 4 | 4 | 4 |
| 4（3） | 0 | 2 | 3 | 5 | 6 | | |

当工资是5时，最大贡献值是

|-------------|---|---|---|---|---|---|---|
| 干员（贡献值）\工资 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 1（2） | 0 | 2 | 2 | 2 | 2 | 2 | 2 |
| 2（1） | 0 | 2 | 2 | 3 | 3 | 3 | 3 |
| 3（1） | 0 | 2 | 3 | 3 | 4 | 4 | 4 |
| 4（3） | 0 | 2 | 3 | 5 | 6 | 6 | 7 |

当工资是6时，最大贡献值是

看结果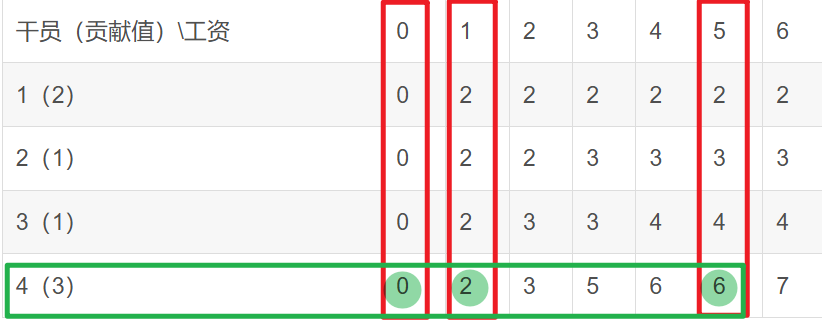

这下面是我拿c语言瞎写的代码，

cpp 复制代码

#include<stdio.h>
int main() {
	int m, n;
	scanf("%d %d", &m, &n);
	int  ganyuan[100][100];
	int q[100];
	for (int i = 0; i < m; i++)
	{
		scanf("%d %d", &ganyuan[1+i][0],&ganyuan[1+i][1]);
	}
	for (int i = 0; i < n; i++)
	{
		scanf("%d", &q[i]);
	}
	int dp[100][100];
	for (int i = 0; i < 10; i++)
	{
		dp[0][i] = 0;
	}
	for (int i = 1; i <= m; i++)
	{
		for (int j = 0; j < 10; j++)
		{
			if (ganyuan[i][0] > j) {
				dp[i][j] = dp[i - 1][j];
			}
			else 
			{
				if (dp[i-1][j- ganyuan[i][0]]+ ganyuan[i][1] > dp[i - 1][j])
				{
					dp[i][j] = dp[i - 1][j - ganyuan[i][0]] + ganyuan[i][1];
				}
				else
				{
					dp[i][j] = dp[i - 1][j];
				}
			}
		}
	}
	for (int i = 0; i < n; i++)
	{
		printf("%d ", dp[m][q[i]]);
	}
	/*for (int i = 1; i <= m; i++)
	{
		for (int j = 0; j < 10; j++)
		{
			printf("%d ", dp[i][j]);
		}
		printf("\n");
	}*/
	return 0;
}

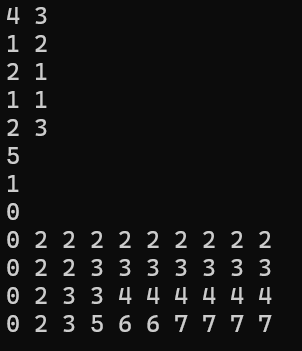勉强能跑，但是只能解决小数据的问题，如果像题目这种数据特别大，还得用其他方法优化