在数据处理的世界里,我们常常会遇到这样的问题:数据量太大,存储和传输成本高昂,但又不能丢失重要信息。
这时候,压缩感知 (Compressive Sensing,CS)就像一位神奇的"数据魔法师",能够帮助我们高效地处理数据。
本文我们就来深入了解一下压缩感知是什么,它的原理和作用,以及如何用代码实现它。
1. 压缩感知是什么?
压缩感知 是一种新兴的信号处理技术,它打破了传统信号处理中**"先采样再压缩"**的模式。
在传统的信号处理中,我们通常需要按照奈奎斯特采样定理 (Nyquist Sampling Theorem)来采集信号,即采样频率至少是信号最高频率的两倍。
这样做的结果就是会产生大量的数据,其中很多数据可能是冗余的。
而压缩感知 的核心思想是:信号在某些域(如小波域)中往往是稀疏的,也就是说大部分的系数是零或者接近零的。
我们可以利用这种稀疏性,在采样的同时进行压缩,直接获取信号的少量关键信息,然后通过特定的算法重建出原始信号。
2. 压缩感知主要原理
压缩感知的实现原理主要基于下面三个方面:
2.1. 信号的稀疏性
信号的稀疏性 是压缩感知的基础。
假设我们有一个信号\(x\) ,它在某个变换域(如小波变换、傅里叶变换等)中表示为 \(\theta x\) ,
其中\(\theta\) 是变换矩阵。如果 \\theta x 中大部分元素是零或者接近零,那么我们称信号 x 在该域是稀疏的。
例如,一个音频信号在小波域中可能只有少数几个小波系数是显著的,其他大部分系数都是零。
2.2. 测量矩阵
为了获取信号的关键信息,我们需要设计一个测量矩阵 \\Phi 。
这个矩阵的作用是将原始信号 x 投影到一个低维空间,得到测量值 y 。
测量值的数量 m 通常远小于原始信号的维度 n ,即 m\\ll n 。
测量过程可以用公式表示为: y=\\Phi x
其中, y 是测量值, \\Phi 是测量矩阵, x 是原始信号。
2.3. 信号重建
有了测量值 y 测量矩阵 \\Phi ,我们还需要通过某种算法重建出原始信号 x 。
由于 m\\ll n ,这是一个欠定方程组,有无数个解。
但因为信号是稀疏的,我们可以通过求解以下优化问题来找到最稀疏的解:
\\min\|x\|_1\\quad\\text{subject to}\\quad y=\\Phi x
这里, \|x\|_1 表示 x 的 L_1 范数,即 x 中所有元素绝对值的和。
通过最小化 L_1 范数,我们可以找到最稀疏的解。
3. 压缩感知的作用
压缩感知 的主要作用是高效地采集 和重建信号,它在许多领域都有广泛的应用,例如:
- 图像处理:在图像压缩和重建中,压缩感知可以减少存储和传输的数据量,同时保持图像的高质量。
- 无线通信:在无线传感器网络中,压缩感知可以减少传感器节点的能耗,延长网络的使用寿命。
- 生物医学成像 :在磁共振成像(
MRI)中,压缩感知可以减少扫描时间,提高成像效率。 - 雷达系统:提升目标识别速度。
压缩感知 与传统采样的对比如下表:
| 指标 | 传统采样 | 压缩感知 |
|---|---|---|
| 采样率需求 | 高 | 极低 |
| 硬件成本 | 高 | 低 |
| 重建复杂度 | 低 | 高 |
| 适用场景 | 常规信号 | 稀疏信号 |
4. 代码示例
接下来,我们用scikit-learn库来实现一个简单的压缩感知示例。
我们首先生成一个稀疏信号,通过测量矩阵获取测量值,然后用Lasso回归(一种基于 L_1 范数的优化算法)来重建信号。
python
import numpy as np
import matplotlib.pyplot as plt
from sklearn.linear_model import Lasso
# 1. 生成稀疏信号
n = 100 # 信号长度
k = 10 # 稀疏度
x_true = np.zeros(n)
x_true[:k] = np.random.randn(k) # 前 k 个元素是随机值,其余为零
np.random.shuffle(x_true) # 打乱顺序
# 2. 生成测量矩阵
m = 30 # 测量值数量
Phi = np.random.randn(m, n) / np.sqrt(m) # 随机高斯矩阵
# 3. 获取测量值
y = Phi @ x_true
# 4. 使用 Lasso 回归重建信号
lasso = Lasso(alpha=0.01, max_iter=10000)
lasso.fit(Phi, y)
x_reconstructed = lasso.coef_
print(len(y))
# 5. 绘制结果
plt.figure(figsize=(12, 6))
plt.subplot(2, 1, 1)
plt.stem(x_true, linefmt='b-', markerfmt='bo', basefmt='r-')
plt.title("原始稀疏信号")
plt.subplot(2, 1, 2)
plt.stem(x_reconstructed, linefmt='r-', markerfmt='ro', basefmt='r-')
plt.title("根据压缩信息重建的信号")
plt.show()代码中的5个步骤说明:
- 生成稀疏信号:我们创建了一个长度为 100 的信号,其中只有 10 个非零元素。这些非零元素是随机生成的,并且打乱了顺序。
- 生成测量矩阵:我们使用了一个随机高斯矩阵作为测量矩阵,其维度为 30\\times 100 。
- 获取测量值:通过矩阵乘法 y=\\Phi x 获取测量值。
- 重建信号 :使用
Lasso回归来重建信号。Lasso回归通过最小化 L_1 范数来找到最稀疏的解。 - 绘制结果:最后,我们绘制原始信号和重建信号的对比图。
运行结果如下:
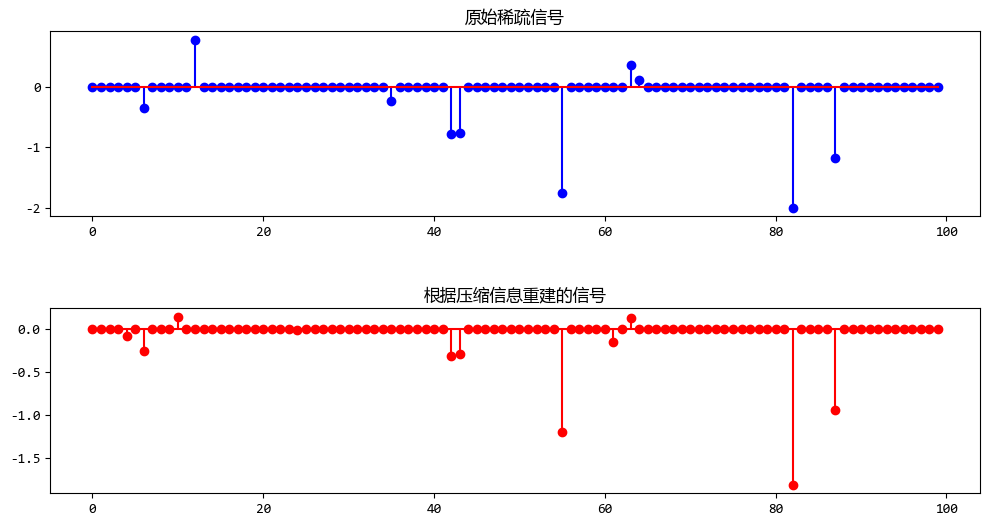
注意:因为数据是随机生成的,所以你执行的结果也许和上图不一样。
5. 总结
压缩感知是一种强大的信号处理技术,它利用信号的稀疏性,在采样的同时进行压缩,并通过优化算法重建信号。
在实际应用中,压缩感知可以大大提高数据处理的效率,减少存储和传输成本,同时保持信号的质量。