「ABC 406 G」Travelling Salesman Problem

前言

本题笔者使用了两种方法来做，一是 \(\text{Slope trick}\) ，二是线段树，皆有讲解，各位读者按需食用。

准备工作

对于该题，我们首先会有一个 \(O(NV^2)\) 的暴力 \(\text{dp}\) 。

令 \(dp_{i, j}\) 表示干掉前 \(i\) 个商人后人在位置 \(j\) 的最小代价，易得：

\[dp_{i, j} = min_{k = -V}^{V} \{ dp_{i - 1, k} + |j - k| \times c \} + |x_i - j| \times d \]

初始状态 \(dp_{0, i} = |i| \times c\)

显然，该 \(\text{dp}\) 可以用李超线段树一类来优化掉一个 \(V\) ，但这远远不够，所以我们思考转换模型。

首先对于 \(\text{dp}\) 的第一维 \(i\) 砍掉（层对层转移），然后我们将 \(dp_j\) 视为一个函数 \(f(i) = dp_i\) (此处 \(i\) 为前文 \(j\)) ，然后把图像画出来，可以发现是一个下凸包分段一次函数，可以通过数学归纳法证明。

首先，最初的函数是一个绝对值函数，为下凸包分段一次函数。

我们假设第 \(p\) 次转移后 \(f\) 仍是一个下凸包分段一次函数。对于 \(f(i)\) 我们进行分类讨论。

\(f(i + 1) - f(i) < -c\) ，则 \(f(i + 1) + c < f(i)\) ，所以对于所有 \(j\) 使得 \(j \leq i\) 都有从 \(i + 1\) 转移到 \(j\) 更优，以此推得对于位置 \(i\) 使得 \(f(i) - f(i - 1) < -c\) ，\(f(i + 1) - f(i) >= -c\) ，\(i\) 是所有 \(j \leq i\) 的最有决策点。在图像上形如将所有斜率小于 \(-c\) 削成 \(-c\)
\(f(i + 1) - f(i) > c\) ，即图像斜率 \(> 0\) 的部分，同上，于是有在图像上将所有斜率大于 \(c\) 的削成 \(c\) 。
\(f(i + 1) - f(i) > -c\) ，则 \(f(i + 1) + c > f(i)\) ，所以对于所有 \(j > i\) 我们从 \(j\) 转移到 \(i\) 一定不优
\(f(i - 1) - f(i) > -c\) ，则 \(f(i - 1) + c > f(i)\) ，所以对于所有 \(j < i\) 我们从 \(j\) 转移到 \(i\) 一定不优。
\(f(i + 1) - f(i) < c\) ，则 \(f(i + 1) > f(i)\) ，不优。
\(f(i - 1) - f(i) < c\) ，则 \(f(i - 1) > f(i)\) ，不优

综上，我们说明了什么呢，具象化即对于图像中所有斜率绝对值大于 \(c\) 的将其绝对值削成 \(c\) （不改变正负），对于所有斜率绝对值小于 \(c\) 的保持不变。所以对于第一步转移中我们有转移后仍是一个下凸包分段一次函数且对于 \(dp_i\) ，它的转移点为

\(opt_{i + 1}\) ，如果 \(dp_{i + 1} - dp_i < -c\)
\(opt_{i - 1}\) ，如果 \(dp_i - dp_{i - 1} > c\)
\(i\)

借此，我们就可以将第 \(i\) 次转移（与 \(dp\) 下标 \(i\) 不同）后函数斜率绝对值小于 \(c\) 的部分的左端点 \(l_i\) 和右端点 \(r_i\) 记录下来，最后我们对于最终的最优决策点 \(p\) 只需对于 \(i\) 倒着从 \(n\) 到 \(2\) 按 \(p \leftarrow max(l_i, min(r_i, p))\) 取一遍就可以得到方案序列。

现在回档，对于第二步修改形如在原函数上加一个下凸绝对值函数，也是一个下凸分段一次函数。因为对于两个同为下凸或同为上凸的分段一次函数相加（卷积下确界）仍是一个下凸或上凸分段一次函数（原因详见OI WIKI），所以在第二部修改后仍是一个下凸分段一次函数，这就证明完了。

现在来谈谈维护这个函数的整个流程。

首先，我们对于该函数在一次转移中的大致流程是这样的：

假设 \(c = 5\) , \(d = 2\) ，\(a_i = 0\)

转移前:

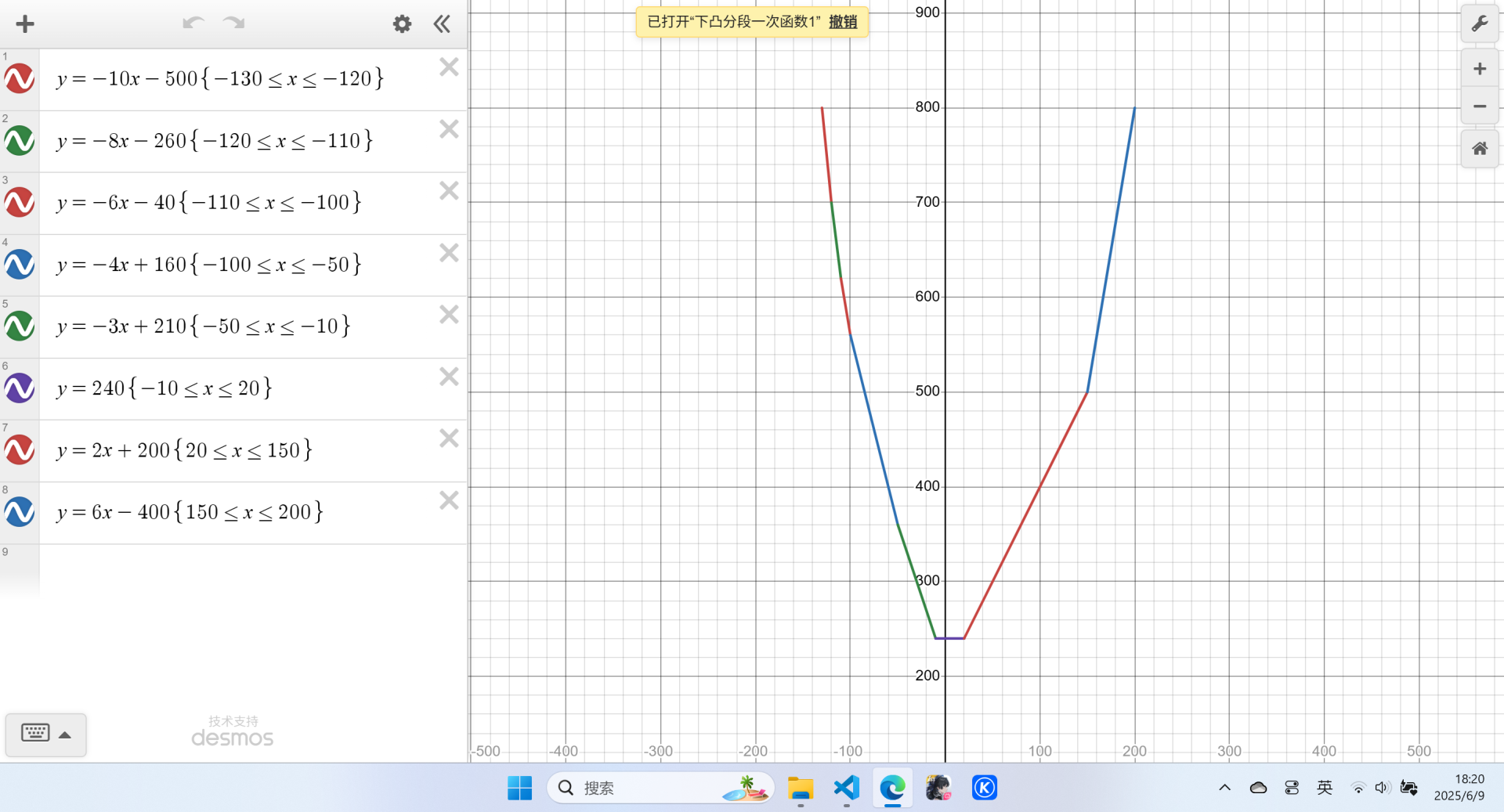
第一步转移后：

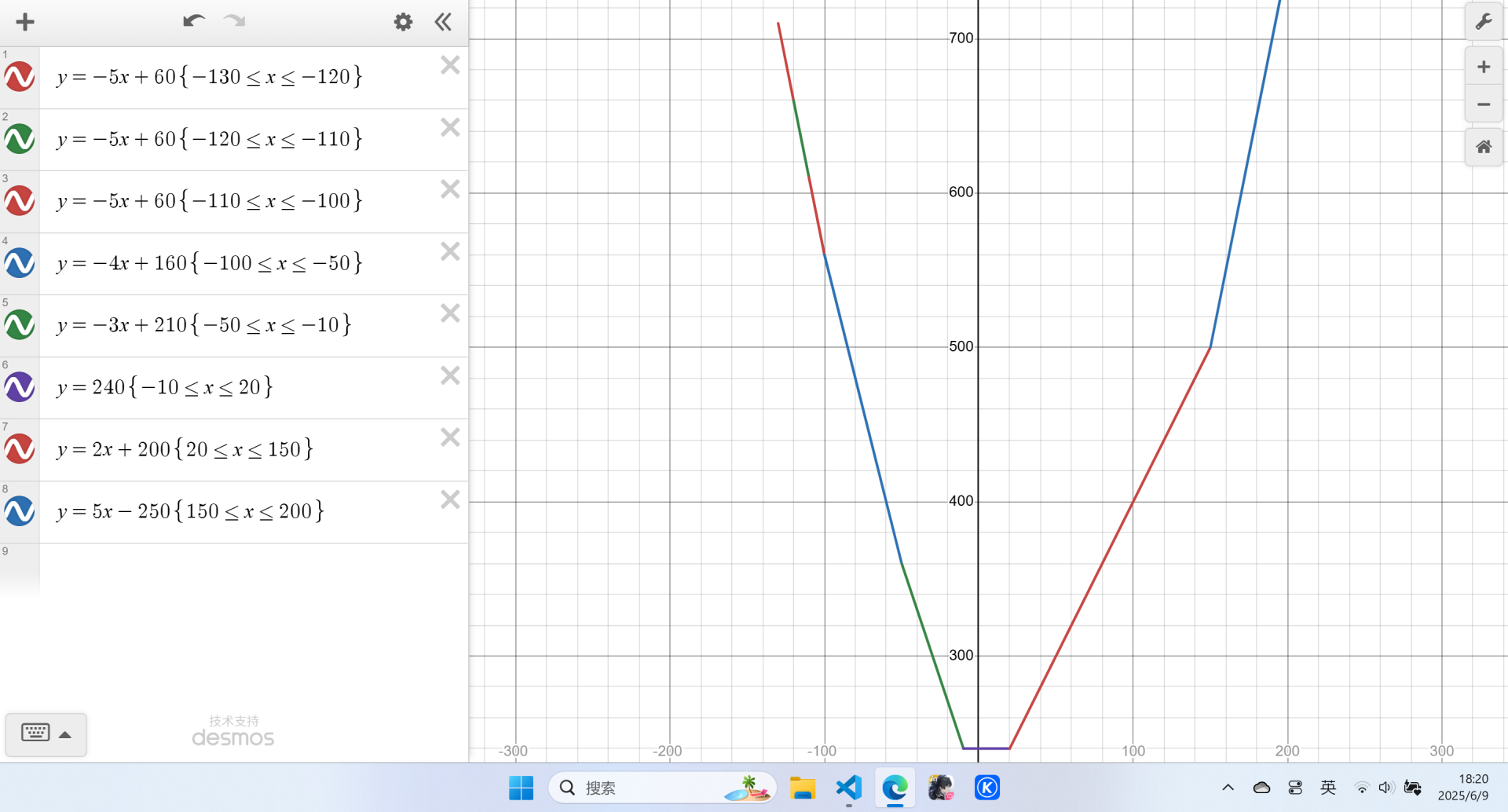
第二步修改后：

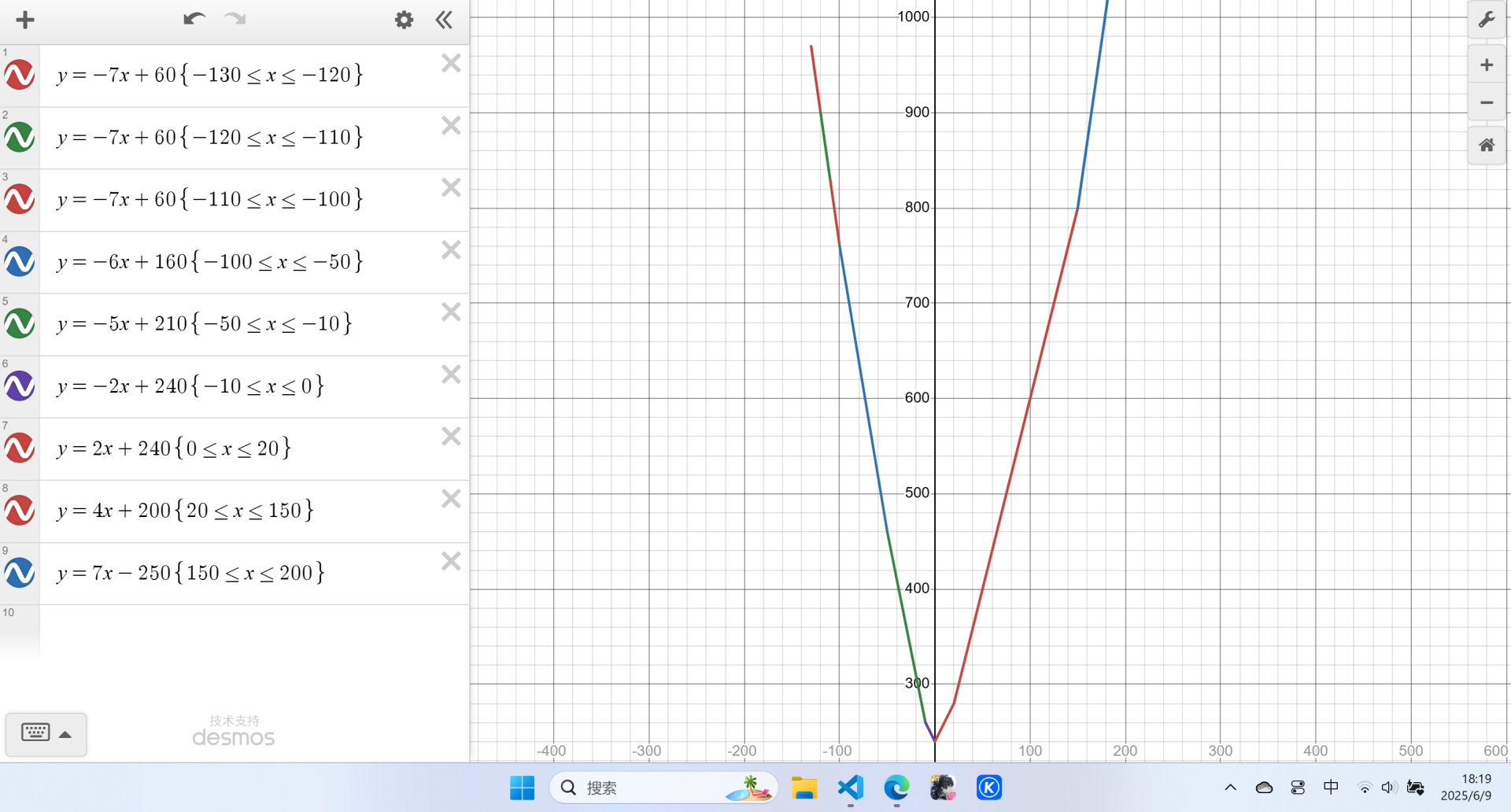
清楚了整个 \(\text{dp}\) 函数变化以及我们需求的信息后，就可以来着手维护了。

Slope trick

不熟悉 \(\text{Slope trick}\) 的可以先看看这篇、这篇或这篇文章。

对于我们需要维护的函数，我们发现其斜率变化量达到了 \(10^{10}\) 的量级，但值域只有 \(10^5\) 的量级，所以我们可以考虑把传统优先队列维护的方法改为用 \(\text{map}\) 维护，\(mp_i\) 表示在位置 \(i\) 斜率变化了 \(mp_i\) （不嫌麻烦可以写链表，可以砍掉一个 \(\log_2^V\) 。

对于平整两端的操作我们直接从 \(L\) 和 \(R\) 的begin和end往中间累加、判断并删除或修改即可，并记录下最后一次操作的位置，赋值给 \(l_i\) ，\(r_i\) 。

对于加入绝对值函数的操作我们按正常 \(\text{Slope trick}\) 的流程来就行，但这样有个问题，我们的 \(c\) 可能很小，然后 \(d\) 可能很大，导致加绝对值函数前的函数图像的斜率很小，在将 \(L\) 中的点移到 \(R\) 中时对于最后一个点会反复移动然后更新斜率又加了一个点到 \(L\) 中，共计 \(\left \lceil \frac{D}{C} \right \rceil\) 个点，成功

怎么解决呢？我们只需 \(min(2c, d) \rightarrow d\) 或在程序开头特判 \(d > 2c\)即可，我们发现对于 \(d > 2c\) 的情况我们让商人走是一定不优的，那么我们可以直接让玩家自己走路干掉所有商人，没必要让商人上门，所以可以在开始特判。嫌麻烦只需将 \(d\) 改成 \(2c\) 即可（不影响抉择和答案）。

附上代码（注释是调试，读者有需要自行食用，借鉴的这篇题解）

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef unsigned long long ULL;
typedef long double ld;
typedef pair<int, int> pii;
typedef pair<int, LL> pil;
typedef pair<LL, int> pli;
typedef pair<LL, LL> pll;
typedef pair<int, bool> pib;
typedef pair<ld, int> pdi;
#define mkp make_pair
#define lowbit(x) (x & -x)
const int N = 5e5 + 5;
int l[N], r[N];
map<int, int>L, R;
int ksumL, ksumR;
LL ans;
int n, c, d, kadd;
int main() {
    scanf("%d%d%d", &n, &c, &d);
    kadd = min(c << 1, d);
    L[0] = R[0] = ksumL = ksumR = c;
    for (int i = 1;i <= n;++i) {
        int x;scanf("%d", &x);
        // printf("%d:\n", i);
        // printf("%d %d\n", int(L.size()), int(R.size()));
        // printf("%d %d\n", ksumL, ksumR);
        // puts("---------");
        // for (auto li : L) printf("%d -%d\n", li.first, li.second);
        // for (auto li : R) printf("%d %d\n", li.first, li.second);
        // puts("---------");
        while (c < ksumL)
            if (ksumL - L.begin()->second >= c) {
                ksumL -= L.begin()->second;
                L.erase(L.begin());
            }
            else {
                L.begin()->second -= ksumL - c;
                ksumL = c;
            }
        while (c < ksumR)
            if (ksumR - (--R.end())->second >= c) {
                ksumR -= (--R.end())->second;
                R.erase(--R.end());
            }
            else {
                (--R.end())->second -= ksumR - c;
                ksumR = c;
            }
        ksumL += kadd;ksumR += kadd;
        // printf("%d %d\n", int(L.size()), int(R.size()));
        l[i] = L.begin()->first;r[i] = (--R.end())->first;
        if (R.begin()->first >= x) L[x] += kadd;
        else
            while (kadd)
                if (R.begin()->second > kadd) {
                    ans += LL(max(0, x - R.begin()->first)) * kadd;
                    L[R.begin()->first] += kadd;
                    R.begin()->second -= kadd;
                    R[x] += kadd;
                    break;
                }
                else {
                    ans += LL(max(0, x - R.begin()->first)) * R.begin()->second;
                    kadd -= R.begin()->second;
                    L[R.begin()->first] += R.begin()->second;
                    int num = R.begin()->second;
                    R.erase(R.begin());
                    R[x] += num;
                }
        kadd = min(c << 1, d);
        if ((--L.end())->first <= x) R[x] += kadd;
        else
            while (kadd)
                if ((--L.end())->second > kadd) {
                    ans += LL(max(0, (--L.end())->first - x)) * kadd;
                    R[(--L.end())->first] += kadd;
                    (--L.end())->second -= kadd;
                    L[x] += kadd;
                    break;
                }
                else {
                    ans += LL(max(0, (--L.end())->first - x)) * (--L.end())->second;
                    kadd -= (--L.end())->second;
                    R[(--L.end())->first] += (--L.end())->second;
                    int num = (--L.end())->second;
                    L.erase(--L.end());
                    L[x] += num;
                }
        // puts("after change");
        // for (auto li : L) printf("%d -%d\n", li.first, li.second);
        // for (auto li : R) printf("%d %d\n", li.first, li.second);
        // puts("||||||||||||||||||||");
        kadd = min(c << 1, d);
    }
    // for (int i = 1;i <= n;++i) printf("%d %d\n", l[i], r[i]);
    vector<int>pos;
    pos.push_back(R.begin()->first);
    for (int i = n;i > 1;--i) {
        int lst = pos.back();
        if (lst > r[i]) lst = r[i];
        if (lst < l[i]) lst = l[i];
        pos.push_back(lst);
    }
    printf("%lld\n", ans);
    for (int i = n - 1;i >= 0;--i) printf("%d ", pos[i]);
    return 0;
}

线段树

对于函数操作，值域较小，操作有区间加等差数列，区间赋值等差数列，单点改斜率，查询斜率，查询值，发现这些操作即区间加等差数列，区间赋值，单点修改，都是线段树可以做的。区间 \([l, r]\) 打三个懒标记 \(tag, k, d\) 分别表示赋值、等差数列起始值、等差数列公差，无需额外变量（单点查询）。下传懒标记时注意左右儿子 \(k\) 不一样以及下传顺序即可。

对于斜率削平我们可以二分找到分割点，并通过区间赋值 \(+\) 区间加等差数列完成，加绝对值函数也用加等差数列，就是涉及一点简单计算。最后的答案可以扫一遍取最大值，脑抽了也可以像我一样写一个三分，都无所谓。

线段树没什么好讲的，主要就是实现细节的问题（注释同样自行食用调试，纯手打，无借鉴）。

cpp 复制代码

#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
const int N = 2e5 + 5;
const int V = 1e5;
struct SegmentTree {
#define ls (id << 1)
#define rs (id << 1 | 1)
#define mid (l + r >> 1)
    struct Segment {
        LL k, d, tag;
    }seg[N << 2];
    inline void build(int id, int l, int r) {
        seg[id].tag = -1;
        seg[id].k = seg[id].d = 0;
        if (l == r) return;
        build(ls, l, mid);build(rs, mid + 1, r);
    }
    inline void pushdown(int id, int l, int r) {
        if (seg[id].tag != -1) {
            // printf("Cover [%d, %d] %lld\n", l, r, seg[id].tag);
            seg[ls].tag = seg[rs].tag = seg[id].tag;
            seg[ls].k = seg[rs].k = seg[ls].d = seg[rs].d = 0;
            seg[id].tag = -1;
        }
        if (seg[id].d || seg[id].k) {
            seg[ls].d += seg[id].d;
            seg[rs].d += seg[id].d;
            seg[ls].k += seg[id].k;
            seg[rs].k += seg[id].k + seg[id].d * (mid - l + 1);
            // printf("[%d, %d] %lld %lld -> [%d, %d] %lld %lld and [%d, %d] %lld %lld\n", l, r, seg[id].k, seg[id].d, l, mid, seg[ls].k, seg[ls].d, mid + 1, r, seg[rs].k, seg[rs].d);
            seg[id].d = seg[id].k = 0;
        }
    }
    inline void modify(int id, int l, int r, int L, int R, LL k, LL d) {
        // printf("%d %d %lld %lld\n", l, r, k, d);
        if (l >= L && R >= r) {
            seg[id].k += k;
            seg[id].d += d;
            // printf("[%d, %d] add %lld %lld result %lld %lld\n", l, r, k, d, seg[id].k, seg[id].d);
            return;
        }
        pushdown(id, l, r);
        if (L <= mid) modify(ls, l, mid, L, min(mid, R), k, d);
        if (R > mid) modify(rs, mid + 1, r, max(mid + 1, L), R, k + max((mid - L + 1), 0) * d, d);
    }
    inline void update_delta(int id, int l, int r, int x, LL d) {
        if (l == r) return seg[id].d = d, void(0);
        pushdown(id, l, r);
        if (x <= mid) update_delta(ls, l, mid, x, d);
        else update_delta(rs, mid + 1, r, x, d);
    }
    inline void cover(int id, int l, int r, int L, int R, LL c) {
        if (l >= L && R >= r) {
            seg[id].d = 0;
            seg[id].k = seg[id].tag = c;
            return;
        }
        pushdown(id, l, r);
        if (L <= mid) cover(ls, l, mid, L, R, c);
        if (R > mid) cover(rs, mid + 1, r, L, R, c);
    }
    inline LL ask(int id, int l, int r, int x) {
        // printf("[%d, %d]:%lld %lld\n", l, r, seg[id].k, seg[id].d);
        if (l == r) return seg[id].k;
        pushdown(id, l, r);
        if (x <= mid) return ask(ls, l, mid, x);
        else return ask(rs, mid + 1, r, x);
    }
    inline LL delta(int id, int l, int r, int x) {
        if (l == r) return seg[id].d;
        pushdown(id, l, r);
        if (x <= mid) return delta(ls, l, mid, x);
        else return delta(rs, mid + 1, r, x);
    }
}SGT;
int l[N], r[N];
int n;
LL c, d;
inline int find() {
    int l = -V, r = V, ret = V;
    while (l <= r) {
        int mid1 = l + (r - l + 1) / 3, mid2 = l + (r - l + 1) * 2 / 3;
        if (SGT.ask(1, -V, V, mid1) < SGT.ask(1, -V, V, mid2)) ret = mid1, r = mid2 - 1;
        else ret = mid2, l = mid1 + 1;
    }
    return ret;
}
inline int Less() {
    int l = -V, r = V, ret = -V - 1;
    while (l <= r)
        // printf("delta %d %d\n", mid, SGT.delta(1, -V, V, mid));
        if (SGT.delta(1, -V, V, mid) <= -c) ret = mid, l = mid + 1;
        else r = mid - 1;
    // printf("%d\n", ret);
    return ret;
}
inline int Greater() {
    int l = -V, r = V, ret = V;
    while (l <= r)
        if (SGT.delta(1, -V, V, mid) >= c) ret = mid, r = mid - 1;
        else l = mid + 1;
    return ret + 1;
}
int main() {
    scanf("%d%lld%lld", &n, &c, &d);
    SGT.build(1, -V, V);
    SGT.modify(1, -V, V, -V, -1, V * c, -c);
    SGT.modify(1, -V, V, 0, V, 0, c);
    // SGT.ask(1, -V, V, -114);
    // puts("--------------");
    // SGT.ask(1, -V, V, 114);
    // puts("--------------");
    // printf("%lld\n%lld\n", SGT.ask(1, -V, V, -114), SGT.ask(1, -V, V, 114));
    // printf("%lld\n%lld\n", SGT.delta(1, -V, V, -114), SGT.delta(1, -V, V, 114));
    // printf("%lld\n", SGT.ask(1, -V, V, 0));
    for (int i = 1;i <= n;++i) {
        int x;scanf("%d", &x);
        l[i] = Less();r[i] = Greater();
        // printf("l r %d %d\n", l[i], r[i]);
        // printf("%lld %lld\n", SGT.delta(1, -V, V, l[i]), SGT.delta(1, -V, V, r[i]));
        // printf("%lld %lld\n", SGT.delta(1, -V, V, l[i] + 1), SGT.delta(1, -V, V, r[i] - 2));
        if (-V <= l[i]) /*printf("Cover [%d, %d] %lld\n", -V, l[i], SGT.ask(1, -V, V, l[i] + 1)), */SGT.cover(1, -V, V, -V, l[i], SGT.ask(1, -V, V, l[i] + 1));
        if (r[i] <= V) /*printf("Cover [%d, %d] %lld\n", r[i], V, SGT.ask(1, -V, V, r[i] - 1)), */SGT.cover(1, -V, V, r[i], V, SGT.ask(1, -V, V, r[i] - 1));
        if (-V <= l[i]) SGT.modify(1, -V, V, -V, l[i], c * (l[i] + V + 1), -c)/*, printf("add [%d, %d] %lld %lld\n", -V, l[i], c * (l[i] + V + 1), -c)*/;
        if (r[i] <= V) SGT.modify(1, -V, V, r[i], V, c, c), SGT.update_delta(1, -V, V, r[i] - 1, c)/*, printf("add [%d, %d] %lld %lld\n", r[i], V, c, c)*/;
        if (-V <= x - 1) SGT.modify(1, -V, V, -V, x - 1, (x + V) * d, -d)/*, printf("add [%d, %d] %lld %lld\n", -V, x - 1, (x + V) * d, -d)*/;
        if (x + 1 <= V) SGT.modify(1, -V, V, x, V, 0, d)/*, printf("add [%d, %d] %lld %lld\n", x, V, 0, d)*/;
        // for (int j = -2;j <= 2;++j) printf("%lld ", SGT.ask(1, -V, V, j));
        // puts("");
    }
    printf("%lld\n", SGT.ask(1, -V, V, find()));
    vector<int>pos;
    int cur = find();
    for (int i = n;i >= 1;--i) {
        ++l[i];--r[i];
        pos.push_back(cur);
        cur = max(l[i], min(cur, r[i]));
    }
    reverse(pos.begin(), pos.end());
    for (auto p : pos) printf("%d ", p);
    return 0;
}
/*
dp[i][j]=max(dp[i-1][k]+|k-j|*c)+|j-x|*d

*/

结语

虽说洛谷评了黑，kenkoooo也给了个 \(3197\) （差 \(3\) 就铜了）吧，但过程都是有迹可循的，不像最近学的 \(\text{Pollard rho}\) 那种及其天马行空，并且相对来说都比较套路（尤其线段树），属于做过一次后相似的题都降一个难度的那种（有的题降了还是不会做(><)）。只不过换个角度来说，这种套路并不常见，将 \(\text{dp}\) 转化为函数也挺巧妙的，学到就是赚到(^^)。