2025杭电多校第八场 最有节目效果的一集、最自律的松鼠、最甜的小情侣、最努力的活着 个人题解

最努力的活着

数学 #高精度

题目

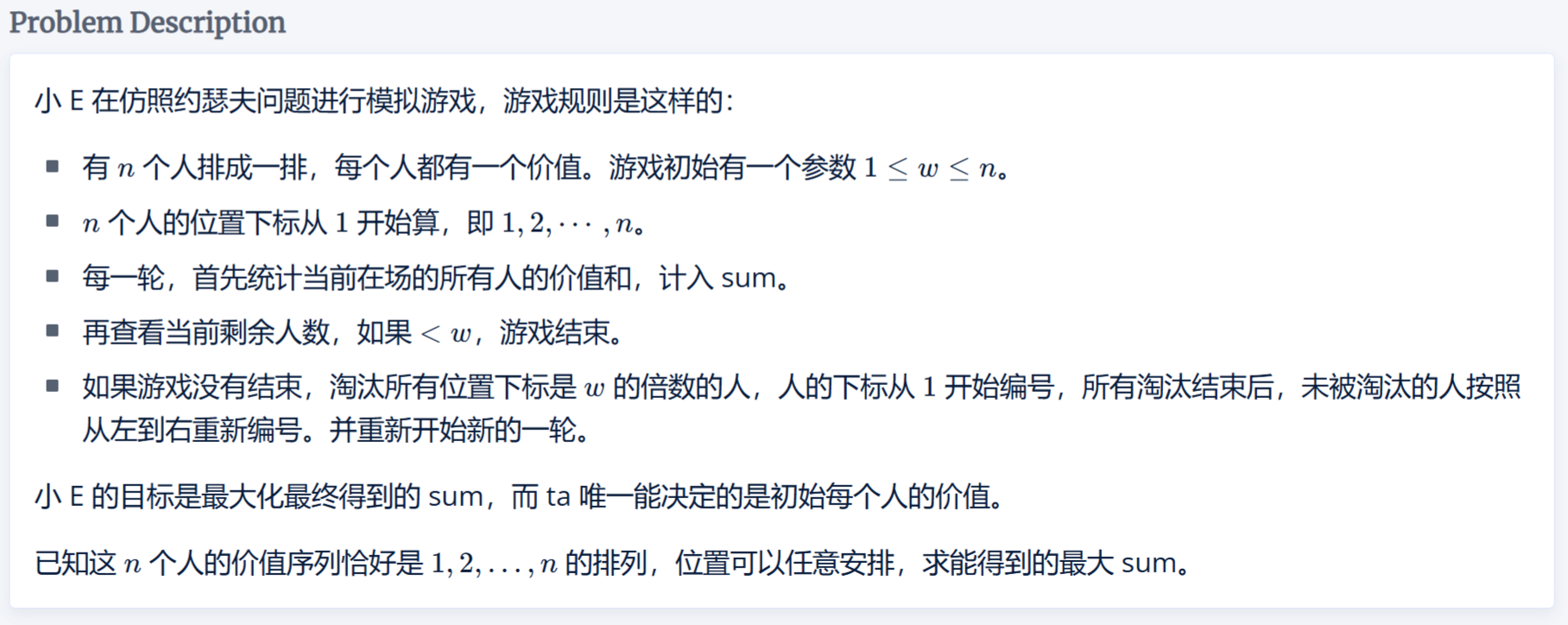
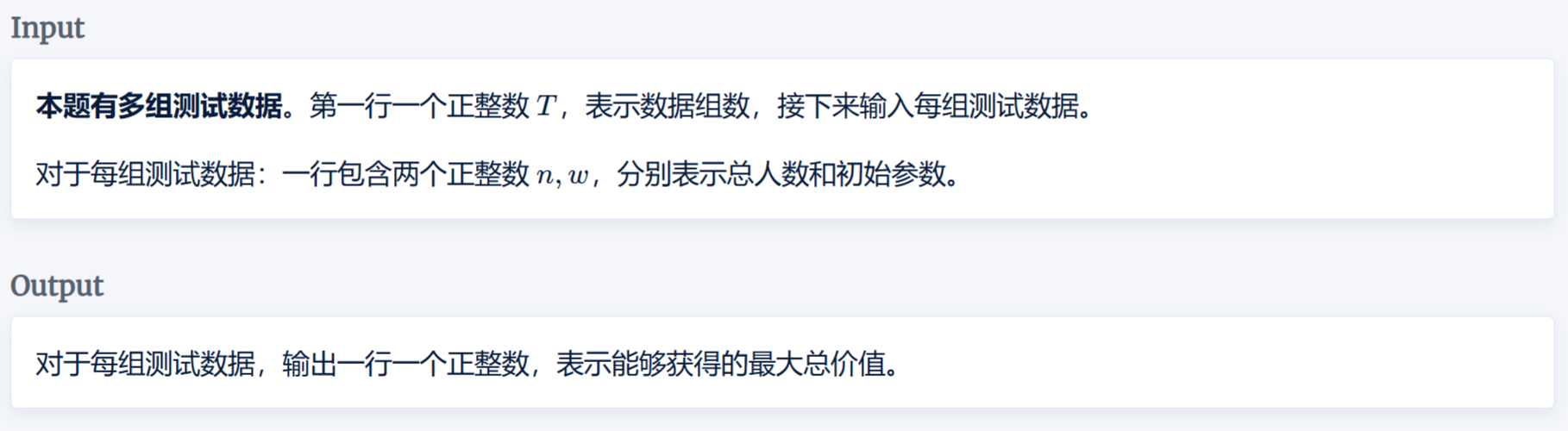
思路

注意到本题给的\(1\leq n\leq 1e 12\)，因此需要使用\(\_\_int 128\)（最大可以存\(2^{128}\)）来提高精度

贪心地想，为了使得最后的答案最大，每次删去的数必然要尽可能小，因此每次删去最小的\(\frac{len}{w}\)个数即可

然而暴力模拟是会\(TLE\)的，因此还需要考虑优化：

设：

• \(cnt:\)当前剩多少数
• \(cnt_{2}:\)删几次
• \(cnt_{3}:\)一次删多少数
  那么对于每一个确定的\(cnt 3\)，我们希望可以计算出一次性算出删掉\(cnt 3\)个数的过程中对答案的贡献\(add\)，因此利用这三个变量进行公式推导：

\[\begin{align} &对于第i次操作 ,剩余的 数为 cnt-i\times cnt_{3}\\ \\ &对于第i次操作,假设剩余k个数,对答案的贡献为n+n-1+\dots+n-k+1=\frac{(2n-k+1)\times k}{2}\\ \\ &将k=cnt-i\times cnt_{3}带入得: \\ \\ add&=\sum_{i=0}^{cnt_{2}-1} [2n-(cnt-i\times cnt_{3})+1]\times(cnt-i\times cnt_{3})\times \frac{1}{2}\\ \\ &=\sum_{i=0}^{cnt_{2}-1}(2n-cnt+1+i\times cnt_{3})\times(cnt-i\times cnt_{3})\times \frac{1}{2}\\ \\ &令A=2n-cnt+1,则:\\ \\ add&=\sum_{i=0}^{cnt_{2}-1}(A+cnt_{3}\times i)\times(-cnt_{3}\times i+cnt)\times \frac{1}{2}\\ \\ &=\sum_{i=0}^{cnt_{2}-1}[-cnt_{3}^2\times i^2+(cnt\times cnt_{3}-A\times cnt_{3})\times i+A\times cnt]\times \frac{1}{2} \end{align} \]

\[\begin{align} &由中学知识:\sum_{i=1}^{n}i^2= \frac{n(n+1)(2n+1)}{6}\\ \\ add&= \left\{ -cnt_{3}^2\times \frac{(cnt_{2}-1)\times cnt_{2}\times (2cnt_{2}-1)}{6}+[cnt\times cnt_{3}-A\times cnt_{3}]\times \frac{cnt_{2}\times(cnt_{2}-1)}{2}+A\times cnt\times cnt_{2} \right\} \times \frac{1}{2} \end{align} \]

因此只需要计算出\(cnt,cnt_{2},cnt_{3}\)即可得到答案！

• \(cnt_{3}\)表示一次删多少数，自然是\(\frac{cnt}{w}\)
• \(cnt_{2}\)表示可以删多少次，\({cnt\%w}\)表示可以用于填补删去的空位的数，则\(\frac{cnt\%w}{cnt_{3}}+1\)代表可以删多少次
• 每次计算完\(add\)之后，需要让当前的\(cnt\)更新，\(cnt-=cnt_{2}\times cnt_{3}\)

代码实现

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<set>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
#define int ll

#define int128 __int128
int128 read() {
    int128 x = 0, w = 1;
    char ch = getchar();
    while (ch < '0' || ch > '9') {if (ch == '-') w = -w;ch = getchar();}
    while (ch >= '0' && ch <= '9') {x = x * 10 + ch - '0';ch = getchar();}
    return w * x;
}
void print(int128 x) {
    if (x < 0) {putchar('-');x = -x;}
    if (x > 9) print(x / 10);
    putchar(x % 10 + '0');
}

void eachT() {
    int nn,ww;cin>>nn>>ww;
    int128 n=nn,w=ww,cnt=n,sum=0,cnt2=0,cnt3=0;
    while(1){
        int128 A=2*n-cnt+1;
        cnt3 = cnt/w;
        if(cnt3==0){
            sum += A*cnt/2;
            break;
        }
        cnt2 = cnt%w/cnt3+1;
        int128 add=(-cnt3*cnt3*(cnt2-1)*cnt2*(2*cnt2-1)/6+(cnt*cnt3-A*cnt3)*cnt2*(cnt2-1)/2+A*cnt*cnt2)/2;
        sum+=add;
        if(cnt<w)break;
        cnt-=cnt3*cnt2;
    } 
    print(sum);
    cout<<'\n';
}

signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--) eachT();
}

---

最甜的小情侣

线段树 #线段树维护矩阵 #dp #线性dp

题目

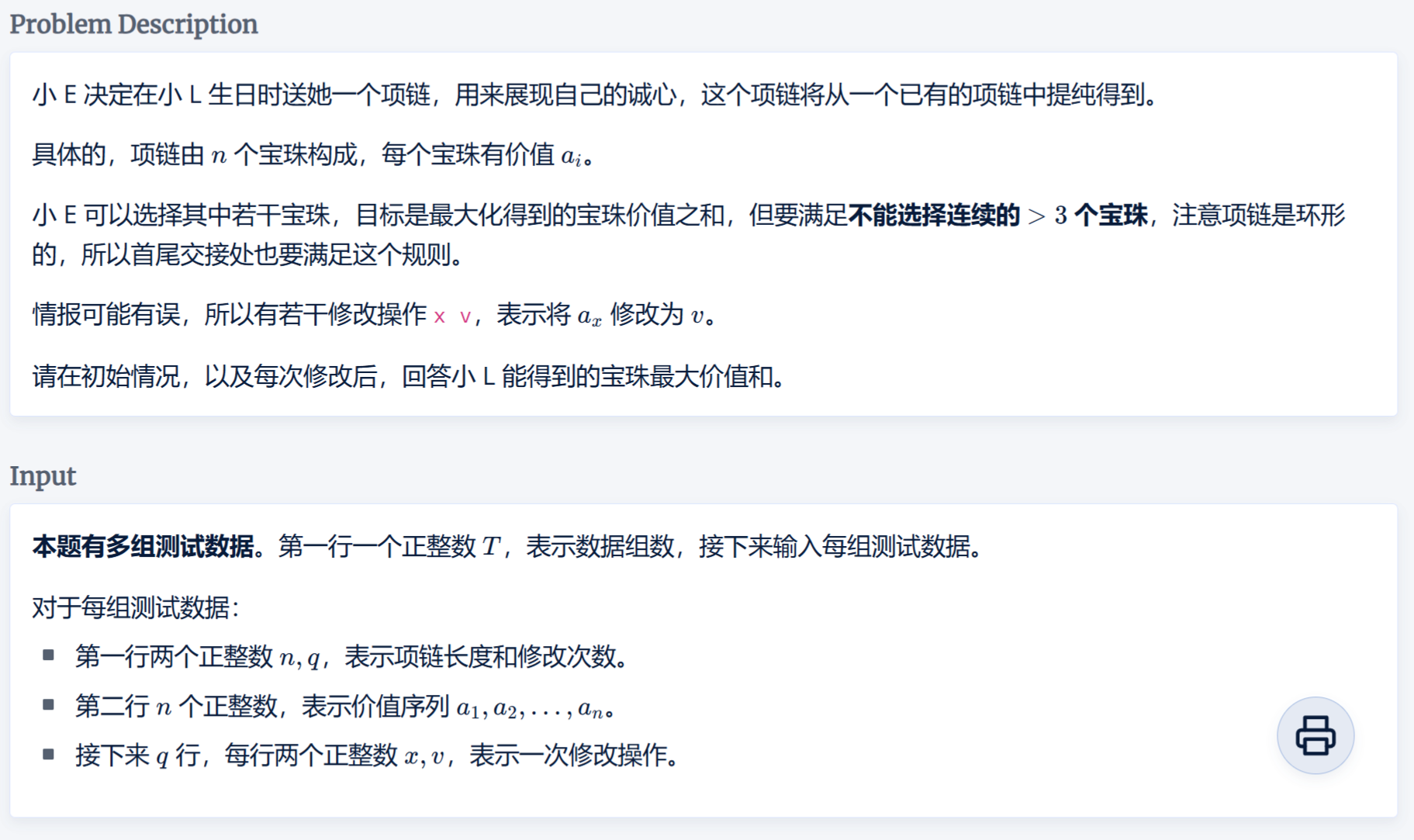
思路

在不考虑修改操作的时候，我们可以很快写出线性递推：

• 状态表示：
  • \(dp[i][j]\)表示\(1\sim i\)中，第\(i\)位是连续的第\(j\)个宝珠，宝珠最大价值和
• 状态转移：

\[\begin{align} &dp[i][0]=\max_{0\leq j\leq 3}\{\ dp[i-1][j] \ \}\\ \\ &dp[i][j]=dp[i-1][j-1]\ \ (1\leq j\leq 3) \end{align} \]

但是本题加入了单点修改操作，这要求我们在\(o(\log n)\)的复杂度内解决每一次修改与查询

因此很自然想到了使用线段树一类的数据结构来维护dp信息

线性dp的状态转移实际上可以看作\(dp[i]=f(dp[i-1])\)，其中\(f(x)\)为对于\(x\)的某种变换

创建一个变换矩阵 \(A\)，那么上式可以写作\(dp[i]=A\times dp[i-1]\)

本题中，\(dp[i]\)是一个四维的列向量：

\[dp[i]_{4\times 1}= \begin{pmatrix} dp[i][0]\\ dp[i][1] \\ dp[i][2] \\ dp[i][3] \end{pmatrix} \]

因此可以尝试构造一个变换矩阵\(A\)描述状态转移：

\[\begin{align} dp[i]{4\times 1}&=A{4\times 4}\times dp[i-1]_{4\times 1}\\ \\ \begin{pmatrix} dp[i][0]\\ dp[i][1] \\ dp[i][2] \\ dp[i][3] \end{pmatrix}&= \begin{pmatrix} \ ?\quad?\quad?\quad?\ \\ \ ?\quad?\quad?\quad?\ \\ \ ?\quad?\quad?\quad?\ \\ \ ?\quad?\quad?\quad?\ \end{pmatrix} \times \begin{pmatrix} dp[i-1][0]\\ dp[i-1][1] \\ dp[i-1][2] \\ dp[i-1][3] \end{pmatrix} \end{align} \]

为了描述取\(max\)运算的过程，需要对矩阵内的运算进行重载：

\[\begin{align} &a+b\to max\{ a,b \}\\ \\ &a\times b\to a+b \end{align} \]

此时可以通过观察构造出变换矩阵：

\[\begin{align} \begin{pmatrix} dp[i][0]\\ dp[i][1] \\ dp[i][2] \\ dp[i][3] \end{pmatrix}&= \left( \begin{array}{rc} &0 &0 &0 &0\\ &-inf &w[i] &-inf &-inf \\ &-inf &-inf &w[i] &-inf \\ &-inf &-inf &-inf &w[i] \end{array} \right) \times \begin{pmatrix} dp[i-1][0]\\ dp[i-1][1] \\ dp[i-1][2] \\ dp[i-1][3] \end{pmatrix} \end{align} \]

对于一个区间\([l,r]\)，可以通过线段树维护从\(l\)到\(r\)上所有的矩阵\(A\)的乘积\(A_{l}A_{l+1}···A_{r}=A_{l\sim r}\)

则可以进行\(pushup\)操作：

\[A_{l\sim r}=A_{l\sim mid}\times A_{mid+1\sim r} \]

用线段树维护累乘信息即可

解决了修改问题，还剩下一个问题没有解决：该过程在环上进行

一般的思路是将序列倍增，滑动窗口解决

但是本题不允许使用滑动窗口+线段树每次询问\(o(n\log n)\)的复杂度，因此需要考虑其他优化

而注意到限制条件中的连续数量不大于3，可以考虑分类！

仍然先让序列倍增至\(2n\)，对开头的几个元素进行分类：

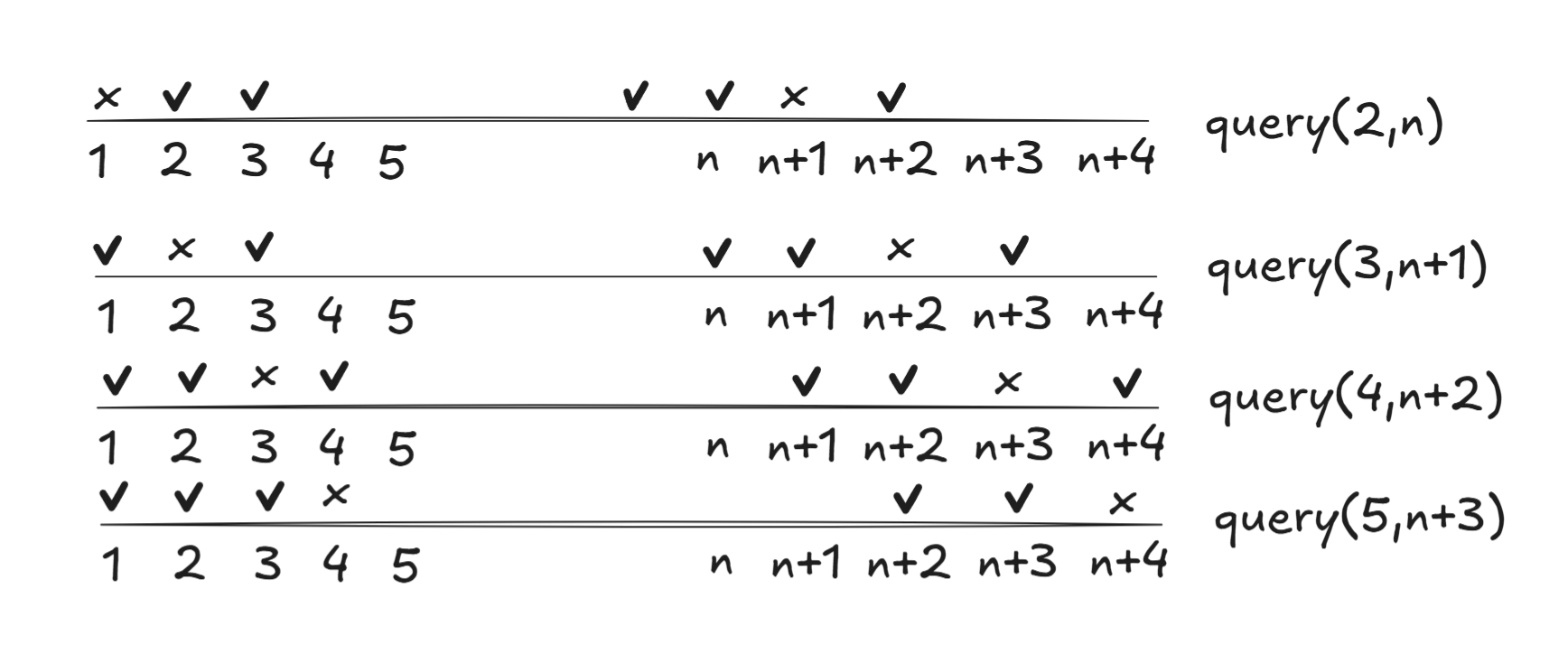
×代表该位置不选宝珠，√代表该位置选宝珠

由此可以通过四个分类将环形问题的连接处的所有情况考虑到，不需要倍增，只需要维护\(1\sim n+3\)的序列

但是，每次都查询四个区间，\(4\log n\)的复杂度将导致常数过大，会被卡常

因此需要取四个查询的交集，即\([5,n]\)，每次只查询这个区间，其他的区间可以直接\(o(1)\)调用其线段树节点所维护的矩阵，再进行矩阵乘法

在取出区间\([l,r]\)上的矩阵后，我们需要拿一个全零的列向量与其相乘，随后取答案向量四个维度的最大值

然而我们重定义了乘法为取最大值，因此全零向量作乘法实际上就是在对矩阵的所有元素取最大值

因此只需要将整个矩阵中的所有元素取\(max\)即可完成一次查询

代码实现

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<unordered_map>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
#define int ll
const int inf=1e18;
const int N=2e5+15;

unordered_map<int,int>id;

struct M {
    int size;
    int data[4][4];
    M() : size(4){
        rep(i,0,3)rep(j,0,3)data[i][j]=-inf;
    }
    M operator*(const M& other) const {
        M res;
        rep(i, 0, size - 1) {
            rep(j, 0, size - 1) {
                rep(k, 0, size - 1) {
                    res.data[i][j] = max(res.data[i][j], data[i][k] + other.data[k][j]);
                }
            }
        }
        return res;
    }
    void init(int w){
        int tmp[4][4]={{0,0,0,0},{w,-inf,-inf,-inf},{-inf,w,-inf,-inf},{-inf,-inf,w,-inf}};
        rep(i,0,3)rep(j,0,3)data[i][j]=tmp[i][j];
    }
};

#define lc p<<1
#define rc p<<1|1
#define mid ((l+r)>>1)
int ls[N<<2],rs[N<<2],w[N];
M m[N<<2];
int n,q;

void pushup(int p){
    m[p]=m[lc]*m[rc];
}

void build(int p,int l,int r){  
    if(l==r){
        m[p].init(w[l]);
        if(l<=4)id[l]=p;
        if(n+1<=l&&l<=n+3)id[l]=p;
        return;
    }    
    build(lc,l,mid),build(rc,mid+1,r);
    pushup(p);
}

void update(int p,int l,int r,int pos,int val){
    if(l==r){m[p].init(val);return;}
    if(pos<=mid)update(lc,l,mid,pos,val);
    else update(rc,mid+1,r,pos,val);
    pushup(p);
}

M query(int p,int l,int r,int x,int y){
    if(x<=l&&r<=y)return m[p];
    M res1,res2;
    bool L=0,R=0;
    if(x<=mid)res1=query(lc,l,mid,x,y),L=1;
    if(y>mid)res2=query(rc,mid+1,r,x,y),R=1;
    if(L&&R)return res1*res2;
    if(L)return res1;
    if(R)return res2;
}

int getans(M&t){
    int res=0;
    rep(i,0,3)rep(j,0,3)res=max(res,t.data[i][j]);
    return res;
}

void maxans(int&ans){
    M t=query(1,1,n+10,5,n);
    M p=m[id[2]]*m[id[3]]*m[id[4]]*t;
    ans=max(ans,getans(p));
    p=m[id[3]]*m[id[4]]*t*m[id[n+1]];
    ans=max(ans,getans(p));
    p=m[id[4]]*t*m[id[n+1]]*m[id[n+2]];
    ans=max(ans,getans(p));
    p=t*m[id[n+1]]*m[id[n+2]]*m[id[n+3]];
    ans=max(ans,getans(p));
}

void eachT() {
    cin>>n>>q;
    rep(i,1,n){
        cin>>w[i];
        if(i<=10)w[i+n]=w[i];
    }
    build(1,1,n+10);
    int ans=0;
    maxans(ans);
    cout<<ans<<'\n';
    rep(i,1,q){
        int x,v;cin>>x>>v;
        update(1,1,n+10,x,v);
        if(x<=10)update(1,1,n+10,x+n,v);
        int ans=0;
        maxans(ans);
        cout<<ans<<'\n';
    }
}

signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--) eachT();
}

---

最自律的松鼠

模拟

题目

思路

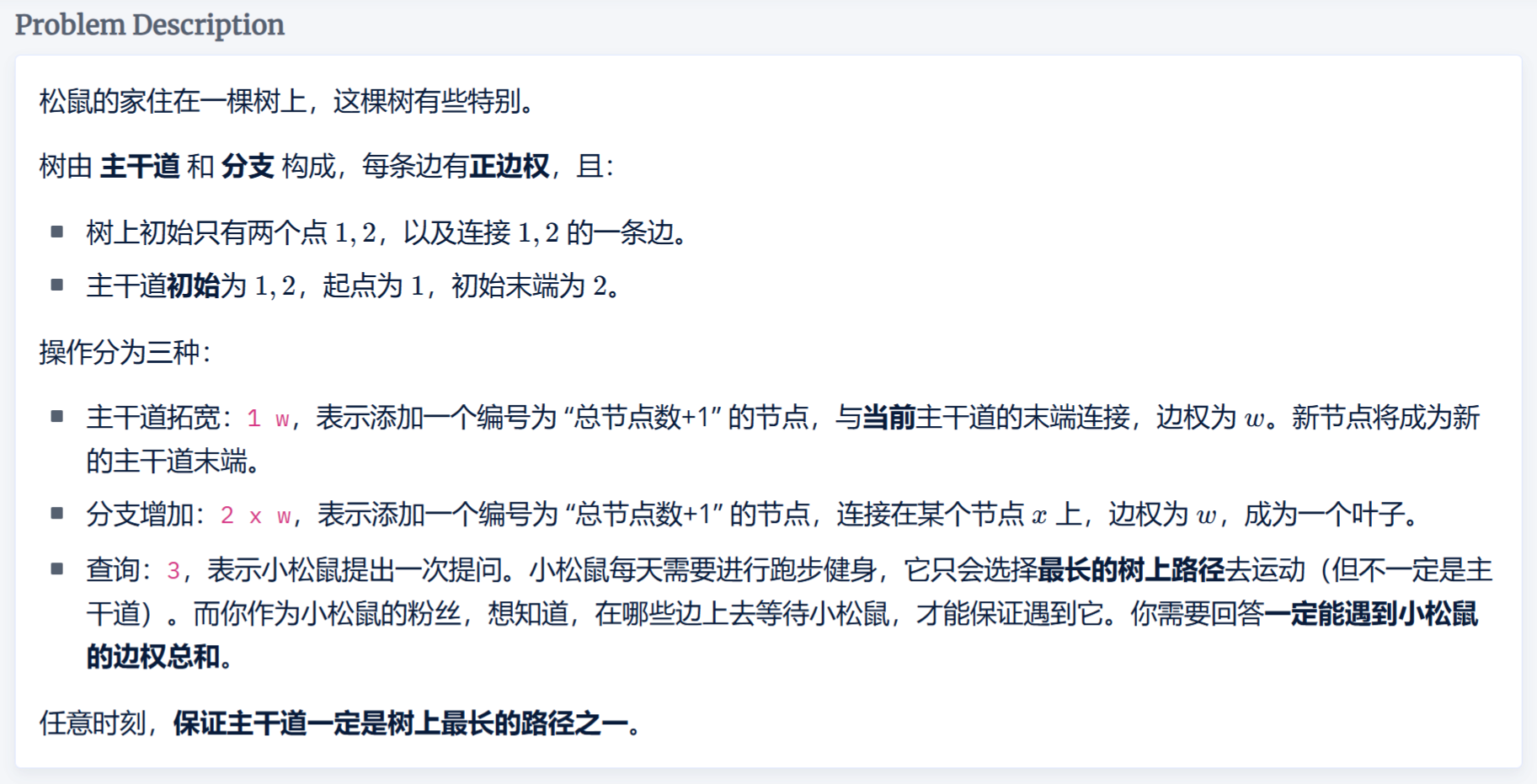
如果将图进行简化，绿线代表主干道，黄线代表从主干道上延伸出去的支路

考虑一种特殊情况：

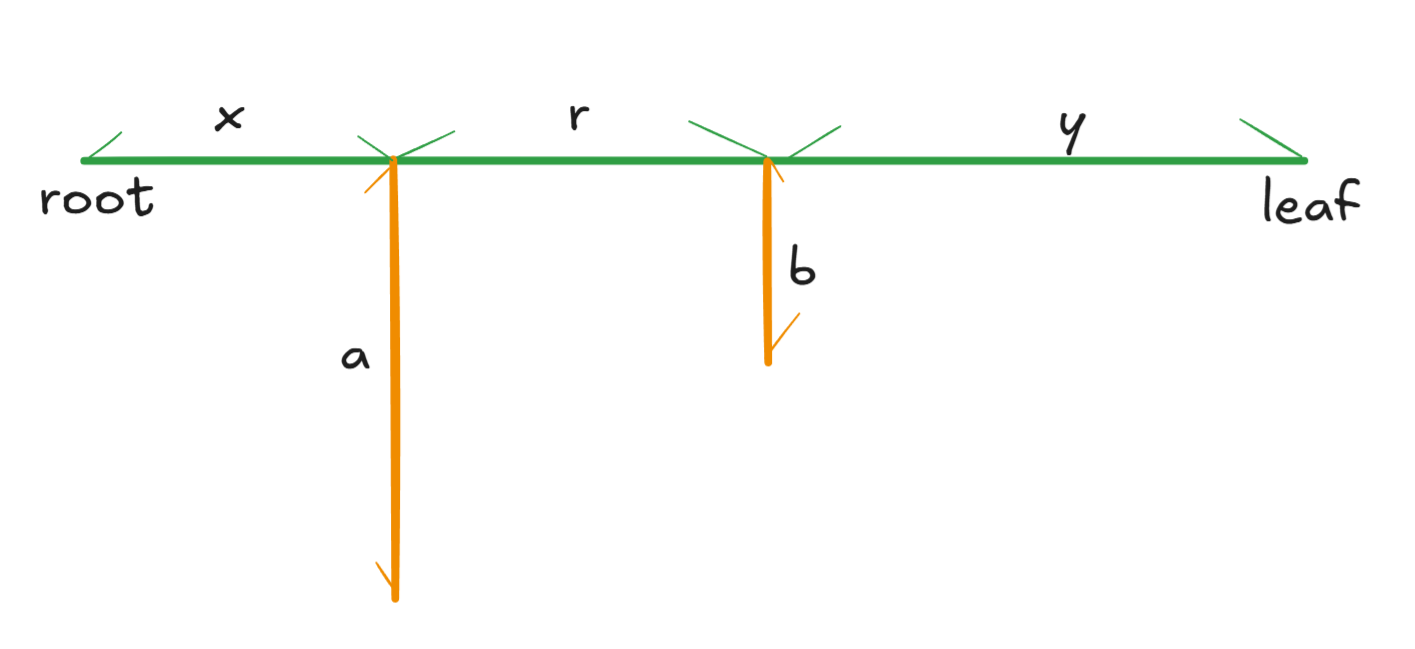
\[\begin{align} &假设x<a,b<y\\ \\ &则有x+b<y+a\\ \\ &x+b+r<y+a+r\\ \\ &x+y+r<x+b+r<y+a+r\\ \\ &然而所有支路长度不得大于主干道,因此假设不成立\\ \\ &因此有x\geq a,y\geq b \end{align} \]

同理可证\(x\leq a,y\leq b\)

因此有\(x=a,y=b\)

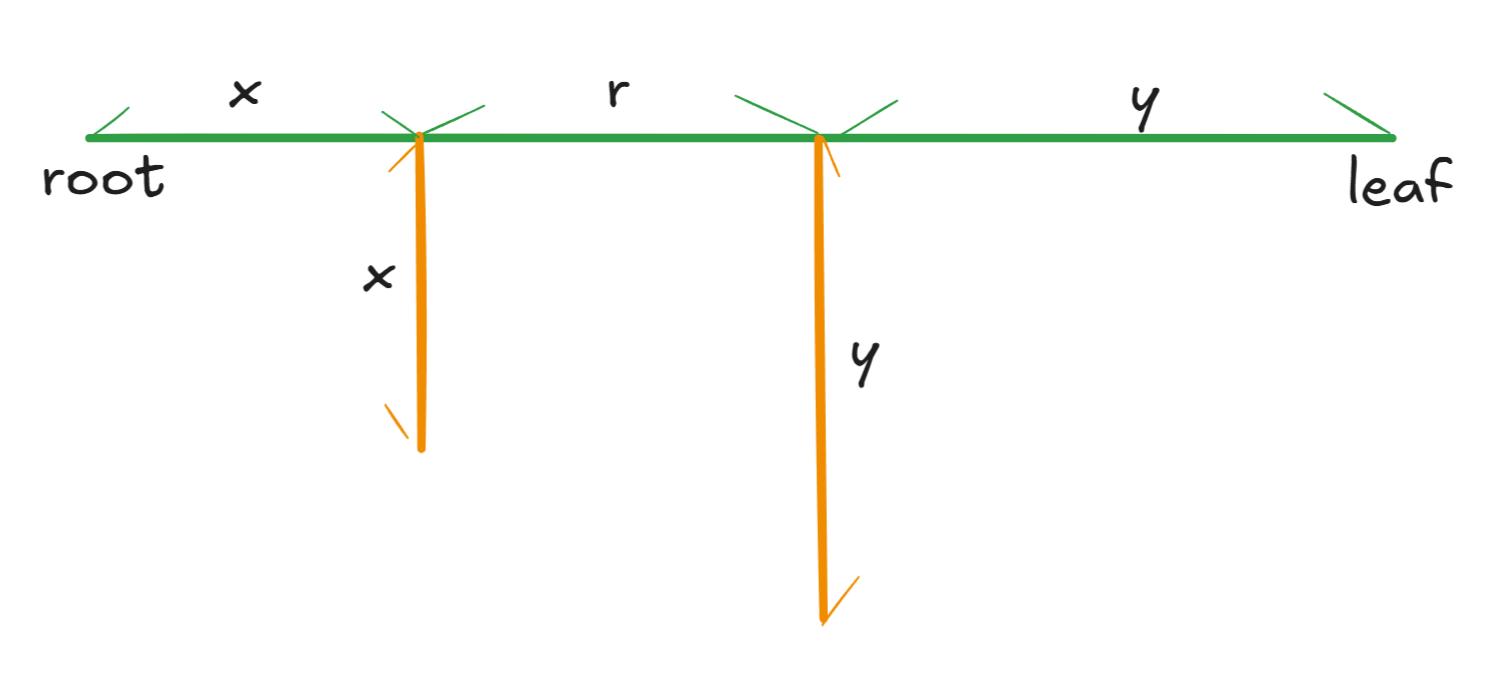
因此每次对支路新增节点只需维护其子树的最大深度即可

易知，能够作为等待边的必然在主干路上，而上图中的\(r\)段就是一个可能区域

我们的目标便是找到所有\(r\)段的交集

因此，设置\(l\)从左向右更新，维护最靠右的合法支路；设置\(r\)从右向左更新，维护最靠左的合法支路

对于一个查询，直接输出主干路上的\([l,r]\)上的区间和即可

当然，如果出现了\(r\leq l\)的情况，那么就直接输出0即可

代码实现

#include<iostream>
#include<cstdio>
#include<vector>
#include<algorithm>
#include<unordered_map>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
#define int ll
const int inf=1e18;
const int N=5e5+15;
int n,w,root,leaf,tot,l,r;

struct node{
    int dep,rt;
}a[N];

int maxdep[N],pre[N];

void eachT() {
    cin>>n>>w;
    root=1,leaf=2,tot=2,l=1,r=2;
    maxdep[1]=maxdep[2]=0;
    a[1].dep=a[2].dep=0;
    a[1].rt=a[2].rt=0;

    rep(i,1,n){
        pre[i]=maxdep[i]=0;
    }
    pre[2]=w;
    unordered_map<int,int>id;
    int main=2;
    id[1]=1,id[2]=2;

    rep(i,1,n){
        int op;cin>>op;
        if(op==1){
            tot++;
            int w;cin>>w;
            id[tot]=++main;
            pre[main]=pre[main-1]+w;
            leaf=tot;
            a[leaf].dep=a[leaf].rt=0;
            r=main;
        }else if(op==2){
            tot++;
            int x,w;cin>>x>>w;
            a[tot].dep=a[x].dep+w;
            if(a[x].rt==0)a[tot].rt=x;
            else a[tot].rt=a[x].rt;
            int rt=a[tot].rt;
            maxdep[rt]=max(maxdep[rt],a[tot].dep);
            if(maxdep[rt]==pre[id[rt]])l=max(l,id[rt]);
            if(maxdep[rt]==pre[main]-pre[id[rt]])r=min(r,id[rt]);
        }else{
            if(l>=r)cout<<0<<'\n';
            else cout<<pre[r]-pre[l]<<'\n';
        }
    }
}

signed main() {
    ios::sync_with_stdio(0);
    cin.tie(0), cout.tie(0);
    int t = 1;
    cin >> t;
    while (t--) eachT();
}

---

最有节目效果的一集

平衡树 #红黑树 #模拟

题目

思路

本题为模拟题，关键在于面向对象以及排名的修改查询的实现

结构体\(Team\)：

• \(win\ num\)：该队伍赢的局数
• \(win\ score\)：该队伍的净胜分
• \(group\)：该队伍属于哪个组
• \(name\)：该队伍的名字
• \(team\ cmp\)：三关键字的比较函数

\(Team\)类数组\(team[3\times N]\)，用于储存所有队伍的信息

红黑树\(orderd\ set\)，简称\(os\)，开三棵用于维护三个组的\(Team\)，其中的比较函数采用\(team \ cmp\)

结构体\(Information\)：

• \(team_{1},team_{2}\)：信息中的两个队伍
• \(score_{1},score_{2}\)两个队伍对应的比分
• \(time\)：该信息出现的时间
• 比较函数：以\(time\)为关键字比较

\(Information\)类数组\(info[M]\)，用于储存所有的论坛信息

\(bool\)型数组\(del[M]\)，用于标记当前信息是否已经被删除
\(map\langle \ pair\langle string,string\rangle\ ,\ set\langle Information\ \rangle\ \rangle mp\)，其中\(mp[\ \{ A,B \}\ ]\)代表关于 \(A,B\)两个队伍的论坛信息集合，按照时间升序排序

\(hash\langle\ string,int\ \rangle id\_people,id\_team\)，分别表示某成员所在队伍的编号、某队伍的编号

相信读者在理解所有使用的\(stl\)与结构体后，都能自己想到怎么模拟这个过程了，在此不过多赘述

但其中有部分细节需要注意：

• 无效信息不得放入\(mp\)中，否则会引起错误
• 写一个\(change\)函数用于修改红黑树中的值，先删去原有的值，修改完毕后再插入回去
• 题目有可能多次删除同一条信息，因此需要\(del[M]\)数组
• 在删除信息的时候，需要判断删除的是否是正在使用的信息
• 需要对删除信息之后集合是否非空进行特判
• 红黑树的\(.order\_of\_key()\)函数返回的是\(0-based\)下标，答案需要+1得到排名

代码实现

#include<iostream>
#include<vector>
#include<map>
#include<cmath>
#include<set>
using namespace std;
using ll = long long;
#define rep(i, a, b) for(int i = (a); i <= (b); i ++)
#define per(i, a, b) for(int i = (a); i >= (b); i --)
#define see(stl) for(auto&ele:stl)cout<<ele<<" "; cout<<'\n';
constexpr ll inf = 1e9 + 5;
// #define int ll 

const int N=1e3+5,M=1e5+5;
int n,k;

#include <ext/pb_ds/assoc_container.hpp>
#include <ext/pb_ds/tree_policy.hpp>
using namespace __gnu_pbds;

gp_hash_table<string,int>id_pp,id_team;

struct Team{
    int winnum,winscore,group;
    string name;
    void print(){
        cout<<"name:"<<name<<" winnum:"<<winnum<<" winscore:"<<winscore<<" group:"<<group<<endl;
    }
}team[3*N];
struct teamcmp{
    bool operator()(const Team&a,const Team&b)const{
        if(a.winnum!=b.winnum)return a.winnum>b.winnum;
        if(a.winscore!=b.winscore)return a.winscore>b.winscore;
        return a.name<b.name;
    }
};
tree<
    Team, 
    null_type, 
    teamcmp, 
    rb_tree_tag, 
    tree_order_statistics_node_update
>os[4];

struct Info{
    string team1,team2;
    int score1,score2,tim;
    bool operator<(const Info&t)const{
        return tim<t.tim;
    }
}info[M];
bool del[M];
map<pair<string,string>,set<Info>>mp;

void change(string A,string B,int Ascore,int Bscore,int ida,int idb,int pd){
    if(A>B)swap(A,B),swap(Ascore,Bscore);  
    os[ida].erase(team[id_team[A]]);
    os[idb].erase(team[id_team[B]]);
    team[id_team[A]].winnum+=(Ascore>Bscore)*pd;
    team[id_team[B]].winnum+=(Bscore>Ascore)*pd;
    team[id_team[A]].winscore+=(Ascore-Bscore)*pd;
    team[id_team[B]].winscore+=(Bscore-Ascore)*pd;
    os[ida].insert(team[id_team[A]]);
    os[idb].insert(team[id_team[B]]);
}

void read(string&A,string&B,int&Ascore,int&Bscore){
    string x;
    rep(i,1,3)cin>>x;
    cin>>x;
    x.pop_back();
    A=x;
    rep(i,1,7)cin>>x;
    cin>>x;
    B=x;
    cin>>x;cin>>x;
    Ascore=x[0]-'0';
    Bscore=x[2]-'0';
}

void eachT() {   
    cin>>n>>k;

    id_pp.clear();
    id_team.clear();
    mp.clear();
    rep(i,1,3)os[i].clear();
    rep(i,1,3*n)del[i]=0;

    rep(i,1,3*n){
        string tm;cin>>tm;      
        rep(j,0,4){
            string x;cin>>x;
            id_pp[x]=i;
        }
        int group;cin>>group;
        id_team[tm]=i;
        team[i]={0,0,group,tm};
        os[group].insert(team[i]);
    }
    int tim=0;
    rep(i,1,k){
        int op;cin>>op;
        if(op==1){
            tim++;
            string A,B;int Ascore,Bscore;        
            read(A,B,Ascore,Bscore);
            
            if(id_team[A]==0)A=team[id_pp[A]].name;
            if(A>B)swap(A,B),swap(Ascore,Bscore);

            info[tim]={A,B,Ascore,Bscore,tim};
            del[tim]=0;
            int ida=team[id_team[A]].group,idb=team[id_team[B]].group;
            if(ida!=idb)continue;//无效信息

            mp[{A,B}].insert(info[tim]);
            if(mp[{A,B}].size()==1){
                change(A,B,Ascore,Bscore,ida,idb,1);
            }
        }else if(op==2){
            int x;cin>>x;
            string A=info[x].team1,B=info[x].team2;
            if(A>B)swap(A,B);
            int ida=team[id_team[A]].group,idb=team[id_team[B]].group;
            if(ida!=idb)continue;//无效信息

            if(del[x])continue;
            del[x]=1;
            Info now=*mp[{A,B}].begin();
            if(info[x].tim==now.tim){//删掉的刚好是正在使用的信息
                change(A,B,now.score1,now.score2,ida,idb,-1);
                mp[{A,B}].erase(info[x]);          
                if(mp[{A,B}].empty())continue;

                Info modify=*mp[{A,B}].begin();
                int Ascore=modify.score1,Bscore=modify.score2;
                change(A,B,Ascore,Bscore,ida,idb,1);
            }else{
                mp[{A,B}].erase(info[x]);
            }
        }else{//op==3
            int x;cin>>x;
            int group=team[x].group;
            cout<<os[group].order_of_key(team[x])+1<<'\n';
        }
    }
}

signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0), cout.tie(0);
    ll t = 1;
    cin >> t;
    while (t--) {
        eachT();
    }
}