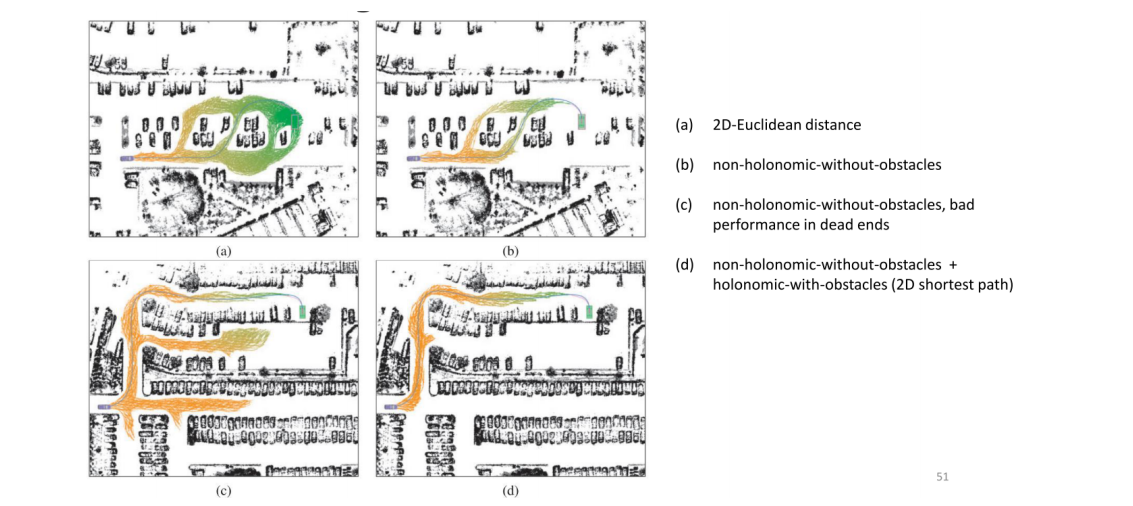
本文学习自南京理工大学算法组的文章。融入自己的一点思考,仅学习用。
常见的路径规划方法有:
基于采样的算法如RRT*(快速随机生成树)
基于搜索的算法如A*,Dijkstra,HybridA*
传统A*算法
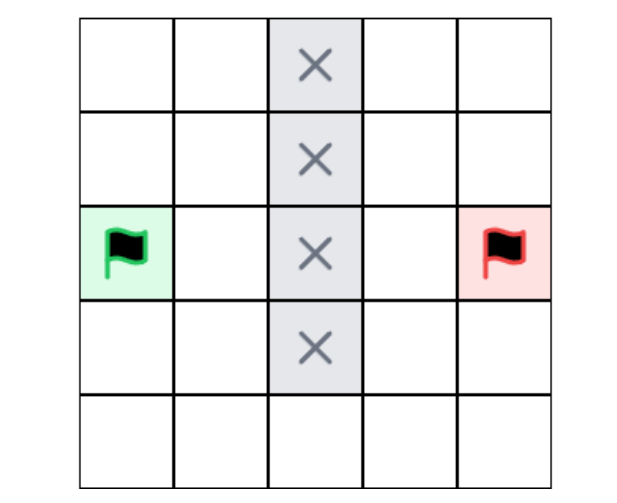
真实的地图变化成栅格地图
绿色旗帜搜索一条到达红色旗帜的路径,机器人只可以上下左右进行移动。
采样方法:
对于一个格子,他可以达到的是周围的 4 个(因为只可以上下左右移动)可到达格子。
每个格子在被拓展的时候。记录下它上一步的格子。

上下左右的四个点构成的集合称为OpenList
已经走过的点的集合称为CloseList
那么每次拓展的格子,就是从OpenList中拿一个格子进行拓展
同时拿掉CloseList之外的点
现在我们用一个新的角度来理解上面的行为,注意,接下来的内容很绕,但是十分重要,如
果说每个格子代表一个状态,包括: x,y,parent 三个信息,那么,每次更新,就是在可以到达的
格子中选取一个格子,然后,通过我们规定的控制量:上,下,左,右,采样出四个点,当然,
因为有些点达不到或者已经到达了不会每次拓展 4 个点,将采样到的点添加进入 OpenList 中,
这就是全过程,重点来了,既然我们可以通过控制量采样,是否也能进行状态量的采样,然后
计算出到达这个状态的路径,这是可行的,但这并非我们的重点。
open_list 是一个优先队列,用于存储待处理的节点。这些节点是算法接下来将要探索的候选节点。 open_list 中的节点按照它们的 f 值(即从起点到当前节点的实际代价 g 加上从当前节点到目标节点的估计代价 h )进行排序, f 值最小的节点被认为是最有可能引领到目标节点的路径。
closed_list 是一个集合,用于存储已经被评估过的节点。这些节点在搜索过程中被扩展过,并且不再需要进一步探索
启发函数h(n)
现在我们得到了四个候选的格子,我们现在的目标是选出最有可能到达目的地的格子,显
然,单纯的四个格子没有办法获取到,那么,我们只要给每个格子赋个值,然后选择最有可能
到达的点优先进行拓展
为了达到这个目的,我们引入了启发函数 h(n) ,普通 A* 中最常见的 h(n) 为曼哈顿距离,公
式为

target 为目标点, n 为当前点
举个简单的例子:当前点 n 的坐标为(2,3),目标点 target 的坐标为(5,5)
计算的得到曼哈顿距离为5,也就是最短路径需要5步。
注意!启发函数除了曼哈顿距离 还有平方后欧式距离
抵达代价:
按照刚才启发函数的思路,你越来越靠近目标,应该h(n)越来越小。
但是可能会出现两种情况:
一:存在障碍物的话,绿棋会先到达障碍物边然后重新搜索,绕着障碍物边缘走,很明显这样的路径不会是最短的
二:有可能遇到两个节点拓展到同一节点,需要重新确定新节点的父节点。

这时需要抵达代价函数,这个函数的实际意义是,目前到达这个格子实际花费的
代价, g(n) 的计算方法是:

其中 calc _ g 函数是计算点 n 和点 parent 之间增加了多少的代价,也可以表示为 ,因为 A*
是按照网格搜索的,因此只要把一路上的加起来便是
OpenList 中的格子代价变为

, 这样一来,每个点的代价得到了一个比较正确的预估,因为相同格子的 h(n) 必然相同,而 g(n)
与到达该格子的实际花费有关。
大白话就是,有了代价函数。A*算法能够追踪从起点到每个节点的累积代价,并选择代价最小的路径继续搜索,从而找到从起点到目标点的最短路径。
那这样能保证不会绕弯吗,并不能保证。
是否得到最短路径,取决于 h(n)和 g(n)的关系,以及OpenList的实现方式。
**h(n)与g(n)**大小与寻路效果的影响与原因
如果

那么走的远的点的代价一定大于走的近的点,此时会倾向于在近处多搜索,这样得到的路径必
然最短,但是会搜索更多的格子
如果

此时走的远的点的代价一定小于走的近的点,此时会倾向于在末端处多搜索,这样得到的路径
可能不是最短 , 如下图所示

当

此时算法的行为取决于你的 OpenList 如何编写,一般我们在工程上会把 OpenList 实现为一个
插入到相同项后的优先队列,也就是优先队列本身存在时间上的关系,这样可以保证在值相同
时,优先搜索靠近的点 , 虽然前面提到最好是新元素在后,但是其实影响不大,当你无法断定使
用的类是否符合的时候可以不管
由上面的介绍,可以发现,A* 算法是一个结合了广度优先搜索和贪心策略的搜索方式,h(n)
的值代表了该点到达目的地的期望价值,但是,期望上离得最近的点,在直线上存在障碍物的
时候就不再是全局最优的点,因此我们引入了 g(n),将 h(n) 与 g(n) 结合,就有了期望上全局起
点到终点的最小代价,这样我们每次选择的点就更加接近全局最优
同时也可以发现,
当 h(n)−>0; g(n )! = 0, A* 退化为广度优先搜索
当 g(n)−>0; h(n )! = 0, A* 退化为贪婪选择局部最优的搜索方法
算法流程
输入为一个起点,一个终点,从起点开始,把起点加入 OpenList, 开始主循环
主循环:
• 从 OpenList 中取出最优点放入 CloseList
• 调用顶部点的采样方法,获得 4 个新点,每个点在被采样时计算自己的 G 和 H 的信息
• 获得的点检查是否满足在地图中,不在不可到达区域,且不在 CloseList 中
• 满足条件的点加入 OpenList
• 是否找到终点或者 OpenList 中不存在点跳出主循环
跳出后:如果找到目标点,根据 Parent 的内容递归地获取一条路径,如果没有找到目标点,返
回无。
代码如下:
#include <iostream>
#include <vector>
#include <queue>
#include <cmath>
#include <unordered_set>
#include <functional>
using namespace std;
struct Node {
int x, y; // 节点坐标
int g; // 从起点到当前节点的代价
int h; // 启发式估计的从当前节点到终点的代价(启发函数)
int f; // 总代价(g+h)
Node* parent; // 父节点指针
// 构造函数
Node(int x, int y, Node* parent = nullptr) : x(x), y(y), parent(parent) {
g = h = f = 0;
}
// 用于优先队列的比较函数
bool operator>(const Node& rhs) const {
return f > rhs.f;
}
};
// 启发式函数(曼哈顿距离)
int heuristic(const Node& a, const Node& b) {
return abs(a.x - b.x) + abs(a.y - b.y);
}
// 检查位置是否有效(在迷宫内、不是障碍物、不在closed_set中)
bool isValid(int x, int y, const vector<vector<char>>& maze, unordered_set<pair<int, int>>& closed_set) {
if (x < 0 || y < 0 || x >= maze.size() || y >= maze[0].size() || maze[x][y] == '1' || closed_set.count({x, y})) {
return false;
}
return true;
}
// A*算法实现
vector<pair<int, int>> astar(const vector<vector<char>>& maze, pair<int, int> start, pair<int, int> end) {
priority_queue<Node, vector<Node>, greater<Node>> open_list; // 优先队列,用于存储open_list
unordered_set<pair<int, int>> closed_set; // 用于存储已经访问过的节点
Node start_node(start.first, start.second, nullptr); // 起点节点
// 计算起点到终点的启发式代价
start_node.h = heuristic(start_node, Node(end.first, end.second));
// 初始化f值
start_node.f = start_node.h;
// 将起点加入open_list
open_list.push(start_node);
// 四个方向:下、上、右、左
vector<vector<int>> directions = {{1, 0}, {-1, 0}, {0, 1}, {0, -1}};
while (!open_list.empty()) {
Node current = open_list.top(); // 从open_list中取出f值最小的节点
open_list.pop();
closed_set.insert({current.x, current.y}); // 将当前节点加入closed_set
// 如果当前节点是终点,则重建路径并返回
if (current.x == end.first && current.y == end.second) {
vector<pair<int, int>> path;
// 从终点回溯到起点,重建路径
while (current.parent) {
path.push_back({current.x, current.y});
current = *current.parent;
}
// 添加起点到路径
path.push_back({current.x, current.y});
// 反转路径,使其从起点到终点
reverse(path.begin(), path.end());
return path;
}
// 扩展当前节点的四个邻居
for (auto& dir : directions) {
int next_x = current.x + dir[0];
int next_y = current.y + dir[1];
// 检查邻居是否有效
if (isValid(next_x, next_y, maze, closed_set)) {
// 创建邻居节点
Node next_node(next_x, next_y, ¤t);
// 计算邻居节点的g值
next_node.g = current.g + 1;
// 计算邻居节点的h值
next_node.h = heuristic(next_node, Node(end.first, end.second));
// 计算邻居节点的f值
next_node.f = next_node.g + next_node.h;
// 如果邻居节点不在closed_set中
if (closed_set.count({next_x, next_y}) == 0) {
// 将邻居节点加入open_list
open_list.push(next_node);
}
}
}
}
return {}; // 如果没有找到路径,返回空路径
}
int main() {
vector<vector<char>> maze = {
{'0', '0', '1', '0', '0'},
{'0', '0', '1', '0', '0'},
{'0', '0', '0', '1', '0'},
{'0', '0', '1', '1', '0'},
{'0', '0', '0', '0', '0'}
};
pair<int, int> start = {0, 0}; // 起点
pair<int, int> end = {4, 4}; // 终点
vector<pair<int, int>> path = astar(maze, start, end); // 调用astar函数
cout << "Path found:" << endl;
for (auto& p : path) { // 输出路径
cout << "(" << p.first << ", " << p.second << ") ";
}
cout << endl;
return 0;
}CloseList的优化
若地图太大,在后期检查元素是否存在于 CloseList 中是一个很大的开销。
因此采用涂色的方式,新建一个Colored数组,大小与地图相同,如果在CloseList中,则该位置为1,否则为0,需要判断该元素是否存在,取出该值即可
比如检查节点 Node(x = 3, y = 4) 是否在 closed_list 中,先查看二维数组Colored[3,4]的值,如果为1,则表示该节点在 closed_list 中。利用哈希函数可以将二维空间中的坐标(x,y)映射到一维数组的索引上。
这个哈希函数的作用是为每个地图上的节点生成一个唯一的数组索引,以便快速访问和更新 Colored 数组中的状态。通过这种方式,我们可以在常数时间内检查一个节点是否已经在 closed_list 中,即是否已经被访问过。
比如有个5x5的地图,即Map.Size.Y = 5 。我们要检查坐标为(3, 2)的节点是否在 closed_list 中,
使用哈希函数计算出索引 index = 3 * 5 + 2 = 17
查看 Colored[17] 的值。如果 Colored[17] 的值为1,则表示坐标为(3, 2)的节点已经在 closed_list 中;如果为0,则表示该节点不在 closed_list 中。
A*算法的不足
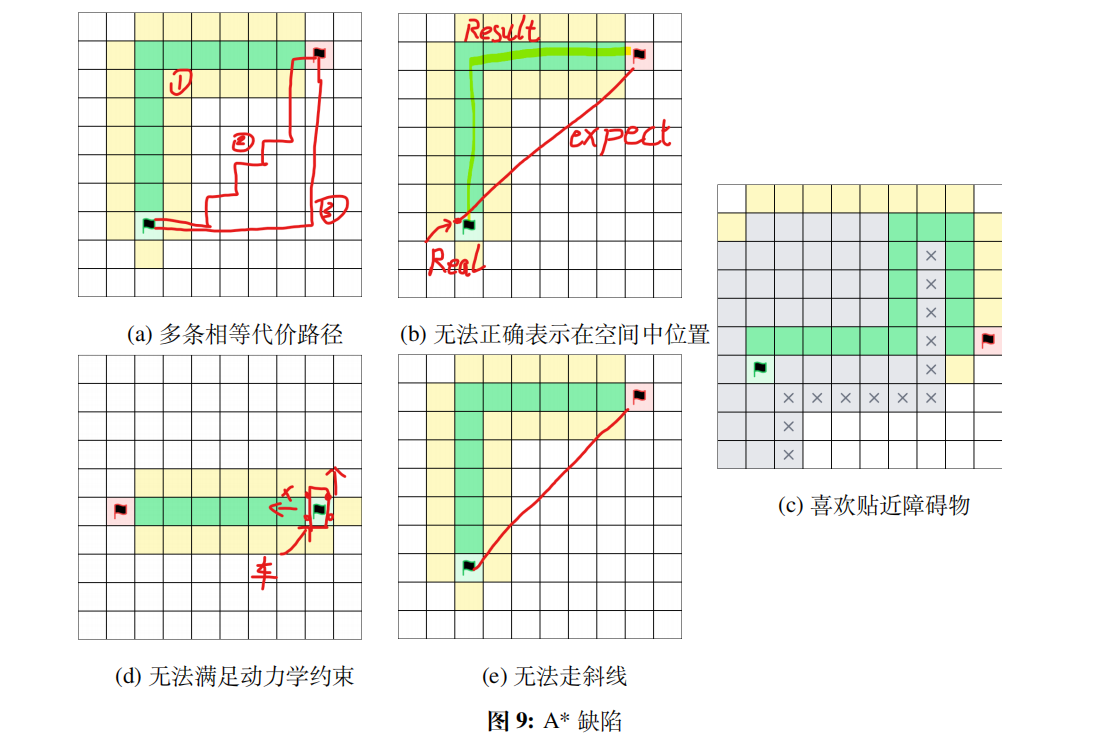
A* 算法的变种 kinodynamic A*
这是一种考虑了动力学约束的寻路方法,可以满足:
一:连续空间的寻路
二:路径点不受到格子限制
三:满足车辆的动力学约束
kinodynamic A*状态空间方程
由于是动力学约束的A*算法,因此需要先解出其 控制量(输入量)U 与 状态量X之间的关系。
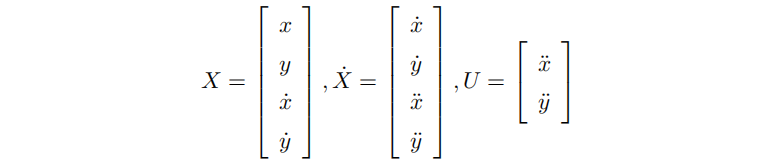
x与y是位置坐标, 与
是速度坐标 ,
与
是加速度坐标
是状态变化率
状态空间方程(用于描述系统状态随时间的变化)如下:
其中 A 是系统矩阵,描述了状态量随时间的权重:
B是输入矩阵,描述输入量如何影响状态变化率的权重
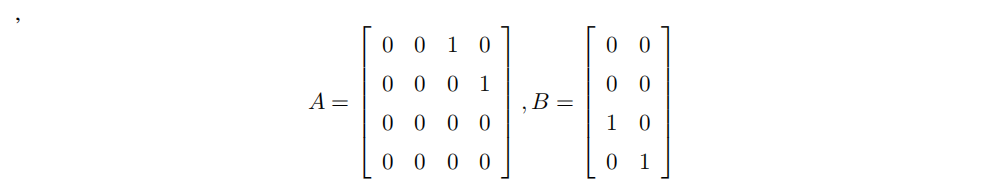
**kinodynamic A***采样方式
kinodynamic A* 在采样上抛弃了网格,每个Node储存的内容为X向量和父节点,通过 获得当前位置不同采样下的
。然后固定一个迭代时间 T,算出生成的状态。
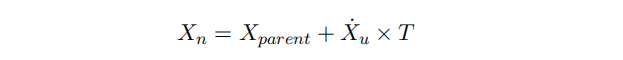
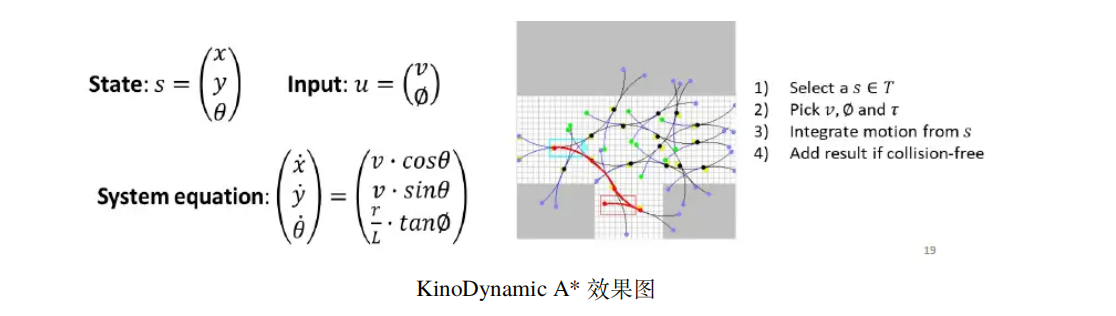
看一下这幅图
状态s中的x和y是位置坐标,θ是朝向角
输入u中的 v 是线速度,是角速度
系统方程描述状态的变化率,其中L是车辆的轴距,是角速度
kinodynamic A*的启发函数h(n)与代价函数g(n)
按照南京理工大学用的是全向轮,所以不关心目标的角度,因此,启发函数使用欧式距离即可。
在 KinoDynamicA*∗*中,代价函数g(n)需要一部分的改变。
从原来的:
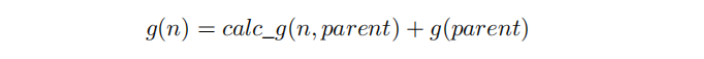
改为
即从父节点 到当前移动到的节点 n的直线距离,比传统A*只能上下左右格子间移动距离好。
Hybrid A*
**聊聊Kinodynamic A***的不足
KinodynamicA ∗ 已经可以做到获得一系列很好的坐标点,但是其采样到的点十分的多,同
一时间会有很多的点在 OpenList 中,这会导致搜索的量变得十分巨大,也就是无法做到快速求
解出结果,常用的在中间计算路径曲线的做法也无法保证达到最好的路径
剪枝策略
在KinodynamicA*的基础上,我们加入网格的限制,即同一个网格只选择一次。这个网格与传统A*的网络相同,但是数据记录的Node保存的是真实坐标的位置,就不是像之前以中心点的坐标
在加入了剪枝策略之后,HybridA∗ 可以以一个较快的速度进行搜索,虽然最后的效果会不如 KinodynamicA∗,但由于后续步骤中的优化器的存在,使得我们在路径规划这一步得出的路径点可以不用那么的完美。

可以看到, HybridA ∗ 在 KinodynamicA ∗ 的基础上 , 对每个网格只保留了一个点,这样可以有效的减少需要搜索的节点数量。
不使用考虑障碍物的启发函数的原因
考虑障碍物的启发函数做法是拓展节点时使用传统A*进行一次近距离的搜索,如果无法得到到达目标点的路径,则看作有障碍,那么启发函数的值就会小的多,这么做可以防止Hybrid A*在死胡同搜索。