本文主要包含:HashMap 插入过程、扩容过程、查询过程和删除过程的源码可视化
1. 操作流程
1.1. 插入过程(put(K key, V value))
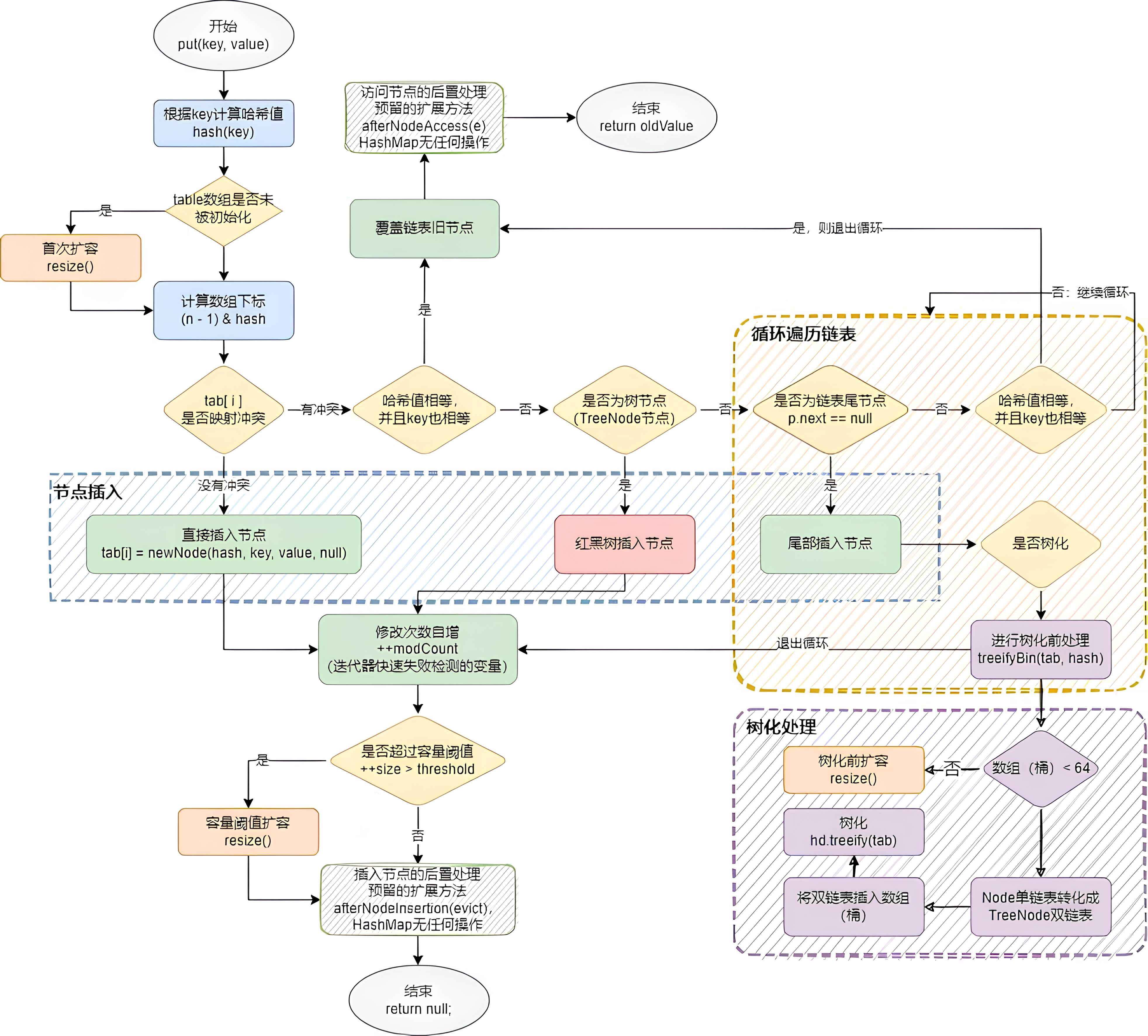
插入流程主要涉及四种操作:扩容(首层扩容和阈值扩容)、单节点插入(无哈希冲突的情况)、链表遍历插入(冲突节点不超8个的情况)、红黑树插入。
插入节点的全流程图:
1.2. 扩容过程(resize())
扩容条件、扩容涉及到的链表挂载、链表树化、树转链表等等,都在前一篇四次扩容的文章中讲到,渐进式的学习HashMap扩容。
HashMap扩容源码可视化
文章链接:https://mp.weixin.qq.com/s/J3kU51hb-GcM4Rsp7QCIFw
视频链接:https://www.bilibili.com/video/BV1wM3KzaE3d/
1.3. 查询过程(get(Object key))
-
空表或
key == null:立即返回null(nullkey 存储在索引 0)。 -
计算
hash、下标i -
遍历
-
如果
table[i]为单链表,逐节点比较hash与key.equals; -
如果为红黑树,调用
TreeNode的getTreeNode,按树结构快速查找(对数复杂度)。
-
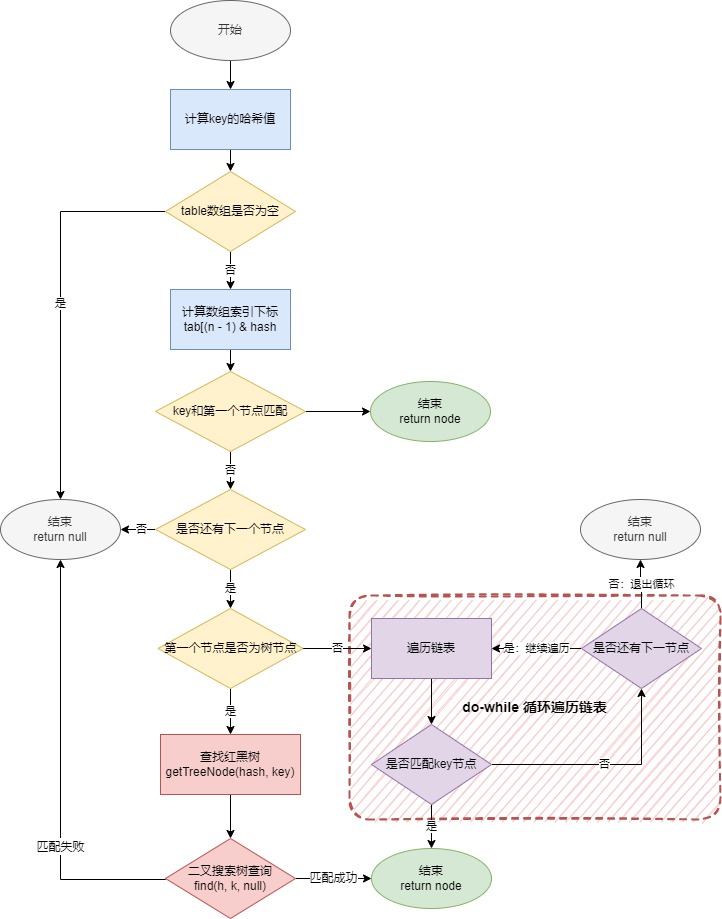
查找元素全流程图:
1.4. 删除过程(remove(Object key))
最后将展示单链表的节点删除和红黑树节点的删除可视化过程。
-
计算
hash、下标i。 -
定位到槽位的链表或树,找到目标节点。
-
单链表:直接断链跳过;红黑树:调用
removeTreeNode完成删除。 -
size--,更新modCount,返回被删节点的值。
删除链表节点
跟普通链表删除节点一样简单,下面直接通过动图来理解
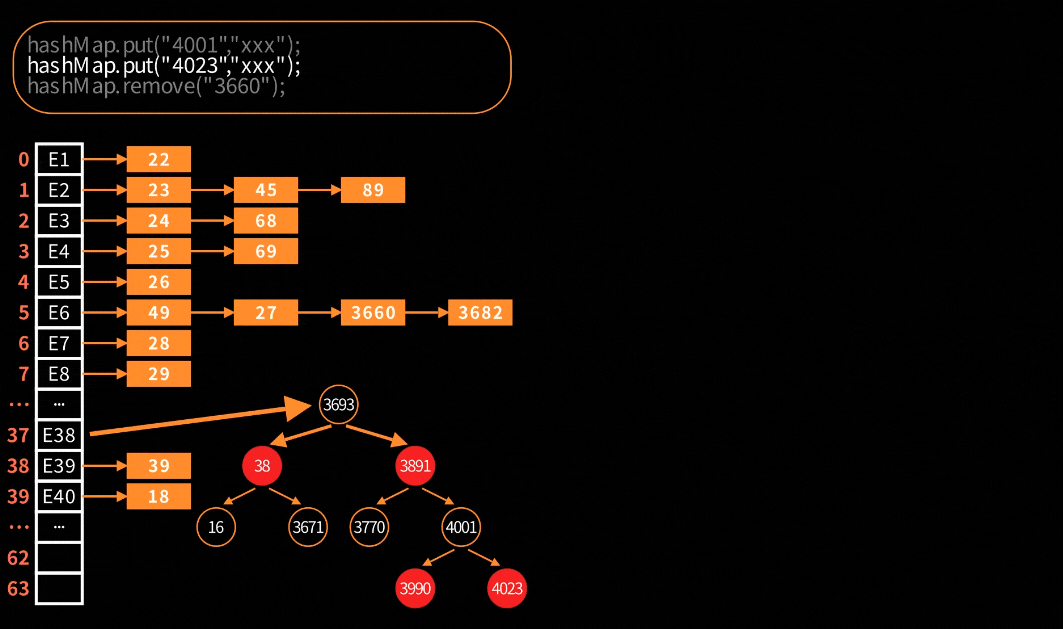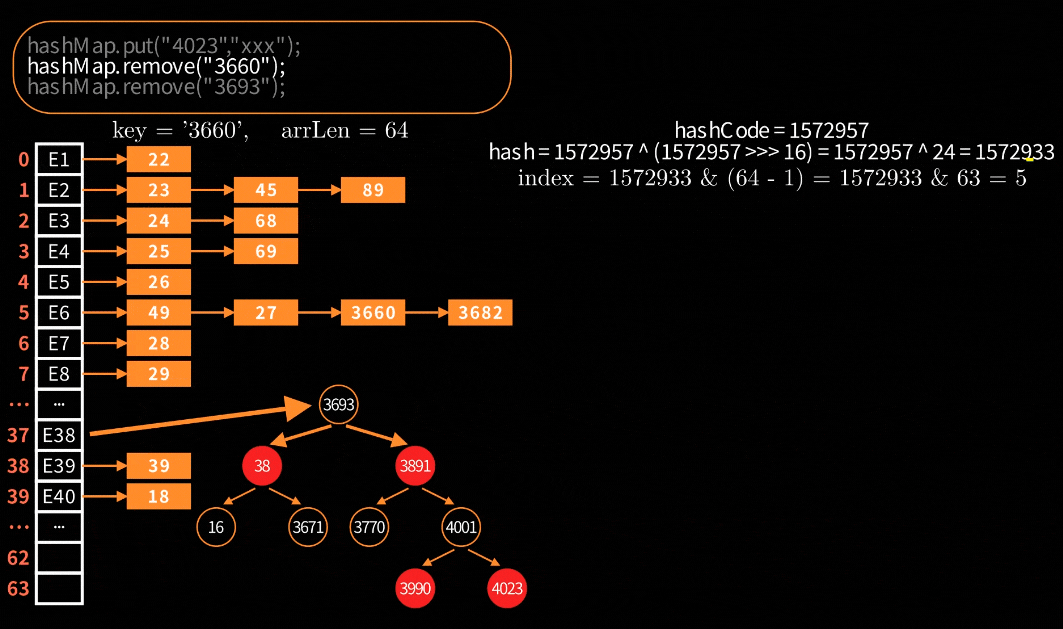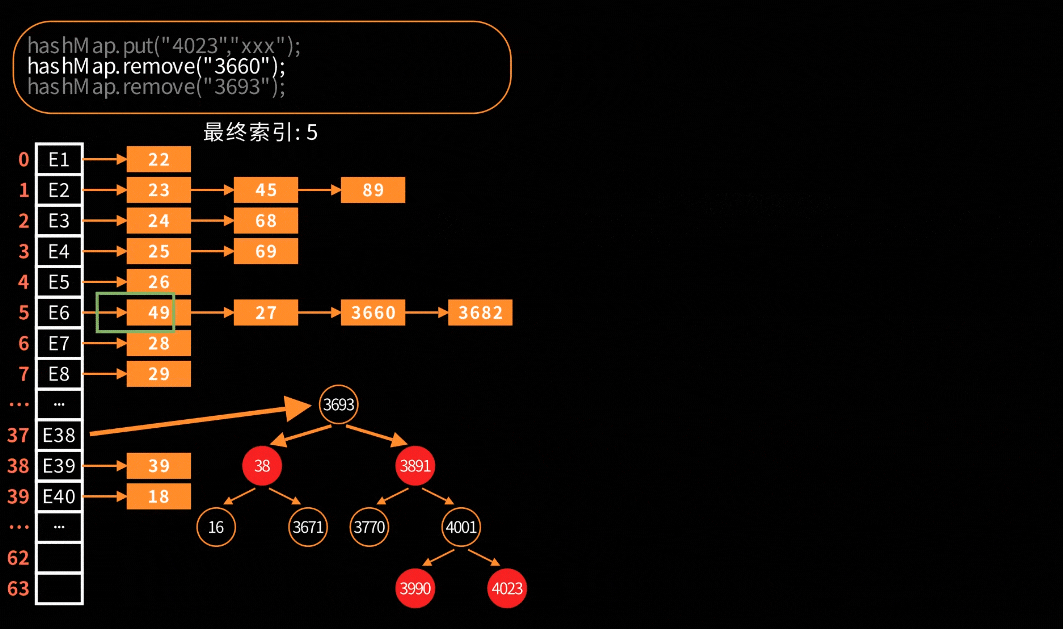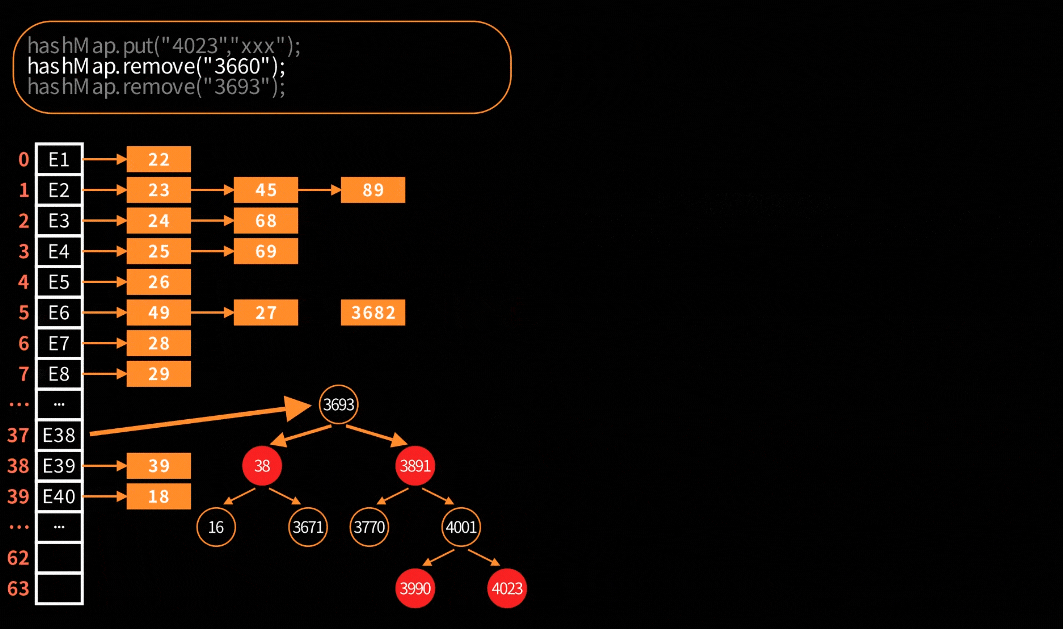
删除红黑树节点
对于链表的删除处理是很简单很好理解,但是对于红黑树的删除就会比较复杂。在HashMap中,红黑树节点删除的可视化:
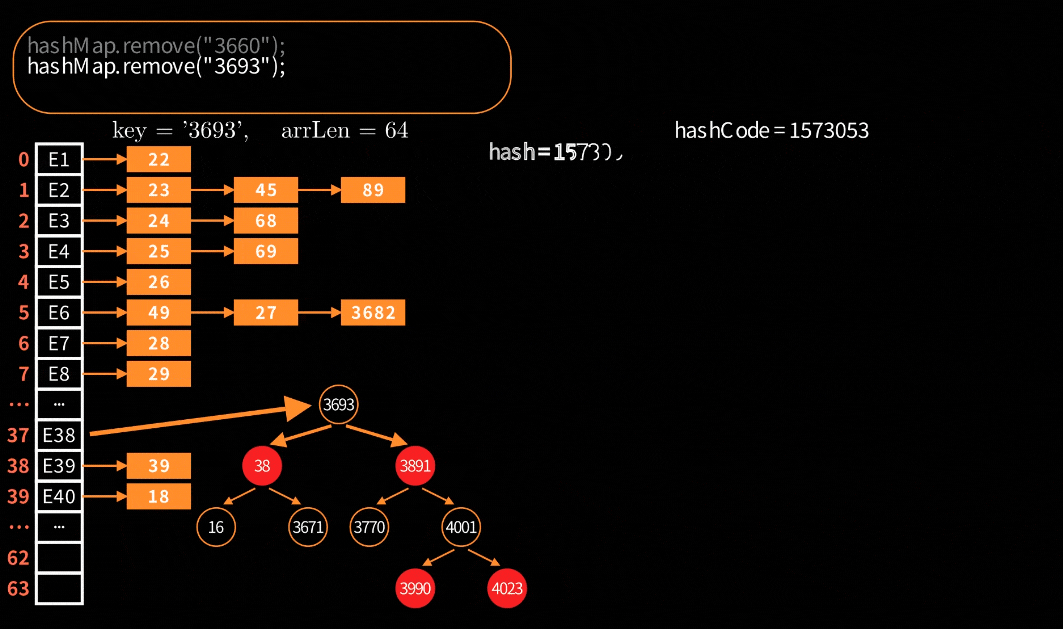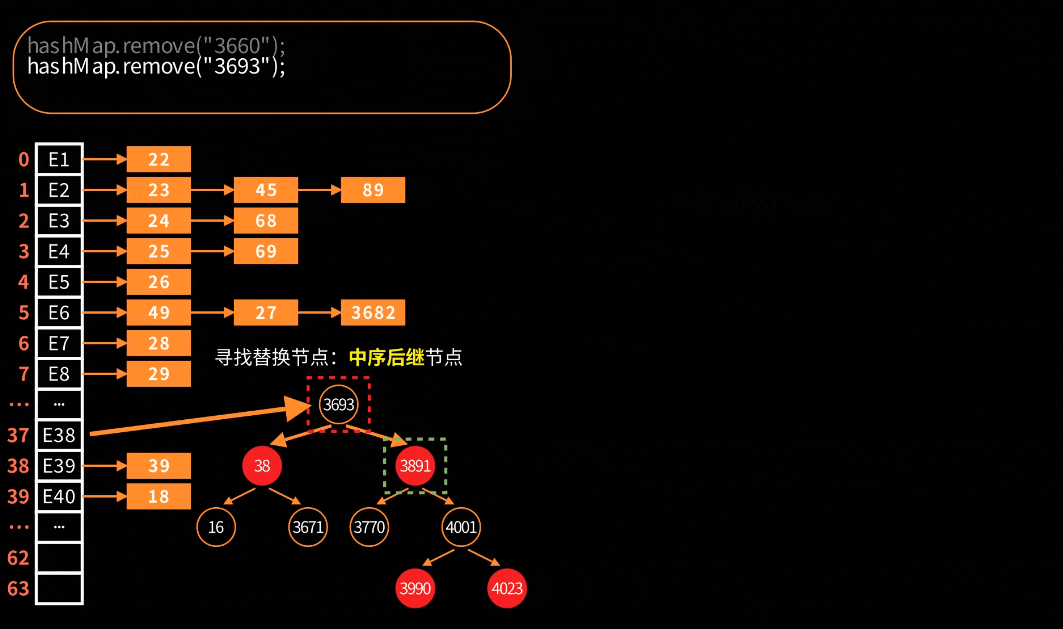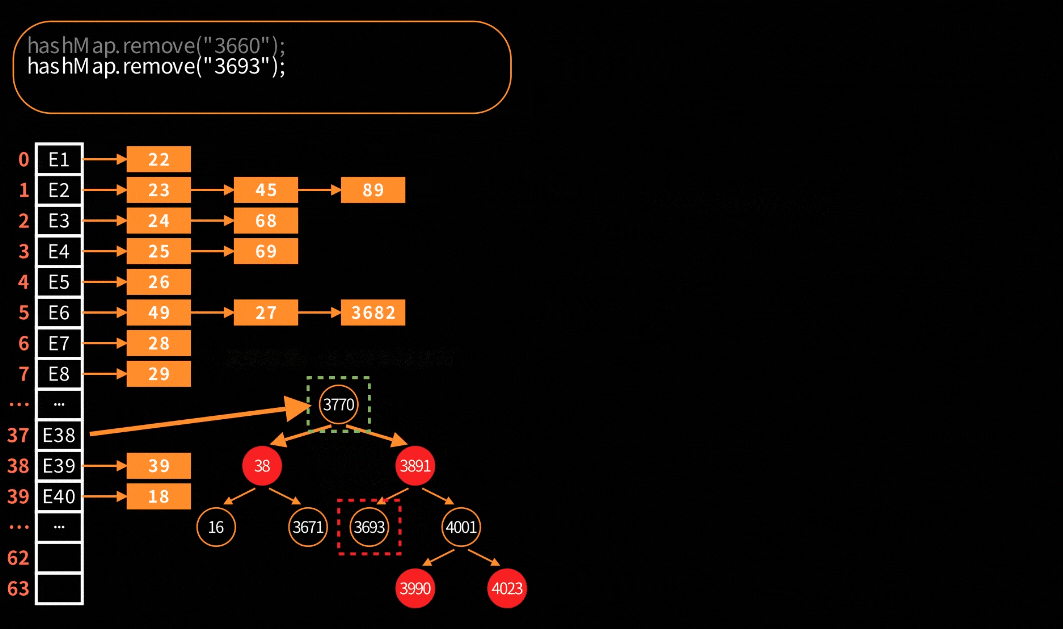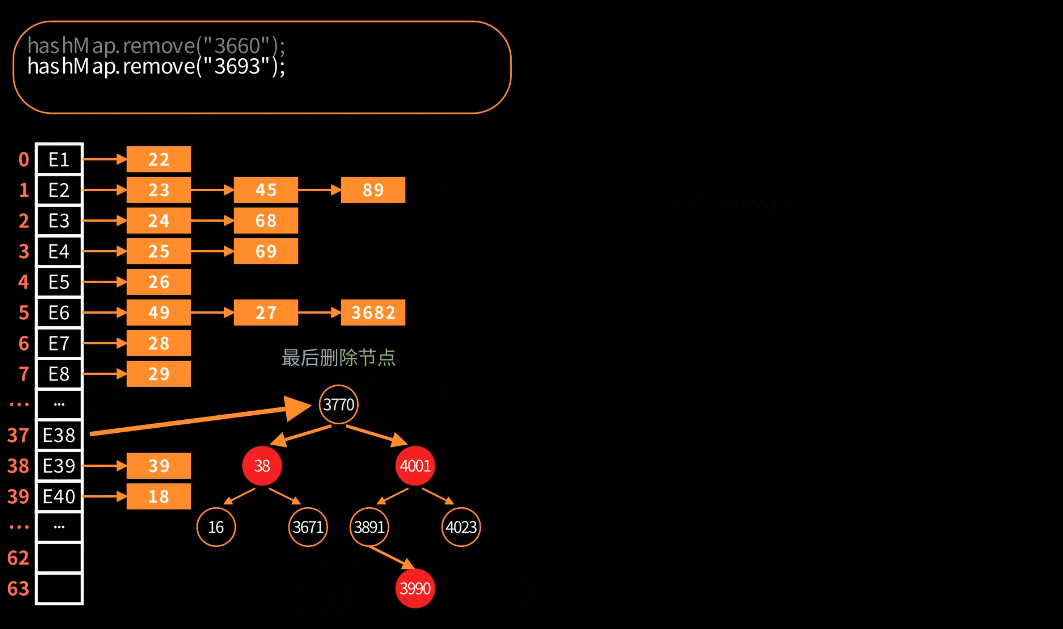
关键步骤大致分为四步:寻找替换节点、进入待删除状态、红黑树平衡调整和最终删除节点。
最主要的两步源码如下,其次就是红黑树数据结构删除过程的理解:
寻找替换:寻找中序后继节点作为替换节点。比如:红黑树左中右序为1、2、3、4,删除了2节点,那么就找3节点作为替换节点;如果删除3节点,那么就找4节点作为替换。对应的源代码如下
java
if (pl != null && pr != null) {
// 如果左右都不为空,找中序的后继节点替换,(右子树最靠左的节点)
TreeNode<K,V> s = pr, sl;
while ((sl = s.left) != null)
s = sl;
...
}删除黑节点树平衡:
删除的主要源码如下,已为每一行源码附上注释。
java
// map: 当前所在的 HashMap 实例
// tab: 哈希表数组(即 table)
// movable=true
final void removeTreeNode(HashMap<K,V> map, Node<K,V>[] tab,
boolean movable) {
int n;
// 如果表为 null 或长度为 0,直接返回(无操作)
if (tab == null || (n = tab.length) == 0)
return;
// 用哈希值定位当前节点所在的桶 index
int index = (n - 1) & hash;
// 获取根节点
TreeNode<K,V> first = (TreeNode<K,V>)tab[index], root = first, rl;
// 从链表中断开当前节点(this),红黑树同时是双向链表这点必须知道,所以才有维护链表的操作
TreeNode<K,V> succ = (TreeNode<K,V>)next, pred = prev;
if (pred == null)
tab[index] = first = succ;
else
pred.next = succ;
if (succ != null)
succ.prev = pred;
// 如果断链后没有剩余节点(即只有当前一个节点),直接返回
if (first == null)
return;
if (root.parent != null)
root = root.root();
if (root == null
|| (movable
&& (root.right == null
|| (rl = root.left) == null
|| rl.left == null))) {
tab[index] = first.untreeify(map); // too small
return;
}
// 红黑树删除操作
TreeNode<K,V> p = this, pl = left, pr = right, replacement;
// 处理删除节点p 同时有左右子节点的情况
if (pl != null && pr != null) {
// 如果左右都不为空,找中序的后继替换,(右子树最靠左的节点)
TreeNode<K,V> s = pr, sl;
while ((sl = s.left) != null) // find successor
s = sl;
// 节点颜色交换
boolean c = s.red; s.red = p.red; p.red = c; // swap colors
// 交换结构:把后继节点换上来
TreeNode<K,V> sr = s.right;
TreeNode<K,V> pp = p.parent;
// p 是 s 的直接父节点
if (s == pr) {
p.parent = s;
s.right = p;
}
else {
TreeNode<K,V> sp = s.parent;
if ((p.parent = sp) != null) {
if (s == sp.left)
sp.left = p;
else
sp.right = p;
}
if ((s.right = pr) != null)
pr.parent = s;
}
// 调整左子树与父指针:p 的左右清空(它即将被删),s 左右指针都设置好(接替 p)
p.left = null;
if ((p.right = sr) != null)
sr.parent = p;
if ((s.left = pl) != null)
pl.parent = s;
// s 接替 p 成为新的 root 的子节点
if ((s.parent = pp) == null)
root = s;
else if (p == pp.left)
pp.left = s;
else
pp.right = s;
// 设置替换节点
if (sr != null)
replacement = sr;
else
replacement = p;
}
// 处理删除节点p 有一个或没有子节点情况
else if (pl != null)
replacement = pl;
else if (pr != null)
replacement = pr;
else
replacement = p;
// 让 replacement 替换掉 删除节点p 的位置
if (replacement != p) {
TreeNode<K,V> pp = replacement.parent = p.parent;
if (pp == null)
root = replacement;
else if (p == pp.left)
pp.left = replacement;
else
pp.right = replacement;
p.left = p.right = p.parent = null;
}
// 如果删除节点p 是黑节点,需要平衡红黑树
TreeNode<K,V> r = p.red ? root : balanceDeletion(root, replacement);
// 如果 p 等于 replacement,说明删除的节点是叶子节点,断开叶子节点
if (replacement == p) {
TreeNode<K,V> pp = p.parent;
p.parent = null;
if (pp != null) {
if (p == pp.left)
pp.left = null;
else if (p == pp.right)
pp.right = null;
}
}
// 将新的 root 移动到链表最前(优化访问)
if (movable)
moveRootToFront(tab, r);
}2. 性能与并发考虑
时间复杂度
| 操作 | 平均时间复杂度 | 最坏时间复杂度 | 备注 |
|---|---|---|---|
get |
O(1) | O(log n) | 红黑树查找最坏 O(log n) |
put |
O(1) | O(log n) | 链表树化后插树最坏 O(log n) |
remove |
O(1) | O(log n) | 红黑树删除维护平衡 O(log n) |
resize |
O(1) | O(n) | 摊销成本后每次插入 O(1) |
| 遍历全部元素 | O(n) | O(n) |
并发风险
HashMap 非线程安全,在多线程无外部同步时可能出现数据丢失或死循环(扩容时环路)。
多线程并发场景推荐使用 ConcurrentHashMap,或者对 HashMap 外层加锁(如 Collections.synchronizedMap,串行效率低)
3. 在 HashMap 中红黑树同时是双向链表?
链表节点(未树化) :Node<K,V> 类型,只包含:
java
Node<K,V> {
final int hash;
final K key;
V value;
Node<K,V> next;
}✅ 是 单向链表。
树化节点(TreeNode) :扩展自 Node<K,V>,添加了:
java
TreeNode<K,V> extends Node<K,V> {
TreeNode<K,V> parent;
TreeNode<K,V> left;
TreeNode<K,V> right;
TreeNode<K,V> prev; // 🔥 这是额外的双向链表字段
boolean red;
}✅ 是 双向链表 + 红黑树结构。
3.1. 红黑树根节点始终是双向链表的头节点
这里所说的双向链表结构指的是:在同一个桶中的红黑树。
在不同的桶中,红黑树之间是没有联系的,也不存在双向链表。
moveRootToFront 这个方法有两个作用
-
更新数组桶指向新的根节点
-
更新根节点为双向链表的头节点,并将旧的根节点作为下一节点接上(就是新的根节点和旧的根节点互换位置)
java
static <K,V> void moveRootToFront(Node<K,V>[] tab, TreeNode<K,V> root) {
int n;
if (root != null && tab != null && (n = tab.length) > 0) {
int index = (n - 1) & root.hash;
// 获取旧的根节点
TreeNode<K,V> first = (TreeNode<K,V>)tab[index];
if (root != first) {
Node<K,V> rn;
// 数组桶指向新的根节点
tab[index] = root;
// 断开 root 在原链表中的连接:先取出root上一节点
TreeNode<K,V> rp = root.prev;
// 再将前后节点连接起来,从而断开root 在原链表中的连接
if ((rn = root.next) != null)
((TreeNode<K,V>)rn).prev = rp;
if (rp != null)
rp.next = rn;
// 新的根节点调整为头节点
if (first != null)
first.prev = root;
// 旧的根节点成为头节点的下一节点
root.next = first;
root.prev = null;
}
assert checkInvariants(root);
}
}总的来说,没什么深奥的,就是单链表和双链表的作用区别,为了任意树节点都可以更快的找到上一节点,提高操作效率。
4. 总结
HashMap插入流程、扩容流程、查询流程,以及删除节点时链表和红黑树的处理。对 HashMap 会有一个基本而完整的理解。接下来可以深入学习红黑树数据结构,这是学习HashMap、LinkedHashMap、TreeMap等集合必须掌握的数据结构。

Java集合--HashMap底层原理可视化,秒懂扩容、链化、树化
查看往期设计模式文章的:设计模式
原创不易,觉得还不错的,三连支持:点赞、分享、推荐↓