1. 多项式环(Polynomial Rings)
设 f ∈ Z [ x ] f \in \mathbb{Z}[x] f∈Z[x] 是首一多项式(最高次项系数为1)
则环 R = Z [ x ] / ( f ) R = \mathbb{Z}[x]/(f) R=Z[x]/(f)
元素为:所有次数 < deg ( f ) < \deg(f) <deg(f) 的多项式。
运算规则:
- 加法:逐系数模整数加法。
- 乘法:计算多项式乘积后模 f ( x ) f(x) f(x) 取余(余式次数 < deg ( f ) < \deg(f) <deg(f))。
多项式的向量表示:
多项式 a ( x ) = ∑ i = 0 n − 1 a i x i a(x) = \sum\limits_{i=0}^{n-1} a_i x^i a(x)=i=0∑n−1aixi 对应系数向量 a = ( a 0 , a 1 , ... , a n − 1 ) ∈ Z n \boldsymbol{a} = (a_0, a_1, \dots, a_{n-1}) \in \mathbb{Z}^n a=(a0,a1,...,an−1)∈Zn。
例如:
R = Z [ x ] / ( x 4 + 2 x 2 − 11 x + 1 ) R = \mathbb{Z}[x]/(x^4 + 2x^2 -11x +1) R=Z[x]/(x4+2x2−11x+1) 中,
a ( x ) = 23 + 11 x 2 + 7 x 3 ↔ ( 23 , 0 , 11 , 7 ) a(x) = 23 + 11x^2 + 7x^3 \leftrightarrow (23, 0, 11, 7) a(x)=23+11x2+7x3↔(23,0,11,7).
2. 理想格(Ideal Lattices)
理想:
全称:理想子环
定义: ( R , + , . ) (R,+,.) (R,+,.)是环, I I I是 R R R的非空子集。如果 ( I , + , . ) (I,+,.) (I,+,.)满足以下条件:
- 加法子群: ( I , + ) (I,+) (I,+)是 ( R , + ) (R,+) (R,+)的子群
- 乘法吸收律: ∀ r ∈ R , ∀ a ∈ I ⇒ r a ∈ I ( a r ∈ I ) \forall r\in R,\forall a \in I\Rightarrow ra\in I(ar\in I) ∀r∈R,∀a∈I⇒ra∈I(ar∈I)
则称 I I I是 R R R的左(右)理想。
理想的判断:
(R,+,.)是环,I是R的左(右)理想,
∀ a , b ∈ I , ∀ r ∈ R \forall a,b \in I ,\forall r \in R ∀a,b∈I,∀r∈R当且仅当, I I I满足以下条件:
- 加法子群: ( I , + ) (I,+) (I,+)是 ( R , + ) (R,+) (R,+)的子群(加法封闭性: a + b ∈ I a+b \in I a+b∈I加法逆元: − a ∈ I -a \in I −a∈I)
- 乘法吸收律: r a ∈ I ( a r ∈ I ) ra \in I(ar \in I) ra∈I(ar∈I)

理想三巨头:



主理想 :由单个多项式生成 ⟨ a ( x ) ⟩ = { a ( x ) r ( x ) m o d f ∣ r ∈ R } \langle a(x) \rangle = \{ a(x) r(x) \mod f \mid r \in R \} ⟨a(x)⟩={a(x)r(x)modf∣r∈R}。 ( 环 R = Z [ x ] / ( f ) R = \mathbb{Z}[x]/(f) R=Z[x]/(f) )
理想格 :
理想 I I I 中所有多项式系数向量构成的整数格 L ( I ) ⊂ R n L(I) \subset \mathbb{R}^n L(I)⊂Rn。(理想本身就满足群的性质)
本篇仅考虑 f ( x ) = x n − 1 f(x) = x^n - 1 f(x)=xn−1(循环格)或 f ( x ) = x n + 1 f(x) = x^n + 1 f(x)=xn+1(反循环格)。
3. 循环格与反循环格(结构化的格)
(1)循环格
循环格最早在2002年被Micciancio研究
定义:
设 L ⊆ Z n L \subseteq \mathbb{Z}^n L⊆Zn 是一个格。若对任意向量 v = ( v 0 , v 1 , ... , v n − 1 ) ∈ L \boldsymbol{v} = (v_0, v_1, \dots, v_{n-1}) \in L v=(v0,v1,...,vn−1)∈L,其左循环移位 ( v n − 1 , v 0 , v 1 , ... , v n − 2 ) ∈ L (v_{n-1}, v_0, v_1, \dots, v_{n-2}) \in L (vn−1,v0,v1,...,vn−2)∈L,则 L L L 称为循环格。
定理:
R = Z [ x ] / ( x n − 1 ) R=\mathbb{Z}[x]/(x^n-1) R=Z[x]/(xn−1),则其每一个理想格都是循环格。
ps理想与格关系:每个理想都对应一个格(理想定义天然包含离散子群的条件)
主理想中的多项式通过系数提取转化为向量,这些向量的全体构成一个格。
对 R = Z [ x ] / ( x n − 1 ) R = \mathbb{Z}[x]/(x^n - 1) R=Z[x]/(xn−1) 的主理想 I I I= ⟨ a ( x ) ⟩ \langle a(x) \rangle ⟨a(x)⟩, I = { a ( x ) ⋅ r ( x ) m o d ( x n − 1 ) ∣ r ( x ) ∈ R } I = \left\{ a(x) \cdot r(x) \bmod (x^n - 1) \mid r(x) \in R \right\} I={a(x)⋅r(x)mod(xn−1)∣r(x)∈R}
则其对应的格 ( L ( I ) L(I) L(I) ) 定义为: L ( I ) = { 系数向量 ∣ p ( x ) ∈ I } = { s ∈ Z n ∣ s = A r , r ∈ Z n } L(I) = \{\text{系数向量} \mid p(x) \in I\} = \{\boldsymbol{s} \in \mathbb{Z}^n \mid \boldsymbol{s} = \boldsymbol{A}\boldsymbol{r},\ \boldsymbol{r} \in \mathbb{Z}^n\} L(I)={系数向量∣p(x)∈I}={s∈Zn∣s=Ar, r∈Zn} 其中 ( A \boldsymbol{A} A) 是循环矩阵。
注:(乘积 s ( x ) = a ( x ) ⋅ r ( x ) m o d ( x n − 1 ) s(x) = a(x) \cdot r(x) \bmod (x^n - 1) s(x)=a(x)⋅r(x)mod(xn−1) 的系数向量 s \boldsymbol{s} s 由循环卷积给出: s k = ∑ i + j ≡ k ( m o d n ) a i r j s_k = \sum\limits_{\substack{i+j \equiv k \pmod{n}}} a_i r_j sk=i+j≡k(modn)∑airj 这等价于矩阵乘法 s = A r \boldsymbol{s} = \boldsymbol{A}\boldsymbol{r} s=Ar。)
关键理解
设 a ( x ) = a 0 + a 1 x + ⋯ + a n − 1 x n − 1 a(x) = a_0 + a_1 x + \cdots + a_{n-1} x^{n-1} a(x)=a0+a1x+⋯+an−1xn−1,其系数向量为 a = ( a 0 , a 1 , ... , a n − 1 ) ⊤ \boldsymbol{a} = (a_0, a_1, \ldots, a_{n-1})^\top a=(a0,a1,...,an−1)⊤。
理想 I I I 是 z − \mathbb{z}- z−模的生成元是集合 { a ( x ) , x a ( x ) , x 2 a ( x ) , ... , x n − 1 a ( x ) } \{ a(x), x a(x), x^2 a(x), \ldots, x^{n-1} a(x) \} {a(x),xa(x),x2a(x),...,xn−1a(x)}。
因为:
将 r ( x ) r(x) r(x) 代入 I I I 中元素的表达式,得: a ( x ) ⋅ r ( x ) = a ( x ) ⋅ ( r 0 + r 1 x + ⋯ + r n − 1 x n − 1 ) = r 0 ⋅ a ( x ) + r 1 ⋅ ( x a ( x ) ) + ⋯ + r n − 1 ⋅ ( x n − 1 a ( x ) ) a(x) \cdot r(x) = a(x) \cdot \left( r_0 + r_1 x + \cdots + r_{n-1} x^{n-1} \right) = r_0 \cdot a(x) + r_1 \cdot \left( x a(x) \right) + \cdots + r_{n-1} \cdot \left( x^{n-1} a(x) \right) a(x)⋅r(x)=a(x)⋅(r0+r1x+⋯+rn−1xn−1)=r0⋅a(x)+r1⋅(xa(x))+⋯+rn−1⋅(xn−1a(x)) 这说明: I I I 中任意元素都是 { a ( x ) , x a ( x ) , ... , x n − 1 a ( x ) } \{ a(x), x a(x), \ldots, x^{n-1} a(x) \} {a(x),xa(x),...,xn−1a(x)} 的 整数线性组合 (系数 r i ∈ Z r_i \in \mathbb{Z} ri∈Z)。
即集合 { a ( x ) , x a ( x ) , x 2 a ( x ) , ... , x n − 1 a ( x ) } \{ a(x), xa(x), x^2a(x), \dots, x^{n-1}a(x) \} {a(x),xa(x),x2a(x),...,xn−1a(x)} 的系数向量张成格 L ( I ) L(I) L(I),其矩阵形式为循环矩阵.
A = circ ( a ) = [ a 0 a n − 1 ⋯ a 1 a 1 a 0 ⋯ a 2 ⋮ ⋮ ⋱ ⋮ a n − 1 a n − 2 ⋯ a 0 ] \boldsymbol{A} = \text{circ}(\boldsymbol{a}) = \begin{bmatrix} a_0 & a_{n-1} & \cdots & a_1 \\ a_1 & a_0 & \cdots & a_2 \\ \vdots & \vdots & \ddots & \vdots \\ a_{n-1} & a_{n-2} & \cdots & a_0 \end{bmatrix} A=circ(a)= a0a1⋮an−1an−1a0⋮an−2⋯⋯⋱⋯a1a2⋮a0
A可逆条件 : gcd ( a ( x ) , x n − 1 ) = 1 \gcd(a(x), x^n - 1) = 1 gcd(a(x),xn−1)=1(在 Q \mathbb{Q} Q 上)。
记作: A = circ ( a ) \boldsymbol{A} = \text{circ}(\boldsymbol{a}) A=circ(a)
(2) 反循环格
定义:
设 L ⊆ Z n L \subseteq \mathbb{Z}^n L⊆Zn 是一个格。若对任意向量 v = ( v 0 , v 1 , ... , v n − 1 ) ∈ L \boldsymbol{v} = (v_0, v_1, \dots, v_{n-1}) \in L v=(v0,v1,...,vn−1)∈L,其反循环移位 ( − v n − 1 , v 0 , v 1 , ... , v n − 2 ) ∈ L (-v_{n-1}, v_0, v_1, \dots, v_{n-2}) \in L (−vn−1,v0,v1,...,vn−2)∈L,则 L L L 称为反循环格。
定理:
设 R = Z [ x ] / ( x n + 1 ) R = \mathbb{Z}[x]/(x^n + 1) R=Z[x]/(xn+1),则其每一个理想格都是反循环格。
ps 理想与格关系:每个理想都对应一个格(理想定义天然包含离散子群的条件)。
主理想中的多项式通过系数提取转化为向量,这些向量的全体构成一个格。
主理想对应的格
对 R = Z [ x ] / ( x n + 1 ) R = \mathbb{Z}[x]/(x^n + 1) R=Z[x]/(xn+1) 的主理想 I = ⟨ a ( x ) ⟩ I = \langle a(x) \rangle I=⟨a(x)⟩,
I = { a ( x ) ⋅ r ( x ) m o d ( x n + 1 ) ∣ r ( x ) ∈ R } I = \left\{ a(x) \cdot r(x) \bmod (x^n + 1) \mid r(x) \in R \right\} I={a(x)⋅r(x)mod(xn+1)∣r(x)∈R}
则其对应的格 L ( I ) L(I) L(I) 定义为:
L ( I ) = { 系数向量 ∣ p ( x ) ∈ I } = { s ∈ Z n ∣ s = B r , r ∈ Z n } L(I) = \{\text{系数向量} \mid p(x) \in I\} = \{\boldsymbol{s} \in \mathbb{Z}^n \mid \boldsymbol{s} = \boldsymbol{B}\boldsymbol{r},\ \boldsymbol{r} \in \mathbb{Z}^n\} L(I)={系数向量∣p(x)∈I}={s∈Zn∣s=Br, r∈Zn}
其中 B \boldsymbol{B} B 是反循环矩阵。
注:(乘积 s ( x ) = a ( x ) ⋅ r ( x ) m o d ( x n + 1 ) s(x) = a(x) \cdot r(x) \bmod (x^n + 1) s(x)=a(x)⋅r(x)mod(xn+1) 的系数向量 s \boldsymbol{s} s 由反循环卷积 给出:
s k = ∑ i + j ≡ k ( m o d n ) i + j < n a i r j − ∑ i + j ≡ k + n ( m o d n ) i + j ≥ n a i r j s_k = \sum_{\substack{i + j \equiv k \pmod{n} \\ i + j < n}} a_i r_j - \sum_{\substack{i + j \equiv k + n \pmod{n} \\ i + j \geq n}} a_i r_j sk=∑i+j≡k(modn)i+j<nairj−∑i+j≡k+n(modn)i+j≥nairj
这等价于矩阵乘法 s = B r \boldsymbol{s} = \boldsymbol{B}\boldsymbol{r} s=Br。
关键理解
设 a ( x ) = a 0 + a 1 x + ⋯ + a n − 1 x n − 1 a(x) = a_0 + a_1 x + \cdots + a_{n-1} x^{n-1} a(x)=a0+a1x+⋯+an−1xn−1,其系数向量为 a = ( a 0 , a 1 , ... , a n − 1 ) ⊤ \boldsymbol{a} = (a_0, a_1, \ldots, a_{n-1})^\top a=(a0,a1,...,an−1)⊤。
理想 I I I 作为 Z \mathbb{Z} Z-模的生成元是集合 { a ( x ) , x a ( x ) , x 2 a ( x ) , ... , x n − 1 a ( x ) } \{ a(x), x a(x), x^2 a(x), \ldots, x^{n-1} a(x) \} {a(x),xa(x),x2a(x),...,xn−1a(x)}。
因为:
将 r ( x ) r(x) r(x) 代入 I I I 中元素的表达式,得:
a ( x ) ⋅ r ( x ) = a ( x ) ⋅ ( r 0 + r 1 x + ⋯ + r n − 1 x n − 1 ) = r 0 ⋅ a ( x ) + r 1 ⋅ ( x a ( x ) ) + ⋯ + r n − 1 ⋅ ( x n − 1 a ( x ) ) a(x) \cdot r(x) = a(x) \cdot \left( r_0 + r_1 x + \cdots + r_{n-1} x^{n-1} \right) = r_0 \cdot a(x) + r_1 \cdot \left( x a(x) \right) + \cdots + r_{n-1} \cdot \left( x^{n-1} a(x) \right) a(x)⋅r(x)=a(x)⋅(r0+r1x+⋯+rn−1xn−1)=r0⋅a(x)+r1⋅(xa(x))+⋯+rn−1⋅(xn−1a(x))
这说明: I I I 中任意元素都是 { a ( x ) , x a ( x ) , ... , x n − 1 a ( x ) } \{ a(x), x a(x), \ldots, x^{n-1} a(x) \} {a(x),xa(x),...,xn−1a(x)} 的整数线性组合 (系数 r i ∈ Z r_i \in \mathbb{Z} ri∈Z)。
即集合 { a ( x ) , x a ( x ) , x 2 a ( x ) , ... , x n − 1 a ( x ) } \{ a(x), x a(x), x^2 a(x), \dots, x^{n-1} a(x) \} {a(x),xa(x),x2a(x),...,xn−1a(x)} 的系数向量张成格 L ( I ) L(I) L(I),其矩阵形式为反循环矩阵:
B = circ ‾ ( a ) = [ a 0 − a n − 1 − a n − 2 ⋯ − a 1 a 1 a 0 − a n − 1 ⋯ − a 2 a 2 a 1 a 0 ⋯ − a 3 ⋮ ⋮ ⋮ ⋱ ⋮ a n − 1 a n − 2 a n − 3 ⋯ a 0 ] \boldsymbol{B} = \overline{\text{circ}}(\boldsymbol{a}) = \begin{bmatrix} a_0 & -a_{n-1} & -a_{n-2} & \cdots & -a_1 \\ a_1 & a_0 & -a_{n-1} & \cdots & -a_2 \\ a_2 & a_1 & a_0 & \cdots & -a_3 \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ a_{n-1} & a_{n-2} & a_{n-3} & \cdots & a_0 \end{bmatrix} B=circ(a)= a0a1a2⋮an−1−an−1a0a1⋮an−2−an−2−an−1a0⋮an−3⋯⋯⋯⋱⋯−a1−a2−a3⋮a0
B \boldsymbol{B} B 可逆条件 : gcd ( a ( x ) , x n + 1 ) = 1 \gcd(a(x), x^n + 1) = 1 gcd(a(x),xn+1)=1(在 Q \mathbb{Q} Q 上)。
记作 B = circ ‾ ( a ) \boldsymbol{B} = \overline{\text{circ}}(\boldsymbol{a}) B=circ(a)
密码学意义对比
| 特性 | 循环格 | 反循环格 |
|---|---|---|
| 多项式环 | Z [ x ] / ( x n − 1 ) \mathbb{Z}[x]/(x^n - 1) Z[x]/(xn−1) | Z [ x ] / ( x n + 1 ) \mathbb{Z}[x]/(x^n + 1) Z[x]/(xn+1) |
| 安全强度 | 较低( x n − 1 x^n-1 xn−1 可因式分解) | 较高( x n + 1 x^n+1 xn+1 不可约) |
| 移位操作 | ( v n − 1 , v 0 , ... , v n − 2 ) (v_{n-1}, v_0, \dots, v_{n-2}) (vn−1,v0,...,vn−2) | ( − v n − 1 , v 0 , ... , v n − 2 ) (-v_{n-1}, v_0, \dots, v_{n-2}) (−vn−1,v0,...,vn−2) |
| 应用场景 | 早期方案(Micciancio 2002) | 后量子密码标准(Kyber, Dilithium) |
注 :反循环格在现代密码学中更常用,因 x n + 1 x^n + 1 xn+1 在 n = 2 w n=2^w n=2w 时不可约,提供更强的安全性保证。
4. Ring-SIS
2006年由Micciancio和Rosen提出
Ring-SIS ( n , ℓ , q , B ) (n,\ell,q,B) (n,ℓ,q,B)安全参数 n n n(通常为2的幂),模数 q q q,目标向量数量 ℓ \ell ℓ,范数界 B B B
定义
给定 a 1 , ... , a ℓ ∈ R q = Z q [ x ] / ( x n + 1 ) a_1, \dots, a_\ell \in R_q = \mathbb{Z}q[x]/(x^n + 1) a1,...,aℓ∈Rq=Zq[x]/(xn+1)。找到非零 z 1 , ... , z ℓ ∈ R q z_1, \dots, z\ell \in R_q z1,...,zℓ∈Rq,使得(多项式卷积相乘)
∑ i = 1 ℓ a i z i = 0 ( m o d q ) , ∥ z i ∥ ∞ ≤ B . \sum_{i=1}^\ell a_i z_i = 0 \pmod{q}, \quad \|z_i\|\infty \leq B. i=1∑ℓaizi=0(modq),∥zi∥∞≤B.
等价向量形式 :构造分块反循环矩阵 m = ( ℓ × n ) m=(\ell \times n) m=(ℓ×n)
A = [ circ ‾ ( a 1 ) ∣ ⋯ ∣ circ ‾ ( a ℓ ) ] n × m \boldsymbol{A} = [\overline{\text{circ}}(\boldsymbol{a}1) \mid \cdots \mid \overline{\text{circ}}(\boldsymbol{a}\ell)]{n\times m} A=[circ(a1)∣⋯∣circ(aℓ)]n×m,求非零短向量 z ∈ [ − B , B ] m \boldsymbol{z}\in[-B,B]^m z∈[−B,B]m 使 A z ≡ 0 ( m o d q ) \boldsymbol{A}\boldsymbol{z} \equiv 0 \pmod{q} Az≡0(modq)。
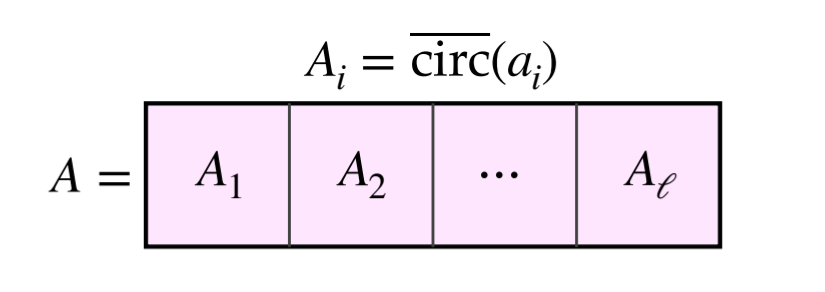
Lyubashevsky和Micciancio证明,求解平均情况 下的环-SIS( Ring-SIS \text{Ring-SIS} Ring-SIS)问题,至少与求解最坏情况 下反循环格的 γ \gamma γ-最短向量问题( SVP γ \text{SVP}_\gamma SVPγ)一样困难。
应用:

5. Ring-LWE
2010年由Lyubashevsky、Peikert和Rosen提出
Ring-LWE ( n , k , q , B ) (n, k, q, B) (n,k,q,B)安全参数: n n n(通常为2的幂,即 n = 2 w n=2^w n=2w),实例数量 k k k,模数 q q q,误差界 B B B(满足 B ≪ q / 2 B \ll q/2 B≪q/2)
定义
给定 a 1 , ... , a k ∈ R q = Z q [ x ] / ( x n + 1 ) a_1, \dots, a_k \in R_q = \mathbb{Z}q[x]/(x^n + 1) a1,...,ak∈Rq=Zq[x]/(xn+1)和 b 1 , ... , b k ∈ R q b_1, \dots, b_k \in R_q b1,...,bk∈Rq,其中 b i = a i s + e i b_i = a_i s + e_i bi=ais+ei( s , e i s, e_i s,ei为"短多项式",即系数均在 [ − B , B ] [-B, B] [−B,B]中)。找到秘密多项式 s ∈ R q s \in R_q s∈Rq,使得对所有 i = 1 , ... , k i=1,\dots,k i=1,...,k,均满足:
b i ≡ a i s + e i ( m o d q ) , ∥ s ∥ ∞ ≤ B s , ∥ e i ∥ ∞ ≤ B e . b_i \equiv a_i s + e_i \pmod{q}, \quad \|s\|\infty \leq B_s, \quad \|e_i\|_\infty \leq B_e. bi≡ais+ei(modq),∥s∥∞≤Bs,∥ei∥∞≤Be.
等价向量形式
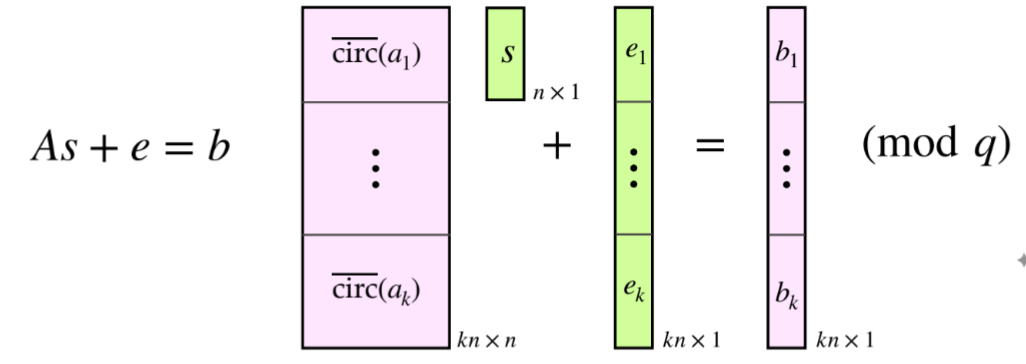
构造分块反循环矩阵:
A = [ circ ‾ ( a 1 ) circ ‾ ( a 2 ) ⋮ circ ‾ ( a k ) ] k n × n \boldsymbol{A} = \begin{bmatrix} \overline{\text{circ}}(\boldsymbol{a}_1) \\ \overline{\text{circ}}(\boldsymbol{a}_2) \\ \vdots \\ \overline{\text{circ}}(\boldsymbol{a}k) \end{bmatrix}{kn \times n} A= circ(a1)circ(a2)⋮circ(ak) kn×n
其中 circ ‾ ( a i ) \overline{\text{circ}}(\boldsymbol{a}_i) circ(ai)是 a i \boldsymbol{a}_i ai的反循环矩阵( n × n n \times n n×n)。则问题等价于求解 n n n维向量 s \boldsymbol{s} s和 k n kn kn维误差向量 e ∈ [ − B , B ] k n \boldsymbol{e} \in [-B, B]^{kn} e∈[−B,B]kn,使得:
A s + e ≡ b ( m o d q ) \boldsymbol{A} \boldsymbol{s} + \boldsymbol{e} \equiv \boldsymbol{b} \pmod{q} As+e≡b(modq)
( b \boldsymbol{b} b是 b 1 , ... , b k b_1, \dots, b_k b1,...,bk的系数向量拼接而成的 k n kn kn维向量)。
安全归约
Lyubashevsky、Peikert和Rosen证明:求解平均情况 下的Ring-LWE问题,至少与量子算法求解最坏情况 下反循环格的 γ \gamma γ-最短整数向量问题( SIVP γ \text{SIVP}_\gamma SIVPγ)一样困难。
目前尚未发现利用矩阵 A \boldsymbol{A} A的结构(反循环性)加速求解的攻击,其安全性与一般LWE相当,但效率更高。
应用:
